Тема № 1 Методи побудови моделей парної лінійної регресії.

Зміст.

1. Загальне поняття про модель парної лінійної регресії.

2. Оцінка невідомих параметрів моделі парної лінійної регресії методом найменших квадратів.

3. Вираження невідомих параметрів моделі парної лінійної регресії через числові характеристики показника та фактора.

4. Оцінка щільності взаємоз язку між показником та фактором. Коефіцієнт кореляції. Властивості.

5. Оцінка щільності взаємозв язку між показником та фактором та перевірка побудованої моделі парної лінійної регресії на адекватність реальній дійсності. Коефіцієнт детермінації та індекс кореляції. Властивості.

6. Перевірка побудованої моделі парної лінійної регресії на адекватність реальній дійсності за F- критерієм Фішера.

7. Вивчення відсоткового впливу фактора на показник. Коефіцієнт еластичності.

8. Оцінка статистичної важливості невідомих параметрів побудованої моделі парної лінійної регресії та побудова для них інтервалів довіри.

9. Моделі нелінійної парної регресії та методи їх зведення до лінійного вигляду.

1. Загальне поняття про модель парної лінійної регресії.

Економетрія – фундаментальна економіко-математична дисципліна, яка на основі статистичних даних про соціально-економічні явища та процеси вивчає методику побудови економетричних моделей. За допомогою цих моделей відображаються кількісні зв'язки, закономірності розвитку, динаміка розглядуваних процесів в економічному просторі. Побудова цих моделей здійснюється з метою прогнозування, аналізу взаємного впливу явищ та прийняття оптимальних управлінських рішень. Об'єктами при побудові економетричних моделей є економічні показники які характеризують досліджувані соціально-економічні явища та процеси та фактори що впливають на показник.

В задачах економетрії необхідно на основі статистичних даних побудувати математичну форму закону зміни одного явища під впливом іншого і провести відповідне її дослідження. Цю математичну форму і називають економетричною моделлю.

Найбільш простими і вживаними економетричними моделями є моделі парної лінійної регресії.

Моделлю парної лінійної регресії називають модель. Яка встановлює лінійну залежність між двома змінними. При цьому одну із змінних називають залежною (показник) і розглядають як лінійну функцію від іншої змінної , яку називають незалежною (фактор).У загальному модель парної лінійної регресії записують так:

(1),

тут - показник, вектор спостережень за залежною змінною - кількість спостережень, - фактор, вектор спостережень за незалежною змінною ,

- невідомі параметри моделі,відшукання (оцінка) яких є основним завданням процесу побудови моделей парної лінійної регресії, - випадкова величина, вектор спостережень вигляду .

Модель (1) прийнято розглядати як суму двох складових:

1. - регресія – характеризує середнє (розрахункове) значення показника для заданого значення фактора, .

2. -з моделі (1), або - відхилення статистичних даних показника від його розрахункових значень.

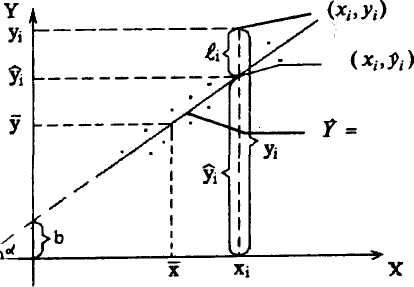
Оскільки, основним завданням побудови моделей парної лінійної регресії є оцінка їх невідомих параметрів, то, для означення критерію а. отже, і методу знаходження розглянемо геометричну інтерпретацію кожної із складових моделі (1)(рис.1).

1. Кожна пара значень незалежної і залежної змінних задається в декартовій системі координат точкою .

2. Регресія задає сукупність прямих , що проходять через точки .

3. - ордината точки перетину прямої з віссю і називають даний параметр перетином регресії.

4. - тангенс кута нахилу прямої до осі і називають даний параметр нахилом регресії.

5. - відстань між точками та : .

Виходячи з цього для знаходження параметрів парної лінійної регресії в декартовій системі координат серед прямих необхідно знайти таку, яка б найкращим чином проходить через множину точок . Досягається це шляхом мінімізації суми квадратів відхилень статистичних даних показника від його розрахункових значень . Цей критерій і покладено в основу методу оцінки невідомих параметрів моделі парної лінійної регресії – методу найменших квадратів.