3.9.1 Баланс мощности при стационарной генерации

Изменение интенсивности излучения, которое распространяется в среде, происходит вследствие поглощения и усиления света за счет вынужденных переходов, а также поглощения или рассеяния на примесях и неоднородностях. Чтобы это отразить запишем закон Бугера так:

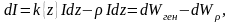
где 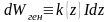– мощность, которая генерируется элементом активной среды длиной 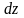, a – мощность, которая поглощается примесями и рассеивается неоднородностями в этом же элементе. Согласно закону сохранения энергии

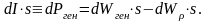
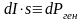есть потери мощности за счет выхода излучения за пределы генерирующего объема с сечением 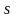и длиной . Для расчета сначала вычислим и .

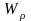3.9.2 Мощность, генерируемая активной средой

Если свет распространяется вдоль стержня активной лазерной среды длиной 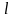и сечением , то

                  (3.26)

Значение 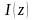найдем из (3.24)

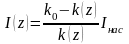
и, подставив в (3.26), получим:

Поскольку коэффициент усиления 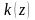зависит от интенсивности потока, то в этих соотношениях он зависит от координаты , вдоль которой распространяется свет. Коэффициент усиления слабого сигнала , будучи характеристикой активной лазерного среды и мощности накачки, не зависит от координаты , если созданы условия его однородного возбуждения. Допустим, что это так. Тогда запишем:

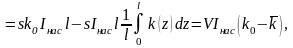                              (3.27)

где учтено, что – объем лазерной среды, – среднее значение коэффициента усиления в активной среде, из теоремы о среднем.

Анализируя соотношение (3.27) видно, что необязательно знать распределение коэффициента усиления вдоль активного стержня. Необходимо каким-то образом определить его среднее значение. Обратим внимание на одну в некотором роде странную особенность: чем больше средний коэффициент усиления 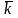, тем меньше генерируемая мощность. Этот парадокс мы выясним чуть позже.