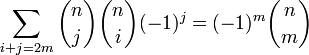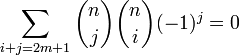- •10. Принцип включения и исключения. Теорема о числе элементов, не обладающих ни одним из указанных свойств (вес каждого элемента равен единице). Доказательство.
- •11. Принцип включения и исключения. Теорема о сумме весов элементов, не обладающих ни одним из заданных свойств. Доказательство.
- •12. Принцип включения и исключения. Теорема о числе элементов, обладающих в точности r-свойствами из n–множества свойств. Доказательство.
- •13. Задача о беспорядках. Теорема о числе беспорядков из элементов n–множества. Доказательство. Следствия.
- •15 Функция Эйлера
- •Функция Мебиуса
- •Число сочетаний с повторениями
- •4. Проверка начальных условий с помощью полученной формулы.
- •Биекция
- •Определение
- •Примеры
- •Свойства
- •Применения в информатике
- •27) Числа Каталана
- •28) Биномиальный коэффициент
- •Явные формулы
- •Треугольник Паскаля
- •Свойства Производящие функции
- •Делимость
- •Тождества
- •Асимптотика и оценки
- •Алгоритмы вычисления
Тождества
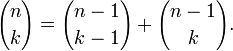
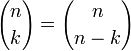 (правило
симметрии).
(правило
симметрии).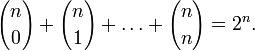
Следствия тождества
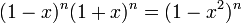 :
:
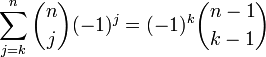 для
для
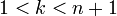 .
.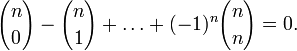 Это
тождество можно усилить
Это
тождество можно усилить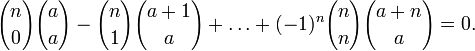 0<a<n
0<a<n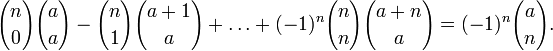 a>=n
a>=n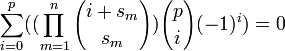 если
если
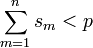 —
более общий вид тождества выше.
—
более общий вид тождества выше.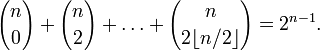
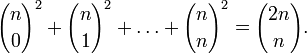
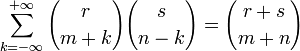 (свёртка
Вандермонда).
(свёртка
Вандермонда).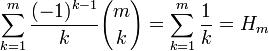 —
m-ое гармоническое
число.
—
m-ое гармоническое
число.Мультисекция ряда даёт тождество, выражающее сумму биномиальных коэффициентов с произвольным шагом s и смещением t
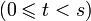 в
виде замкнутой суммы из s слагаемых:
в
виде замкнутой суммы из s слагаемых:
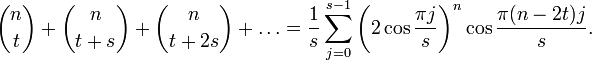
Асимптотика и оценки
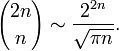
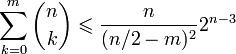 при
при
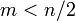
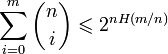 ,
при
,
при
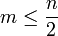
где
![]()
Алгоритмы вычисления
Биномиальные коэффициенты могут быть
вычислены с помощью формулы
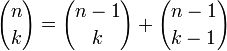 ,
если на каждом шаге хранить значения
,
если на каждом шаге хранить значения
![]() при
при
![]() .
Этот алгоритм особенно эффективен, если
нужно получить все значения
при
фиксированном
.
Этот алгоритм особенно эффективен, если
нужно получить все значения
при
фиксированном
![]() .
Алгоритм требует
.
Алгоритм требует
![]() памяти
(
памяти
(![]() при вычислении всей таблицы биномиальных
коэффициентов) и
времени
(в предположении, что каждое число
занимает единицу памяти и операции с
числами выполняются за единицу времени).
при вычислении всей таблицы биномиальных
коэффициентов) и
времени
(в предположении, что каждое число
занимает единицу памяти и операции с
числами выполняются за единицу времени).
При фиксированном значении k
биномиальные коэффициенты могут быть
вычислены по рекуррентной формуле
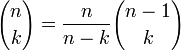 с
начальным значением
с
начальным значением
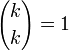 .
Для вычисления значения
этот
метод требует
.
Для вычисления значения
этот
метод требует
![]() памяти
и
времени.
памяти
и
времени.