Биекция

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 февраля 2012; проверки требуют 2 правки.

Перейти к: навигация, поиск

Биективная функция.

Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.

Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы.

Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества).

Определение

Функция называется биекцией (и обозначается ), если она:

1. Переводит разные элементы множества в разные элементы множества (инъективность). Иными словами,

   • .

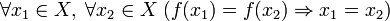2. Любой элемент из имеет свой прообраз (сюръективность). Иными словами,

   • .

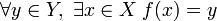Примеры

• Тождественное отображение 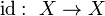 на множестве биективно.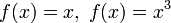

•  — биективные функции из 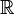в себя. Вообще, любой моном одной переменной нечетной степени является биекцией из в себя.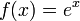

•  — биективная функция из в .

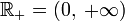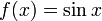• не является биективной функцией, если считать её определённой на всём .

Свойства

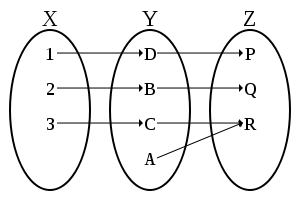
Композиция инъекции и сюръекции, дающая биекцию.

• Функция является биективной тогда и только тогда, когда существует обратная функция 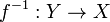такая, что

и

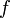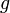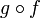• Если функции и биективны, то и композиция функций биективна, в этом случае 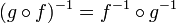. Коротко: композиция биекций является биекцией. Обратное, однако, неверно: если биективна, то мы можем утверждать лишь, что инъективна, а сюръективна.

Применения в информатике

Организация связи «один к одному» между таблицами реляционной БД на основе первичных ключей.

27) Числа Каталана

Материал из Википедии — свободной энциклопедии

Перейти к: навигация, поиск

Числа Катала́на — числовая последовательность, встречающаяся во многих задачах комбинаторики. Последовательность названа в честь бельгийского математика Каталана, хотя была известна ещё Л. Эйлеру.

Первые несколько чисел Каталана:

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, … (последовательность A000108 в OEIS)

Содержание

Определения

n-е число Каталана можно определить одним из следующих способов:

• Количество разбиений выпуклого (n+2)-угольника на треугольники непересекающимися диагоналями.

• Количество правильных скобочных последовательностей длины 2n, то есть таких последовательностей из n левых и n правых скобок, в которых количество открывающих скобок равно количеству закрывающих, и в любом её префиксе открывающих скобок не меньше, чем закрывающих.

Например, для n=3 существует 5 таких последовательностей:

((())), ()(()), ()()(), (())(), (()())

то есть .

• Количество способов соединения 2n точек на окружности n непересекающимися хордами.

• Количество неизоморфных упорядоченных бинарных деревьев с корнем и n+1 листьями.

Свойства

• Числа Каталана удовлетворяют рекуррентному соотношению:

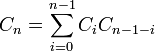и для

Это соотношение легко получается из того, что любая непустая правильная скобочная последовательность однозначно представима в виде w=(w₁)w₂, где w₁, w₂ — правильные скобочные последовательности.

• Производящая функция чисел Каталана равна:

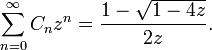
• Числа Каталана можно выразить через биномиальные коэффициенты:

Другими словами, число Каталана равно разности центрального биномиального коэффициента и соседнего с ним в той же строке треугольника Паскаля.

• Асимптотически

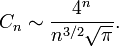
Чтобы не ограничиваться одной только ссылкой, напишу приведенный в "Конкретной математике" вывод формулы для чисел Каталана. Красивое и очень простое рассуждение. Определение (одно из многих). Числом Каталана C_n называется количество последовательностей длины (2n+1) a₀, a₁, ..., a_2n, составленных из +1 и -1, таких что сумма чисел равна +1, а все частичные суммы a₀, a₀+a₁, ..., a₀+...+a_2n положительны. Лемма Рени. Если x₁, x₂, ..., x_m - любая последовательность целых чисел, сумма которых равна +1, то ровно у одного из её циклических сдвигов x₁, x₂, ..., x_m x₂, ..., x_m, x₁ x_m, x₁, ..., x_m-1 частичные суммы все положительны. Доказательство. Продолжим последовательность периодически до бесконечной последовательности: x_m+k=x_k, для всех k>0. Если для этой бесконечной последовательности нарисовать график частичных сумм s_n=x₁+...+x_n, то он будет иметь "средний наклон" 1/m, поскольку s_n+m=s_n+1. Весь график может быть заключён между двумя прямыми наклона 1/m. Эти прямые касаются графика ровно один раз на каждом периоде из m точек, поскольку прямые с наклоном 1/m могут проходить через точки с целыми координатами только один раз на m единиц. Единственная нижняя точка касания -- это то единственное место в цикле, начиная с которого все частные суммы будут положительны. Подсчёт последовательностей из +1 и -1 с общей суммой +1. Всего есть C_2n+1ⁿ последовательностей, содержащих n элементов -1 и (n+1) элементов +1. Построим все C_2n+1ⁿ последовательностей и все (2n+1) их циклических сдвигов в виде таблицы из C_2n+1ⁿ строк и (2n+1) столбцов. Очевидно, что каждая последовательность встречается в таблице (2n+1) раз, по одному разу в каждом столбце. По лемме Рени в каждой строке содержится ровно одна последовательность с положительными частичными суммами. Таким образом, всего в таблице искомые последовательности встречается C_2n+1ⁿ раз. Каждая встречается (2n+1) раз. Следовательно C_n = C_2n+1ⁿ/(2n+1) = C_2nⁿ/(n+1).