
- •10. Принцип включения и исключения. Теорема о числе элементов, не обладающих ни одним из указанных свойств (вес каждого элемента равен единице). Доказательство.
- •11. Принцип включения и исключения. Теорема о сумме весов элементов, не обладающих ни одним из заданных свойств. Доказательство.
- •12. Принцип включения и исключения. Теорема о числе элементов, обладающих в точности r-свойствами из n–множества свойств. Доказательство.
- •13. Задача о беспорядках. Теорема о числе беспорядков из элементов n–множества. Доказательство. Следствия.
- •15 Функция Эйлера
- •Функция Мебиуса
- •Число сочетаний с повторениями
- •4. Проверка начальных условий с помощью полученной формулы.
- •Биекция
- •Определение
- •Примеры
- •Свойства
- •Применения в информатике
- •27) Числа Каталана
- •28) Биномиальный коэффициент
- •Явные формулы
- •Треугольник Паскаля
- •Свойства Производящие функции
- •Делимость
- •Тождества
- •Асимптотика и оценки
- •Алгоритмы вычисления
Функция Мебиуса
Функция Мебиуса (n), где n – натуральное число, принимает следующие значения:

Функция Мебиуса позволяет записать функцию Эйлера в виде суммы:
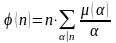 .
.
Суммирование идет по всем делителям n (а не только по простым делителям).
Пример. Вычислим φ(100), используя функцию Мебиуса.
Все делители 100 – {1, 2, 4, 5, 10, 20, 25, 50, 100}.
(1) = 1,
(2) = (-1)1 = -1 (у двойки один простой делитель – 2)
(4) = 0 (4 делится на квадрат двойки)
(5) = (-1)1 = -1 (у 5 один простой делитель – 5)
(10) = (-1)2 = 1 (у 10 два простых делителя – 2 и 5)
(20) = 0 (20 делится на квадрат двойки)
(25) = 0 (25 делится на квадрат пятерки)
(50) = 0 (50 делится и на 22, и на 55)
(100) = 0 (100 делится и на 22, и на 55)
Таким образом,
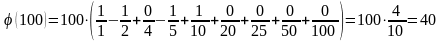
Свойство функции Мебиуса:
 .
.
Например, n=100, {1, 2, 4, 5, 10, 20, 25, 50, 100}.
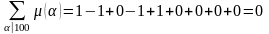 .
.
16 Теорема о числе способов выбора k-элементов, среди которых нет двух соседних, из n элементов, расположенных в ряд. Доказать с помощью получения рекуррентной формулы.
17
Число сочетаний с повторениями
Число r-сочетаний с повторениями из n-множества равно
.
– доказательство с помощью рекуррентной формулы.
Метод базируется на получении формулы, позволяющей вычислять значения искомой величины шаг за шагом, исходя из известных начальных значений и значений, вычисленных на предыдущих шагах.
Рекуррентная формула r-го порядка – формула вида
an= f(n, an-1, an-2, … , an-r).
Формула выражает при n>r каждый член последовательности {ai} через предыдущие r членов. Построение рекуррентной формулы состоит из следующих шагов.
1. Выработка начальных условий исходя из каких-либо очевидных соотношений.
Обозначим
 через f(n,r). Очевидно, что
через f(n,r). Очевидно, что
 (1)
(1)
2. Логические рассуждения. Зафиксируем какой-либо элемент во множестве S. Тогда относительно любого r-сочетания с повторениями из n-множества S можно сказать, содержит ли оно данный зафиксированный элемент или нет.
Если содержит, то остальные (r-1) элемент можно выбрать f(n, r-1) способами.
Если не содержит (в выборке этого элемента нет), то r-сочетание составлено из элементов (n-1)-множества (множество S за исключением данного зафиксированного элемента). Число таких сочетаний f(n-1, r).
Т.к. эти случаи взаимоисключающие, то по правилу суммы
 (2)
(2)
3. Проверка формулы на некоторых значениях и вывод общей закономерности.
1) Вычислим f(n,0). Из (2) следует
 . (3)
. (3)
Тогда f(n,0)=f(n,1)-f(n-1,1). Из (1) f(n,1)=n, f(n-1,1)=n-1.
Следовательно, f(n,0)=n-(n-1)=1= .
.
2) f(n,1) = f(n,0)+f(n-1,1)
= 1+n-1 = n =
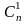 =
=
 .
.
3) f(n,2) = f(n,1)+f(n-1,2) = n+f(n-1,1)+f(n-2,2) = n+(n-1)+f(n-2,1)+f(n-3,2) = … =
= n+(n-1)+…+2+1 =

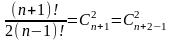 .
.
(сумма арифметической прогрессии)
4) f(n,3) = f(n,2)+f(n-1,3)
=
 +f(n-1,2)+f(n-2,3)
=
+
+f(n-1,2)+f(n-2,3)
=
+ +f(n-2,2)+f(n-3,3)
= … =
+f(n-2,2)+f(n-3,3)
= … =
 .
.
(сумма геометрической прогрессии)
5) f(n,4) =

На основе частных случаев можно предположить, что

4. Проверка начальных условий с помощью полученной формулы.
 ,
,
что согласуется с (1) #
19, 20) Число бинарных деревьев с n вершинами равно C(n), где C(n) – это n-ое число Каталана.
Количество бинарных деревьев из n вершин называется числом Каталана, которое обладает множеством интересных свойств. N-ое число Каталана считается по формуле (2n)! / (n+1)!n!, которая растёт экспоненциально. (В Википедии предложено несколько доказательств, что это форма числа Каталана.) Число бинарных деревьев данного размера 0 1 1 1 2 2 4 14 8 1430 12 208012 16 35357670
Подстановка
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Это статья о подстановке как о синтаксической операции над термами. Возможно, вас интересует перестановка.
В математике и компьютерных науках подстановка — это операция синтаксической замены подтермов данного терма другими термами, согласно определённым правилам. Обычно речь идёт о подстановке терма вместо переменной.
Содержание
|
Определения и обозначения
Для подстановки не существует
универсальной, согласованной нотации,
равно как и стандартного определения.
Понятие подстановки варьируется не
только в рамках разделов, но и на уровне
отдельных публикаций. В целом, можно
выделить контекстную подстановку
и подстановку «вместо». В первом
случае место в терме, где происходит
замена, задаётся контекстом, то есть
частью терма, «окружающим» это место.
В частности, такое понятие подстановки
используется в переписывании.
Второй вариант более распространён. В
этом случае подстановка обычно задаётся
некоторой функцией
![]() из
множества переменных в множество термов.
Для обозначения действия подстановки,
как правило, используют постфиксную
нотацию. Например,
из
множества переменных в множество термов.
Для обозначения действия подстановки,
как правило, используют постфиксную
нотацию. Например,
![]() означает
результат действия подстановки
означает
результат действия подстановки
![]() на
терм
на
терм
![]() .
.
В подавляющем большинстве случаев
требуется чтобы подстановка имела
конечный носитель, то есть, чтобы
множество
![]() было
конечным. В таком случае её можно задать
простым перечислением пар
«переменная-значение». Поскольку
каждую такую подстановку можно свести
к последовательности подстановок,
замещающих всего по одной переменной
каждая, не ограничивая общности можно
считать, что подстановка задаётся одной
парой «переменная-значение», что
обычно и делается.
было
конечным. В таком случае её можно задать
простым перечислением пар
«переменная-значение». Поскольку
каждую такую подстановку можно свести
к последовательности подстановок,
замещающих всего по одной переменной
каждая, не ограничивая общности можно
считать, что подстановка задаётся одной
парой «переменная-значение», что
обычно и делается.
Последнее определение подстановки является, видимо, самым типичным и часто используемым. Однако и для него не существует единой общепринятой нотации. Наиболее часто для обозначения подстановки a вместо x в t используется запись t[a/x], t[x:=a] или t[x←a].
Подстановка переменной в λ-исчислении
В λ-исчислении, подстановка определяется
структурной индукцией. Для произвольных
объектов
![]() ,
,
![]() и
произвольной переменной
и
произвольной переменной
![]() результат
замещения произвольного свободного
вхождения
в
считается
подстановкой и определяется индукцией
по построению
:
результат
замещения произвольного свободного
вхождения
в
считается
подстановкой и определяется индукцией
по построению
:
(i) базис:
![]() :
объект
совпадает
с переменной
.
Тогда
:
объект
совпадает
с переменной
.
Тогда
![]() ;
;
(ii) базис:
![]() :
объект
совпадает
с константой
:
объект
совпадает
с константой
![]() .
Тогда
.
Тогда
![]() для
произвольных атомарных
для
произвольных атомарных
![]() ;
;
(iii) шаг:
![]() :
объект
неатомарный
и имеет вид аппликации
:
объект
неатомарный
и имеет вид аппликации
![]() .
Тогда
.
Тогда
![]() ;
;
(iv) шаг:
![]() :
объект
неатомарный
и является
-абстракцией
:
объект
неатомарный
и является
-абстракцией
![]() .
Тогда [
.
Тогда [![]() ;
;
(v) шаг:
![]() :
объект
неатомарный
и является
:
объект
неатомарный
и является
![]() -абстракцией
-абстракцией
![]() ,
причем
,
причем
![]() .
Тогда:
.
Тогда:
![]() для
и
для
и
![]() или
или
![]() ;
;
![]() для
и
для
и
![]() и
и
![]() .
.
Подстановка переменной в программировании
Подстановка переменной (англ. substitution) в аппликативном программировании понимается следующим образом. Для вычисления значения функции f на аргументе v применяется запись f(v)}, где f определена конструкцией f(x) = e. Запись f(v) в этом случае означает, что в выражении e происходит замещение, или подстановка переменной x на v. Выполнение замещения происходит в соответствии с семантикой вычислений.
Подстановка переменной (англ. assignment) в программировании понимается как присваивание. Оператор присваивания является проявлением эффекта «бутылочного горлышка» фон Нейманна для традиционных языков программирования[1]. От этого свободны аппликативные вычислительные системы.
http://math.nsc.ru/LBRT/u3/bard/fails/Brenner_Evans.pdf
21 Производящие функции. Производящая функция (нумератор) и перечисляющая производящая функция для сочетаний без повторений.
Производящие
функции: 1)Z-преобразования
2)генератриса 3)порождающая функция
4)производящая функция последовательности
{ar}
на базисе {gr}
– функция f
при разложении которой в ряд по функциям
фиксированного базиса {gr}
образуется данная последовательность
коэффициентов {ar}
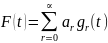 …………*)
…………*)
Данный ряд – формальный. Название формальный означает, что мы формулу *) трактуем как удобную запись нашей последовательности – в данном случае несущественно, для каких (действ и комплексных) значений он сходится. Роль t сводится к тому чтобы различать коэффициенты последовательности А0,А1,…Аr….поэтому в теории производящих функций никогда не вычисляют значения таого ряда для конкретного значения переменной t. Выполняются лишь только некоторые операции на таких рядах, а затем определяются только некоторые операции на таких рядах а затем определяются коэффициенты при отдельных степенях переменной t.
Обычно в качестве
22Производящая функция. Производящая функция (нумератор) и перечисляющая производящая функция для сочетаний с повторениями.
Производящая
ф-я для
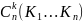 :
:
Правило построения
1)Если
эл-т типа i
может входить в сочетания K1
или K2
или… Ki
раз, то ему
соотв множитель

2)F(t)=
3)Остается
найти коэф. при
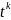
экспоненциальная производящая ф-я для размещений правило построения
Если ai множитель входящий в размещения К1 или…или Кi раз, то ему соответствует множитель
 если надо найти число размещений
если надо найти число размещений
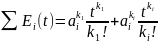 , если надо найти сами размещения
, если надо найти сами размещенияE(t)=

Остается найти коэф при
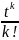
25) К комбинаторным числам также относятся числа Стирлинга первого и второго рода. Эти числа определяются как коэффициенты в равенствах
,
и имеют простой комбинаторный смысл — равно числу элементов группы подстановок являющихся произведениями ровно k непересекающихся циклов, а равно числу разбиений n-элементного множества на k непустых подмножеств. Очевидно, что . Аналогичная сумма чисел Стирлинга второго рода называется n-м числом Белла и равна числу всех разбиений n-элементного множества. Для чисел Белла справедлива рекуррентная формула .
При решении комбинаторных задач часто оказывается полезна формула включений—исключений
,
позволяющая находить мощность объединения множеств, если известны мощности их пересечений. Воспользуемся формулой включений—исключений для получения явной формулы для чисел Стирлинга второго рода.
Числа Стирлинга первого рода
Материал из Википедии — свободной энциклопедии
Перейти к: навигация, поиск
Числа Стирлинга первого рода (без знака) — количество перестановок порядка n с k циклами.
|
Определение
Числами Стирлинга первого рода (со знаком) s(n, k) называются коэффициенты многочлена:
![]()
где (x)n — символ Похгаммера (убывающий факториал):
![]()
Как видно из определения, числа имеют чередующийся знак. Их абсолютные значения задают количество перестановок множества, состоящего из n элементов с k циклами.
Рекуррентное соотношение
Числа Стирлинга первого рода задаются рекуррентным соотношением:
s(n,n) = 1, для n ≥ 0,
s(n,0) = 0, для n > 0,
![]() для
0 < k < n.
для
0 < k < n.
Доказательство.
Для n=1 это равенство проверяется непосредственно. Пусть перестановка (n-1)-го порядка распадается на k циклов. Число n можно добавить после любого числа в соответствующий цикл. Все полученные перестановки — различные и содержат k циклов, их количество (n-1)·s(n-1, k). Из любой перестановки (n-1)-го порядка, содержащей k-1 цикл, можно сформировать единственную перестановку n порядка, содержащую k циклов, добавив цикл образованный единственным числом n. Очевидно, что эта конструкция описывает все перестановки n-го порядка, содержащие k циклов. Тем самым равенство доказано.
Пример
Первые ряды:
n\k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
|
|
|
|
|
|
1 |
0 |
1 |
|
|
|
|
|
2 |
0 |
−1 |
1 |
|
|
|
|
3 |
0 |
2 |
−3 |
1 |
|
|
|
4 |
0 |
−6 |
11 |
−6 |
1 |
|
|
5 |
0 |
24 |
−50 |
35 |
−10 |
1 |
|
6 |
0 |
−120 |
274 |
−225 |
85 |
−15 |
1 |
|
|
|
|
|
|
|
|
В комбинаторике
числом Стирлинга второго рода из n
по k, обозначаемым
![]() или
или
![]() ,
называется количество неупорядоченных
разбиений
n-элементного множества
на k непустых подмножеств.
,
называется количество неупорядоченных
разбиений
n-элементного множества
на k непустых подмножеств.
|
Рекуррентная формула
Числа Стирлинга второго рода удовлетворяют рекуррентному соотношению:
![]() ,
для n ≥ 0,
,
для n ≥ 0,
![]() ,
для n > 0,
,
для n > 0,
![]() для
для
![]()
Явная формула
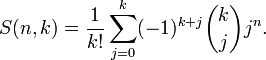
Пример
Начальные значения чисел Стирлинга второго рода приведены в таблице:
n\k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
3 |
0 |
1 |
3 |
1 |
0 |
0 |
0 |
4 |
0 |
1 |
7 |
6 |
1 |
0 |
0 |
5 |
0 |
1 |
15 |
25 |
10 |
1 |
0 |
6 |
0 |
1 |
31 |
90 |
65 |
15 |
1 |
Свойства
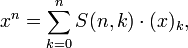 где
где
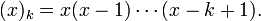
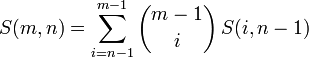
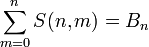 —
число
Белла.
—
число
Белла.
Биективным отображением называется отображение, обладающее признаками инъективности и сюръективности одновременно.
