6. Комбинаторные задачи о покрытиях, укладках, разбиениях. Примеры. Теорема о числе разбиений элементов множества на 2, 3, …,k классов, без учета их порядка в классах и без ограничений на занятость класса. Доказательства. Следствия.

Задача о покрытии

Найти такие множества T_i, i = 1, 2, …, r, чтобы (чтобы объединение этих множеств «покрыло» S). Например, застелить весь пол в комнате несколькими коврами. Ковры могут накладываться друг на друга (множества могут пересекаться), но незакрытых участков поФла быть не должно.

Во многих задачах покрытие должно быть наиболее экономичным (так называемое минимальное покрытие), когда число множеств T_i должно быть минимальным, сами они должны содержать минимально возможное число элементов.

Задача об укладке

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i T_j =  при ij) чтобы (чтобы объединение этих множеств вошло в S).

Например, уложить несколько предметов в одну коробку. Между предметами могут быть пустые промежутки, но сами предметы друг с другом не пересекаются и укладываются в коробку.

Во многих задачах укладка должна быть наиболее экономичной, когда укладывается максимально возможное количество предметов, а количество пустых промежутков должно быть как можно меньше.

Задача о разбиении

Найти такие попарно непересекающиеся множества T_i, i = 1, 2, …, r, (T_i T_j =  при ij) чтобы 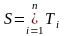(чтобы объединение этих непересекающихся множеств дало S).

Например, группы в институте – это разбиение множества студентов института. Группы не пересекаются, а их объединение дает множество всех студентов института.

Теорема о числе разбиений элементов множества на 2, 3, …,k классов, без учета их порядка в классах и без ограничений на занятость класса.

Теорема заключается в том, что данное число равно:

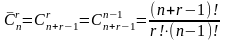
В лекции давалась задача о кольцах (сколькими способами можно одеть на пальцы одной руки 7 колец). Вот нечто подобное с доказательством:

Есть k ящиков и n>=k однаковых шаров. Сколькими способами можно разложить шары по ящикам, если могут быть пустые ящики?

Решение

Давайте определять раскладку так: выложим шары в ряд и поставим между ними k-1 перегородку. То, что слева от первой перегородки, положим в первый ящик, между первой и второй - во второй... то, что справа от последней - в последний, k-й ящик. Ящик будет пустым, только если две перегородки стоят рядом не разделенные шарами, либо перегородка стоит с краю, левее или правее всех шаров. Шары и перегородки можно ставить в произвольном порядке. Давайте считать, что у нас расставлено в ряд n+k-1 объектов: n из них шары, а остальные - перегородки. Тогда раскладка будет определяться тем, на каких местах какие объекты стоят. Из n+k-1 мест можно выбрать n мест для шаров Cn+k-1n способами, или: k-1 место для перегородок Cn+k-1k-1 способами. Эти числа равны и оба являются ответом.

7. Комбинаторные задачи о покрытиях, укладках, разбиениях. Примеры. Теорема о числе разбиений элементов множества на 2, 3, …, k классов, с учетом их порядка в классах и без ограничений на занятость класса. Доказательства. Следствия.

… смотри предыдущий вопрос

Теорема (PS лекции Гусева)

Пусть мы рассматриваем упорядоченные разбиения n-множества на k-подмножеств T_i.

(R_1, R_2,…,R_k) полиноминальные коэффициенты

Доказательство

Следствие

R сочетаний без повторений из n множества можно интерпретировать как (R, n-R)

Пример: разбиение «Комбинаторика»

К 2

О 2

М 1

Б 1

И 2

Н 1

А 2

Т 1

О

Р 1

И

К

А

Р₁₃ (221121121)=13!/2!2!1!...1!

8.9 Интерпретация комбинаторных операций выборки и упорядочивания как отображения множеств. Примеры. Сформулировать и доказать теорему о числе различных отображений N в K. Условие существования взаимно-однозначных отображений.

Интерпретация комбинаторных операций

Интерпретация и выборкаиз k множества является заполнение ящиков из совокупности n с учетом k.

Надо формализовать:

1. Вид элементов и их число

2. Вид ящиков и их вместимость

3. Порядок элементов, помещенных в ящик

4. Порядок ящиков

Определение. Пусть А и В – произвольные множества. Отображением множества А в множество В называют правило (соответствие), которое каждому элементу множества А ставится в соответствие единственный для этого элемента элемент множества В.

Инъективные, сюръективные, биективные отображения

О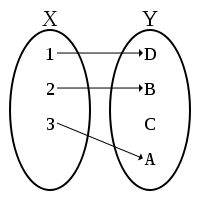 тображение   называется: 

инъективным, если разные элементы множества   переводятся в разные элементы множества  . 

Инъективное отображение удобно представлять как раскладывание m помеченных шаров в n различных ящиков так, чтобы в каждом ящике было не более одного шара.

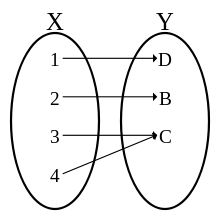  сюръективным, если каждый элемент множества   имеет хотя бы один прообраз во множестве   при отображении  .

сюръективное отображение удобно представлять как раскладывание m помеченных шаров в n различных ящиков так, чтобы в в каждом ящике был хотя бы 1элемент.

 биективным (взаимно-однозначным отображением), если  каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. 

Биекция  — это отображение, которое является одновременно и сюръективным, и инъективным.

10. Принцип включения и исключения. Теорема о числе элементов, не обладающих ни одним из указанных свойств (вес каждого элемента равен единице). Доказательство.

Пусть дано n-множество элементов S и N-множество свойств p₁,…,p_N. Элементы множества S могут как обладать, так и не обладать любым из свойств p_i. Количество элементов, обладающих теми или иными свойствами и их комбинациями, известно.

Требуется найти число элементов, не обладающих ни одним из свойств.

Обозначим:

1. через некоторую i-ю выборку свойств, а через – число элементов, каждый из которых обладает всеми этими r выбранными свойствами.

2. через – отсутствие у элемента свойства p_i. Тогда, например, – число элементов, обладающих свойствами p₁ и p₃ и не обладающих свойствами p₂ и p₄.

Рассмотрим два частных случая.

1. Имеется лишь одно свойство p. Тогда очевидно, что число элементов, не обладающих свойством p, равно общему числу элементов минус число элементов, обладающих свойством p. .

2. Имеется конечное множество свойств p₁,…,p_N, но они не совместимы (т.е. ни один из элементов не может обладать более чем одним свойством). Тогда число элементов, не обладающих ни одним из свойств, равно общему числу элементов минус число элементов, обладающих свойством p₁, минус число элементов, обладающих свойством p₂ и т.д.

.

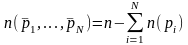Общий случай – элементы могут обладать комбинацией совместимых свойств.

Теорема. Если даны n-множество элементов S и N свойств p_i , то число элементов, не обладающих ни одним из свойств, равно (формула решета):

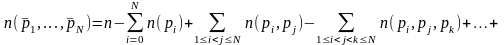
n

n(p₁) n(p₂)

n(p₃)

Рассмотрим доказательство при N=3.

Обозначим кругами подмножества элементов, обладающих хотя бы свойством p₁, хотя бы свойством p₂ и хотя бы свойством p₃. Тогда пересечения двух кругов будут давать подмножество элементов, обладающих хотя бы двумя свойствами одновременно, а пересечение всех трех кругов дает подмножество элементов, обладающих всеми тремя свойствами. Прямоугольник, в котором расположены круги, обозначает все множество S, содержащее n элементов. Нужно найти количество элементов, не обладающие ни одним из трёх свойств (за пределами кругов).

Чтобы найти это число, нужно из n-множества исключить элементы, обладающие свойством p₁, затем обладающие свойством p₂, затем – p₃, т.е. вычесть . Однако при этом элементы, обладающие двумя свойствами (например, p₁ и p₂), окажутся исключёнными дважды (сначала как элементы, обладающие свойством p₁, затем как обладающие p₂). Следовательно, нужно возвратить по одному разу элементы, исключённые дважды, т.е. добавить 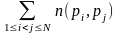. Но при этом элементы, обладающие сразу тремя свойствами (p₁, p₂, p₃), сначала были трижды исключены как элементы, обладающие по отдельности свойствами p₁, p₂ или p₃, а затем трижды включены как обладающие парами свойств. Поэтому их нужно один раз исключить, т.е. вычесть . 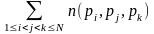Рассуждая подобным образом, получаем алгоритм, который состоит в попеременном включении и отбрасывании подмножеств, дающий приведенную выше формулу решета.

Следствие. Характер доказательства таков, что его можно применять к любой комбинации свойств. Например,

.
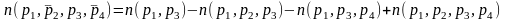