Лабораторная работа № 8 «График занятости»

Цель: на примере классических задач познакомиться с задачами по оптимизации графика занятости и их практической реализацией в MS EXCEL с целью решения с помощью надстройки «Поиск решения».

Программные средства: MS Excel, надстройка Solver (Поиск решения).

График занятости

Постановка задачи

Рассмотрим интересную задачу, связанную с формированием графика занятости персонала.

Парк отдыха обслуживается семью группами сотрудников (группы обозначены А, Б…Ж). Признак разделения на группы – разные выходные дни. Выходных дней для каждой группы – не менее двух, выходные дни следуют подряд. Один сотрудник входит только в одну группу. Известна потребность в сотрудниках в каждый из дней (потребность различна и известна, например, на основе данных о статистически среднем количестве посетителей парка отдыха в каждый из дней недели).

Все сотрудники имеют одинаковый размер недельной оплаты, который не зависит от графика работы.

Необходимо подобрать такую численность сотрудников в каждой группе, чтобы добиться минимизации затрат на оплату труда при выполнении требования по числу сотрудников на каждый день.

Реализация в Excel

Структура рабочего листа График занятости

Диапазон ячеек (ячейка)	Назначение	Примечания
D20	Общая недельная зарплата	Цель решения задачи – уменьшение этой величиной за счёт уменьшения числа сотрудников каждой из групп
D7:D13	Изменяемые данные – число сотрудников каждой из групп	Нужно подобрать такие значения этих ячеек, чтобы значение ячейки D20 было как можно меньше
F17:L13	График работы групп	Единица в этих ячейках означает, что группа в соответствующий день работает, ноль – не работает. Значение (1 или 0) обрабатывается в формулах, находящихся в ячейках F15:L15, в которых подсчитывается общее число сотрудников, работающих в определённый день
F15:L15	Количество сотрудников, работающих в каждый из дней	В каждой из этих ячеек находятся формулы, аналогичные формуле, показанной в строке формул на рис.
F17:L17	Требуемое количество сотрудников в каждый из дней недели	Задаётся значениями (не рассчитывается формулами). Предполагается, что эта потребность основывается на предыдущем опыте работы парка
D15	Общее число сотрудников парка	Рассчитывается формулой =СУММ (D7:D13)

Ограничение задачи оптимизации графика занятости

Ограничение	Примечания
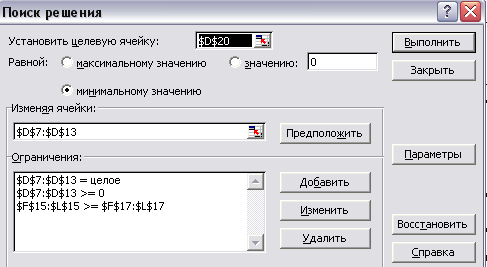
D7:D13>=0	Количество сотрудников в группе не может быть отрицательны, однако может быть равным нулю – это означает, что можно организовать меньшее количество групп (далее мы увидим целый ряд оптимальных решений, в которых в одной или нескольких группах сотрудники не нужны; при этом требование по численности сотрудников на каждый день выполняется).
D7:D13= Целое	Число сотрудников должно быть целым
F15:L15>=F17:L17	Число ежедневно занятых сотрудников не должно быть меньше ежедневной потребности

З апускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить.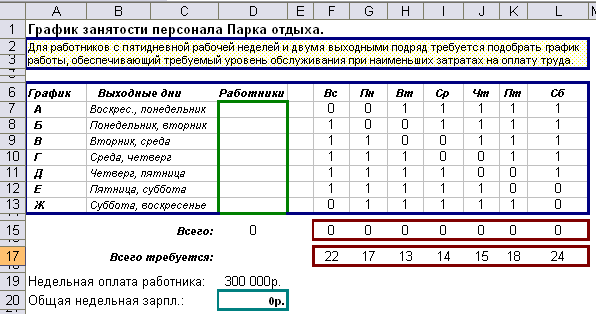

Анализ результатов.

Важной особенностью этой задачи является наличие нескольких оптимальных решений, каждое из которых обеспечивает достижение целевой функции при выполнении всех ограничений.

Таким образом (методом последовательного расчета) можно найти все оптимальные решения и выбрать наиболее подходящее с точки зрения дополнительных критериев (которые не заданы (или не могут быть заданы) в качестве ограничений).

В данном случае, например, вполне целесообразным окажется подбор решения, обеспечивающего большее, чем требуется, общее число сотрудников в наиболее напряженные дни работы парка (резерв сотрудников, работающих в эти дни). Такими днями, очевидно, являются суббота и воскресение.

Все оптимальные решения этой задачи для заданных условий и ограничений, представлены в табл.

Таблица. Численность сотрудников в группах (оптимальные решения задачи оптимизации графика занятости)

Группа сотрудников	Численность сотрудников
А	3	3	3	2	2	3	2	2	3	2
Б	4	4	5	6	6	5	6	6	5	4
В	8	8	7	6	6	7	6	6	6	8
Г	3	3	3	5	5	4	3	4	5	3
Д	7	6	7	5	5	5	7	6	5	7
Е	0	1	0	0	1	1	0	1	1	0
Ж	0	0	0	1	0	0	1	0	0	1

Общее число сотрудников в любом из решений равно25.

Расписание

Постановка задачи.

Расписание касается людей или машин, состояние которых на определенном этапе определяются двумя вариантами – человек в определенный день вышел/ не вышел, машина на определенной стадии работает/не работает т. д. Соответственно, расписание имеет вид комбинаций типу 011100101.

В нашем случае 10 работниц исполняют возложенные на них функции, на каждый день известны потребности в их численности, при чем установлена 5-дневная рабочая неделя. Нужно определить расписание выхода на работу, чтобы удовлетворить эти потребности с минимальным количеством чел./день.

Экономико-математическая модель.

Найти таблицу расписания такую, чтобы общие количество человек было min

При ограничениях:

Всего задействованных человек = Потребностям в них;

Количество рабочих дней каждой работницы = 5,

а также все неизвестные двоичного типа.

Р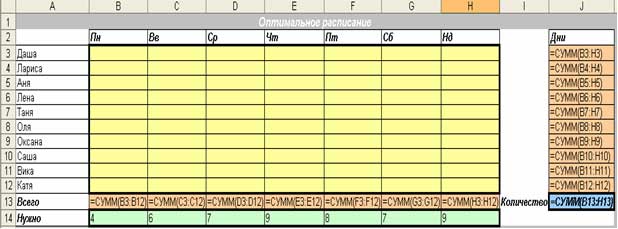 еализация в Excel.

Создаем таблицу с формулами, которые связывают план, ограничения и целевую функцию (Количество):

• в столбец Дни вводим формулу сумы по строкам матрицы расписания;

• в строку Всего вводим формулу сумы по столбцам матрицы расписания;

• в целевую ячейку Количество вводим формулу: =СУММ(Всего).

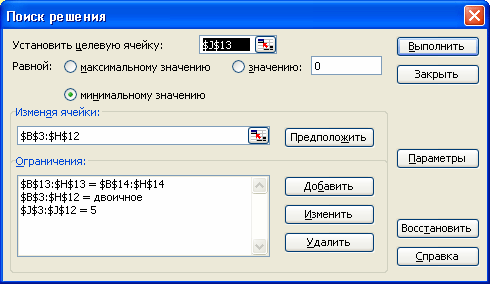
Запускаем программу Поиск решений командой Данные/Анализ/Поиск решения (В Excel 2007) Сервис/Поиск решения (В Excel 2003 и ниже). В полях Установить целевую ячейку, Изменяя ячейки, Ограничения вводим соответствующие адреса ячеек. Так как это линейная модель, то не забываем фиксировать в окне Параметры поиска решений переключатель на позицию Линейная модель и Неотрицательные значения. Нажимаем кнопку Выполнить

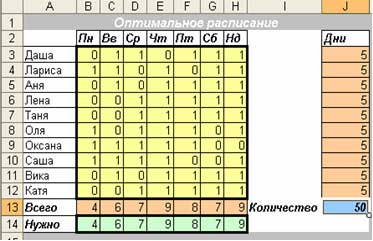
Анализ результатов.

В полученном результате видим, что данное расписание соответствует нашим заданным ограничениям и при котором задействовано наименьшее количество работниц – это значит, что найденный план оптимальный.