3.2. Статистическая оценка параметров распределения

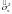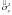Состоятельные и несмещенные оценки основных парамет­ров распределения случайной величины Х (илиY) математиче­ского ожидания m_х (или m_Y) и дисперсии (или ) могут быть получены по формулам:

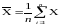; (3.1)

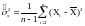, (3.2)

где n — число, определяющее размер выборки.

Оценку коэффициента корреляции между величинами Х и Y определяют по формуле:

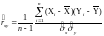(3.3)

Коэффициент корреляции показывает степень связи между переменными величинами. Если r=0, то переменные не коррелируют, а при r=±1 между переменными имеется связь.

Значения 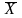и 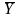рассчитываются по формуле (3.1), а 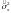и — по формуле (3.2).

Так как оценки (3.1) — (3.3) определяют по выборке ко­нечного размера, возникает вопрос об их статистической дос­товерности и точности.

Обозначим через 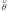оценку интересующего нас параметра. Тогда задача определения достоверности и точности оценки сводится к определению такого интервала (q₁, ₂), включаю­щего параметр _кр, что с вероятностью 1-p (р – уровень значимости, достаточно малая величина, равная 0,1; 0,05; 0,01) можно утверждать, что неизвестное истинное значение параметра находится в этом интервале. Интервал (₁, ₂) называют доверительным интер­валом, а вероятность 1-р — доверительной вероятностью.

Рассмотрим случай, когда величина Х (и Y) имеет нор­мальный закон распределения с плотностью вероятности

.

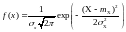Здесь и далее во всех формулах величины Х можно заме­нить на Y.

Доверительный интервал для математического ожидания ( -e_p, +e_p), включающий m_х с вероятностью 1-р, находят из условия

P[ -e_p<m_x< +e_p]=1-p,

которое можно представить в виде

P[| -m_x|<e_p]=1-p. (3.4)

Введем параметр t=[( -m_x)/ 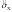]× 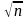, имеющий t-распределение Стьюдента с f = n-1 степенями свободы. Тогда равенство (3.4) перепишется в виде:

P[ | -m_x|<t(p,f) 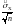]=1-p,

где t(p,f) определяют по таблице распределения Стьюдента (табл. 3.1) при вероятности р и числе степеней свободы f = n-1. Доверительный интервал для m_x, соответствующий довери­тельной вероятности 1-р, есть

[ -t(p,f) , +t(p,f) ]. (3.5)

Чтобы определить доверительный интервал для генераль­ной дисперсии, необходимо найти границы интервала и 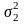, удовлетворяющие равенству

P[ 1-p. (3.6)

Для нормально распределенного Х известен закон распре­деления величины

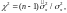(3.7)

который называют χ²-распределением Пирсона с f = n-1 сте­пенями свободы. После подстановки соотношения (3.7) в (3.6) при условии, что

P[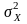 < ]=P[ > ]=p/2,

Получим

[χ² (p/2,f)≤ 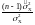≤χ²(1-p/2,f)]=1-p.

Величину χ²(1-p/2,f)=(n-1) 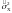/ находят по таблице 3.2 χ² распределения при вероятности 1-р/2 и числе степеней сво­боды f = n-1, а χ²(p/2,f)=(n-1) / определяют по таблице 3.2 при вероятности р/2 и числе степеней свободы f = n-1. Следовательно, доверительный интервал для дисперсии , соответствующий доверительной вероятности, есть

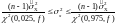. (3.8)

Величина находится аналогично .

3.3. Проверка статистических гипотез

Статистической гипотезой называют любое предположение о свойствах генеральной совокупности значений случайной величины. Выдвигаемые гипотезы можно подразделить на исходную или нуль-гипотезу Н₀ и конкурирующие (альтернативные) Н₁ и Н₂. Понятие статистической гипотезы означает предположе­ние о виде распределения случайной величины или о некото­ром параметре ее распределения. Проверка гипотезы заключа­ется в сопоставлении определенного статистического показа­теля (уровня значимости), вычисленного по данной выбор­ке, с уровнем значимости, найденным теоретически при ус­ловии, что проверяемая гипотеза верна.

Этот уровень соответ­ствует вероятности попадания значения статистического пока­зателя в так называемую критическую область, ограниченную критическими значениями определяемых параметров. Если значение параметра, вычис­ленное по данной выборке, попадает в критическую область, гипотеза отвергается. Если значение параметра не попа­дает в критическую область, данная выборка не дает основа­ний для того, чтобы проверяемая гипотеза была отвергнута.

При проверке гипотезы о том, что m_x=C, в качестве крите­рия используют величину

t=| -C|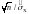 . (3.9)

Для m_y=C в (3.9) все величины Х надо заменить на величи­ны Y:

t=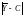 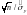, (3.9a)

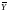Эта величина при условии, что гипотеза верна, имеет t-распределение Стьюдента с f=n-1 степенями свободы, где n — объем выборки при определении (или ), (или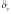 ). Если вычисленное по соотношению (3.9; 3.9a) значение t по абсолютной величине не превышает критического значения t_кр = t (p,f), найденного по таблице t-распределения при уровне значимости р и числе степеней свободы f=n-1 (т. е. | t | < t_кр), то гипотеза о том, что m_x=C (или m_y=C), принимается; в против­ном случае она отвергается.

Проверку гипотезы о равенстве двух математических ожи­даний m_x = m_у, вычисленных по двум выборкам случайных ве­личин Х и Y объемами n₁ и n₂, проводят по критерию

t=| - |/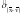 , (3.10)

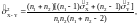
где

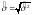
Критерий t имеет t-распределение Стьюдента с числом степеней свободы f=n₁+n₂-2 (табл. 3.1). Значения 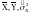и определяют по выборкам n₁ и n_2. Проверку гипо­тезы выполняют также, как в предыдущем случае, т. е. при | t | < t_кр гипотеза принимается, а при | t | > t_кр отвергается. Проверку гипотезы о равенстве дисперсий двух случайных ве­личин Х и Y, оценки которых и определены по двум выборкам объема n₁ и n_2, соответственно, проводят с использо­ванием критерия

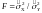, (3.11)

который имеет распределение Фишера со степенями сво­боды f₁=n₁-1 для числителя и f₂=n₂-1 для знаменателя. Полу­ченное по критерию (3.11) значение сравнивают с критическим значением F_кр= F(р, f₁, f₂), определяемым по таблице F-распределения (табл. 3.3) при уровне значимости р и степенях свободы f₁ для числителя и f₂ для знаменателя. Если F<F_кр, нет оснований для того, чтобы нулевая гипотеза была отвергнута; в противном случае принимаем, что на генеральной совокуп­ности .

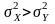При проверке гипотезы об отсутствии корреляции между двумя случайными величинами Х и Y используют отношение:

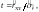(3.12)

где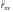 — оценка коэффициента корреляции, найденная по выборке объемом n; 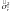=(1-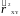 )/(n-2).

Величина t имеет t-распределение Стьюдента с f=n-2 сте­пенями свободы. Полученное по соотношению (3.12) значение t сравнивают с критическим t_кр= t(p,f), которое находят по таб­лице t-распределения (табл. 3.1) при уровне значимости р и степени свободы f. Если | t | < t_кр, нет оснований для того, что­бы гипотеза об отсутствии корреляции на генеральной сово­купности была отвергнута. В случае 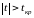принимаем, что между величинами Х и Y существует корреляция.

КОМПЬЮТЕРНЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ

Цель работы: изучение методов оценки параметров рас­пределения (математического ожидания, дисперсии, коэффи­циентов корреляции) и овладение методикой использования статистических критериев при проверке статистических гипо­тез.

Задание: Ознакомиться с методикой проведения экспери­мента по получению двух выборок случайных величин на ус­ловном химико-технологическом объекте. Выбрать свой вари­ант двух выборок из базы данных ПК (VarLD213. Документ MS WORD), провести статистическую оценку параметров распределения и проверить правильность гипотез. Затем уточ­нить результаты расчетов с помощью ПК по программам HYPOT. BAS или Проверка гипотез. Mcd — «Статистическая оценка параметров и проверка гипотез».

Порядок выполнения задания

1. Вычислить оценки математических ожиданий и по формуле (3.1), дисперсии и по формуле (3.2) и коэффи­циент корреляции по формуле (3.3).

2. Для заданной доверительной вероятности 1– р опреде­лить по таблице t-распределение Стьюдента (табл. 3.1), значе­ние (p,f) и найти доверительные интервалы для m_x и m_у по формуле (3.5).

3. По таблице χ²-распределения (табл. 3.2) опреде­лить значения χ²(p/2,f), χ²(1- p/2,f) и найти доверительные интервалы для

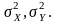
4. Для заданных значений С_x и С_у проверить гипотезы о ра­венстве m_x=C_x, m_у=C_у по формулам (3.9; 3.9a).

Рассчитать значение критерия t по формуле (3.10) и про­верить гипотезу о равенстве двух математических ожи­даний m_x = m_у, вычисленных по двум выборкам случайных ве­личин Х и Y объемами n₁ и n₂,

5. Рассчитать значение критерия F по формуле (3.11) и проверить гипотезу о равенстве дисперсий .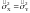

6. Рассчитать значение критерия t по формуле (3.12) и про­верить гипотезу об отсутствии корреляции между Х и Y.

Таблица 3.1