Дисперсионный анализ

В любом эксперименте средние значения наблюдаемых величин меняются в связи с изменением основных факторов (качественных и количественных), определяющих условия опыта, а также случайных факторов. Исследование влияния тех или иных факторов на изменчивость средних является за­дачей дисперсионного анализа.

Дисперсионный анализ — это первый статистический ме­тод отсеивания факторов в активном эксперименте. Активный эксперимент — это эксперимент, при анализе результатов ко­торого исследователь учитывает рекомендации математиче­ской теории планирования эксперимента. Он основан на пред­ставлении о том, что значимость фактора определяется его вкладом в дисперсию параметра оптимизации. Это обусловило широкое применение дисперсионного анализа при изучении точности различных методов измерений (особенно при анали­зе вещества). Он позволяет указывать на те факторы, которые вызвали ошибку, и отсеять незначимые, на улучшение кото­рых нецелесообразно затрачивать инженерные усилия. Дис­персионный анализ нужно использовать при оценке воспроиз­водимости результатов опытов, проводимых на пилотных ус­тановках. Воспроизводимость во времени служит характери­стикой качества изготовления установки; с учетом этой харак­теристики заказчик должен принимать установку от изготови­теля.

Дисперсионный анализ особенно эффективен при изуче­нии нескольких факторов.

При классическом методе исследования варьируют только один фактор, а остальные оставляют постоянными. При этом для каждого фактора проводится своя серия наблюдений, не используемая при изучении других факторов.

Дисперсионный анализ состоит в выделении и оценке от­дельных факторов, вызывающих изменчивость случайной ве­личины. Для этого производится разложение суммарной вы­борочной дисперсии на составляющие, обусловленные неза­висимыми факторами. Каждая из этих составляющих пред­ставляет собой оценку дисперсии генеральной совокупности. Чтобы решить, значимо ли влияние данного фактора, необхо­димо оценить значимость соответствующей выборочной дис­персии в сравнении с дисперсией воспроизводимости, обу­словленной случайными факторами. Проверка значимости оценок дисперсий проводится по критерию Фишера. Если рас­считанное значение критерия Фишера окажется больше таб­личного, то рассматриваемый фактор влияет на изменчивость средних значений. Если же рассчитанное значение критерия Фишера окажется меньше табличного, то нет основания счи­тать влияние рассматриваемого фактора значимым.

2.2. Однофакторный дисперсионный анализ

Рассмотрим действие единичного фактора А (количествен­ного или качественного), который принимает k различных значений (уровней фактора). На i-м уровне производится n_i наблюдений, результаты которых можно записать следующим образом:

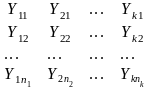
Будем полагать, что результаты любого наблюдения мож­но представить в виде модели

Y_ij = μ + d_i + ε_ij, (2.1)

где μ — суммарный эффект во всех опытах; d_i — эффект фак­тора А на i-м уровне (i = 1,2, …,k); ε_ij — ошибка измерения на i-м уровне.

Предположим, что наблюдения на фиксированном уровне фактора нормально распределены относительно среднего значе­ния μ+d_i с общей дисперсией σ². Общее число опытов равно N:

N = n₁+n₂+ … +n_k.

Проверяется нулевая гипотеза равенства средних значений на различных уровнях фактора А:

m₁ = m₂ = … = m_k = m. (2.2)

Наиболее простые расчеты получаются при равном числе опытов на каждом уровне фактора А:

n₁ =n₂ =…= n_k = n.

Общее число наблюдений N равно kn, где k — число серий опытов, а n — число параллельных опытов в серии.

Влияние фактора А является значимым, если

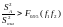, где f₁=k-1, f₂=k(n-1)=N-k. (2.3)

Обозначим через y_i среднее значение наблюдений на i-м уровне:`y_i =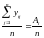 ,(2.4)

а общее среднее значение для всей выборки из N наблюдений

y_i =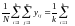 `y_i. (2.5)

Методика проведения эксперимента

Пусть необходимо провести эксперимент на условном хи­мико-технологическом объекте, в который поступают вещест­ва А и В, и в ходе химической реакции получается вещество D. Вход­ными параметрами объекта являются: СА — концентра­ция веще­ства А, СВ — концентрация вещества В. Каждому со­четанию СА и СВ соответствует определенное значение вы­ходной концентрации продукта CD, являющейся случайной величиной.

В результате проведения эксперимента должны быть по­лучены вероятностные характеристики для случайной величи­ны CD. Для этого необходимо:

1) задать значения СА, СВ, равные величинам нижних гра­ниц диапазона СА_mi,, CB_min;

2) провести 10 серий по 6 опытов в каждой по изменению значений СА при СВ=const;

3) провести аналогичную серию опытов по изменению СВ при СА=const.

4) варианты подобных выборок случайных величин вклю­чены в базу данных ПК [1].

Однофакторный дисперсионный анализ можно провести по следующему алгоритму [2]:

1) итоги по столбцам

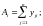(2.6)

2) сумма квадратов всех наблюдений

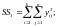(2.7)

3) сумма квадратов итогов по столбцам, деленная на число наблюдений в столбце

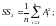(2.8)

4) квадрат общего итога, деленный на число всех наблю­дений (корректирующий член)

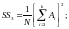(2.9)

5) сумма квадратов для столбца

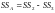. (2.10)

6) SS_общ — общая сумма квадратов, равная разнице между суммой квадратов всех наблюдений и корректи­рующим членом

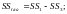(2.11)

7) SS_ост — остаточная сумма квадратов для оценки ошиб­ки эксперимента

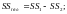(2.12)

8) дисперсия S_A²

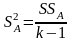; (2.13)

9) дисперсия S_ош²

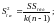(2.14)

Результаты расчета обычно представляются в виде табли­цы дисперсионного анализа (табл. 2.1).

Таблица 2.1