Решение задачи линейного программирования симплекс-методом с помощью Excel
Решение задачи легко выполнить с помощью надстройки Excel Поиск решения.
Введем исходные данные задачи в форму (рис. 1).
рис. 1.
2. Введем зависимости из математической модели (4) – (6).
2.1 Опишем целевую функцию с помощью функции СУММПРОЗВ:
курсор в F4;
обращаемся к Мастеру функций, категория Математические, функция СУММПРОИЗВ. На экране диалоговое окно СУММПРОИЗВ (рис. 2);
в массив 1 введем $B$3 : $E$3; в массив 2 – В4 : Е4;
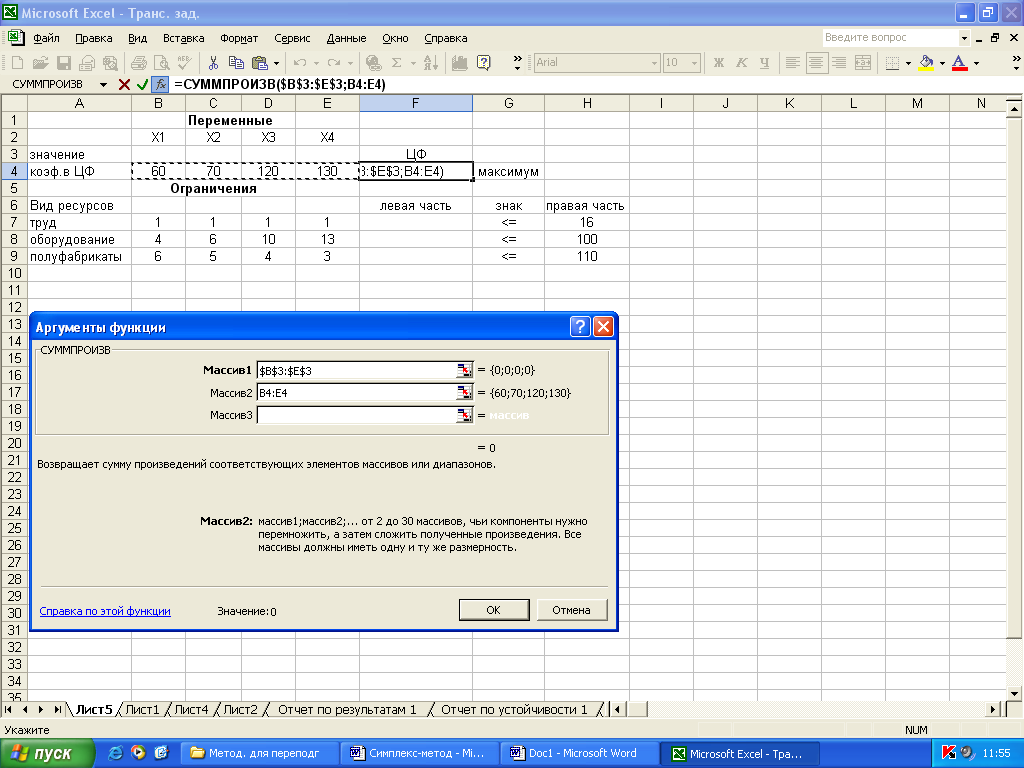
Рис. 2.
ОК; на экране: рис. 3, рис. 4 (в F4 введено значение целевой функции);
на рис. 3 показаны введенные зависимости для целевой функции и ограничений, а на рис. 4 эти зависимости – в режиме представления формул (Сервис, Параметры… в диалоговом окне Параметры – ярлычок Вид, выбрать Формулы).
Рис. 3.
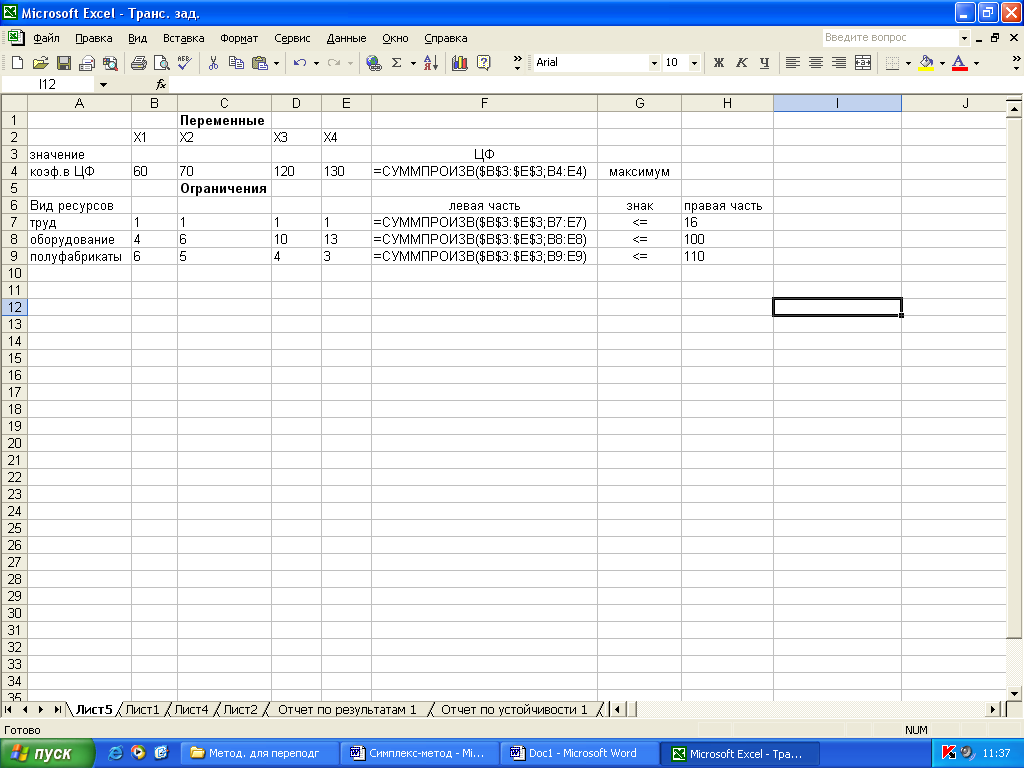
Рис. 4.
Введем зависимости для левых частей ограничений с помощью той же функции СУММПРОИЗВ:
курсор в F4;
копировать в буфер;
курсор в F7;
вставить из буфера. На экране: в F7 введена функция, как это показано на рис. 4;
скопировать F7 в F8:F9. На экране в F8:F9 введены функции (рис. 4).
3. Работа в диалоговом окне Поиск решения
3.1 Сервис, Поиск решения… на экране: диалоговое окно Поиск решения, представленное на рис. 5.
3.2. Введем целевую функцию:
курсор в окно Установить целевую ячейку;
введем адрес: F4;
введем направление оптимизации целевой функции: Максимальному значению.
3.3. Введем адреса искомых переменных:
курсов в поле Изменяя ячейки;
введем адреса: В3: Е3.
Рис. 5.
Добавить… На экране: диалоговое окно Добавление ограничения (рис. 6).
Рис. 6.
Введем ограничения: F7<=H7; F8<=H8; F9<=H9. После ввода последнего ограничения вместо Добавить… ввести ОК. На экране: диалоговое окно Поиск решения с введенными условиями (рис. 5).
Если при вводе значения возникает необходимость в изменении или удалении внесенных ограничений, то следует воспользоваться командами Изменить… Удалить…
Решение задачи.
После ввода параметров для решения ЗЛП следует открыть вкладку параметры и в открывшемся окне поставить флажки Линейная модель и Неотрицательные значения (рис. 7). Нажав кнопку ОК, вернемся в предыдущее окно, после чего следует нажать кнопку Выполнить. На экране появится сообщение о том, что решение найдено (рис. 8).
Полученное решение означает, что максимальную прибыль в 1320 ден. ед. предприятие может получить при выпуске 10 изделий первого вида и 6 изделий вида 3. При этом трудовые ресурсы и фонд времени работы оборудования будут использованы полностью, а полуфабрикатов будет использовано 84 кг.
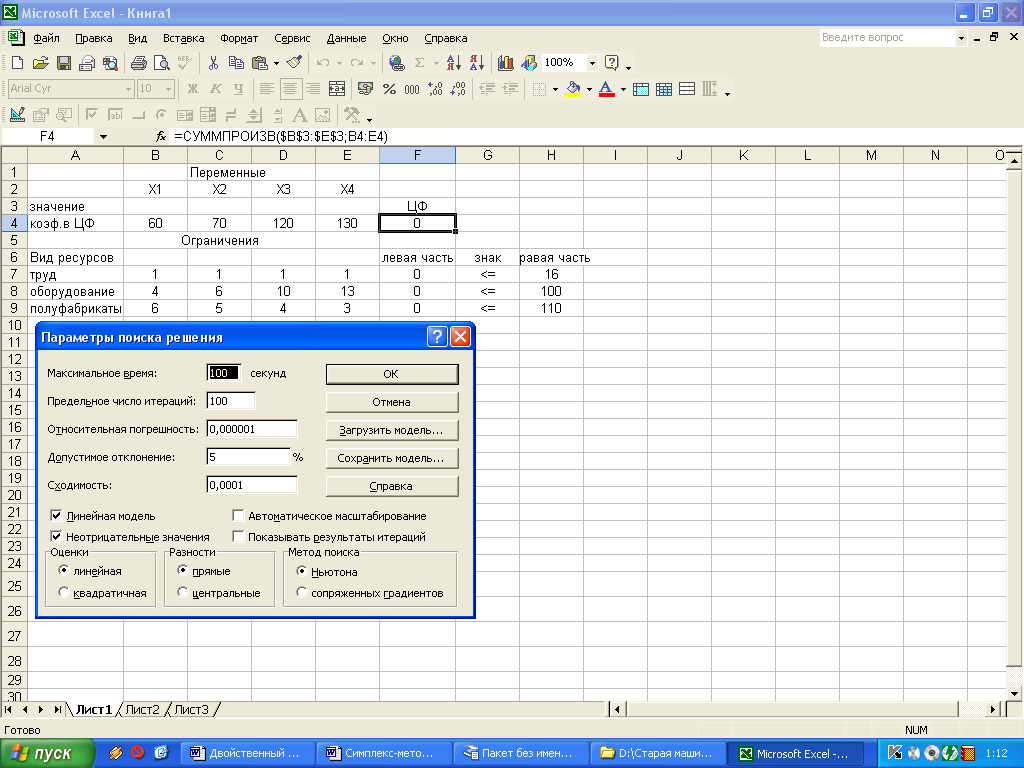
Рис. 7
Рис. 8
Excel позволяет представить результаты поиска решений в форме отчета трех типов:
Результаты. В отчет включаются исходные и конечные значения целевой и изменяемой ячеек, дополнительные сведения об ограничениях.
Устойчивость. Отчет, содержащий сведения о чувствительности решения к малым изменениям в изменяемых ячейках или в формулах ограничений.
Пределы. Помимо исходных и конечных значений изменяемых и целевой ячеек, в отчет включаются верхние и нижние границы значений, которые могут принимать влияющие ячейки при соблюдении ограничений.
1 При формировании оптимального плана не всегда оказывается достаточным лучших ресурсов, поэтому иногда приходится принимать во внимание и не самые выгодные способы формирования результата, а какой из них войдет в оптимальный план – зависит от того, насколько он там нужен.