3. Переход к новому опорному плану

Поскольку проверяемое решение не является оптимальным, найдем другое опорное решение, «улучшающее» значение целевой функции. Это возможно только в том случае, если возрастание какой-либо свободной (нулевой) переменной ведет к улучшению значения целевой функции. Но для того, чтобы свободная переменная стала положительной (перешла в число базисных переменных), надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в разряд свободных. Это необходимо, чтобы новое решение содержало в точности m базисных переменных.

Таким образом, переход к новому опорному плану осуществляется путем замены базисных переменных. При этом выбранная для ввода в число базисных свободная переменная называется вводимой, а удаляемая в разряд свободных базисная переменная – выводимой.

1. Выбор вводимой в число базисных переменной: вводимая в число базисных переменная определяется максимальной по абсолютной величине отрицательной оценкой при решении задачи на максимум целевой функции и наибольшей положительной оценкой – при решении задачи на минимум. Соответствующий столбец коэффициентов в симплекс-таблице будем называть ключевым.

В целевой строке таблицы 3 имеются отрицательные оценки. Максимальная по модулю среди них – ∆₄ = -130, поэтому, следуя правилу в качестве вводимой переменной надо взять х₄, но мы от этого правила несколько отклонимся (объяснение этому последует позже) и выберем х₃. Соответствующий ключевой столбец в табл. 4 выделен цветом.

2. Выбор выводимой из числа базисных (в разряд свободных) переменной осуществляется следующим образом: выводимая из числа базисных переменная независимо от направленности оптимизации определяется по минимальному симплекс-отношению. Симплекс-отношение представляет собой отношение элементов итогового столбца симплекс-таблицы к соответствующим положительным элементам ключевого столбца. Соответствующая выводимой переменной строка в симплекс-таблице называется ключевой.

Для записи симплекс-отношений в таблице имеется специальный столбец (α). Минимальное из симплекс-отношений (табл. 4) определяет ключевую строку (она выделена цветом) и выводимую из числа базисных переменную – это х₆.

Итак, замена в базисе осуществлена: в разряд свободных выводится х₆ и ее место занимает х₃, что находит отражение в симплекс-таблице 5 (ключевой столбец соответствует переменной х₃, а ключевая строка – переменной х₆).

Элемент, находящийся на пересечении ключевой строки и ключевого столбца (число 10), называется ключевым элементом и будет использован для пересчета элементов симплекс-таблицы.

Таблица 4.

Cj	Базис		B	60		70		120		130		0		0		0	α		β
				А1		А2		А3		А4		А5		А6		А7
0	X5		16	1		1		1		1		1		0		0	16		0,1
0	X6		100	4		6		10		13		0		1		0	10		1
0	X7		110	6		5		4		3		0		0		1	27,5		0,4
∆j=zj - cj		0		-60	-70		-120		-130		0		0		0			-12

Следующий шаг на этапе перехода к новому опорному плану – пересчет всех элементов таблицы, который выполняется по следующему правилу, состоящему из двух частей.

1). Элементы ключевой строки делятся на ключевой элемент. Полученные таким образом величины помещают в новую таблицу. Так в табл. 6 элементы строки х₃ равны:

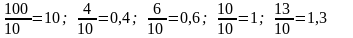и т.д.

2). Все остальные элементы, включая целевую строку, преобразовываются по правилу «треугольника»:

а) в столбец β записываются отношения элементов ключевого столбца к ключевому элементу: 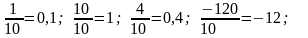(см. табл. 4);

б) пересчет элементов выполняется в соответствии со схемой

b

а^новое = а^старое – b ∙ с

c

a

где b – элемент, находящийся на пересечении столбца, содержащего пересчитываемое число, и ключевой строки; с – элемент, находящийся на пересечении строки, содержащей пересчитываемое число, и столбца β.

Так, элементы первой строки табл. 5 получены из соответствующих элементов табл. 4 следующим образом:

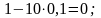
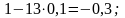
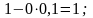
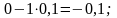
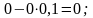
третьей строки:

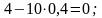
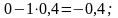
целевой строки:

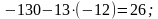
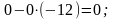
Результаты вычислений представлены в табл. 5.

Таблица 5.

Ci	Базис	B	60	70	120	130	0	0	0	α	β
			А1	А2	А3	А4	А5	А6	А7
0	X5	6	0,6	0,4	0	-0,3	1	-0,1	0	10	1
120	X3	10	0,4	0,6	1	1,3	0	0,1	0	25	0,666667
0	X7	70	4,4	2,6	0	-2,2	0	-0,4	1	15,91	7,333333
∆j=zj - cj		1200	-12	2	0	26	0	12	0		-20

Поскольку среди оценок таблицы 5 еще имеется отрицательная ∆₁ = -12, то делаем вывод о том, что новое решение не является оптимальным. Переменная х₁ теперь вводимая, х₅ – выводимая.

Выполнив пересчет, приходим к таблице 6, которая, как видим, содержит оптимальное решение задачи.

Таблица 6.

Ci	Базис	B	60	70	120	130	0	0	0
			А1	А2	А3	А4	А5	А6	А7
60	X1	10	1	0,6667	0	-0,5	1,667	-0,167	0
120	X3	6	0	0,3333	1	1,5	-0,667	0,1667	0
0	X7	26	0	-0,333	0	0	-7,333	0,3333	1
∆j=zj - cj		1320	0	10	0	20	20	10	0

Или Таблица 6. – Оптимальный план выпуска продукции

Ci	Базис	B	60	70	120	130	0	0	0
			х1	х2	х3	х4	х5	х6	х7
60	X1	10	1		0				0
120	X3	6	0		1				0
0	X7	26	0		0	0			1
∆j=zj - cj		1320	0	10	0	20	20	10	0

Оптимальный план предусматривает выпуск десяти изделий первого вида (х₁ = 10) и шести изделий третьего вида (х₃ = 6); среди базисных отсутствуют переменные х₂ и х₄ , следовательно, выпуск продукции второго и четвертого видов не планируется. Базисная переменная х₇ = 26 означает, что ресурс третьего вида (полуфабрикаты) недоиспользован, резерв этого ресурса равен 26 кг. Максимальная прибыль при этом составляет 1320 грн.