Алгоритм графического решения задач линейного программирования
1. Записывают уравнения граничных прямых
ai1x1 + aix2 = bi (i = 1,2,…,m)
строят их на плоскости x10x2 .
2. Определяют полуплоскости, которые соответствуют каждому ограничению-неравенству. Для этого берут произвольную точку, которая не находится на прямой, и её координаты подставляют в ограничение-неравенство. Если неравенство в выбранной точке выполняется, то искомая полуплоскость будет та, которая содержит выбранную точку, если нет, то неравенство определяет полуплоскость, в которой не лежит выбранная точка.
3. Выделяют ОДP. Если имеется условие неотрицательности переменных, то ОДP расположена в первой четверти. x2 ≥ 0 определяет верхнюю полуплоскость, x1 ≥ 0 – правую полуплоскость.
4. Строят вектор с = (с1; с2 ) – направление наибольшего возрастания функции F .
5. Строят прямую перпендикулярную вектору с .
6. Перемещают эту прямую в направлении вектора с , если задача на max, и в противоположном направлении, если задача на min, пока она станет опорной. Если прямая не может стать опорной, то F → −∞ или F → +∞.
7. Вычисляют координаты оптимальной точки и оптимальное значение функции F.
В зависимости от вида ОДР и положения линий уровня целевой функции возможны следующие случаи:
ОДР, изображенная на рис. 3 и 4, соответствует одной и той же системе ограничений
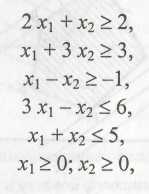
но функции, которые максимизируются, отличаются друг от друга:
в первом случае: F = х1 + 2 х2,
во втором: F = x1 + x2.
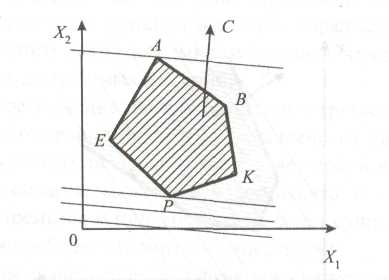
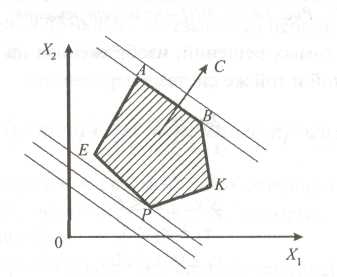
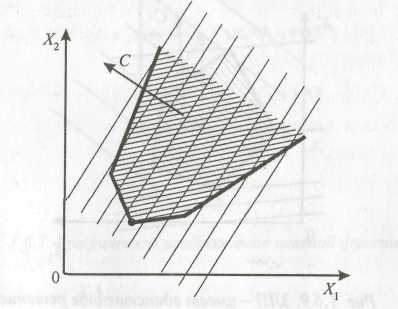
Рис. 6
примеры, представленные на рис. 3 – 6 показывают, что:
оптимальное значение целевой функции в первом примере, графическое изображение которого представлено на рис. 3, достигается в одной единственной точке;
оптимальное значение во втором примере, графическое изображение которого представлено на рис. 4, достигается в двух вершинах выпуклого многоугольника и, следовательно, в любой точке отрезка АВ. Говорят, что в этом случае задача имеет альтернативный оптимум, т.е. имеет множество оптимальных решений. Таким образом, если оптимальное значение функции F достигается в двух вершинах, то оптимального значения целевая функция достигает в любой точке, соединяющей эти две вершины. Произошло это потому, что линии уровня целевой функции оказались параллельны одной из сторон замкнутого выпуклого многоугольника, представляющего собой область допустимых решений;
оптимальное значение целевой функции в третьем примере, графическое изображение которого представлено на рис. 5, где область допустимых решений представляет собой выпуклую неограниченную область, может быть достигнуто в (.)В, если целевая функция стремится к минимуму, и не будет существовать, если целевая функция будет стремиться к максимуму;
оптимальное значение целевой функции в четвертом примере, графическое изображение которого представлено на рис. 6, где область допустимых решений представляет собой выпуклую неограниченную область, а целевая функция F оказывается неограниченной ни сверху, ни снизу, - не существует.
В теории линейного программирования доказан ряд теорем, из которых вытекают свойства решений задачи линейного программирования, которые хорошо иллюстрированы рассмотренной графической интерпретацией.
1. Множество всех допустимых решений системы ограничений ЗЛП является выпуклым (если оно не пусто) с конечным числом угловых точек.
2. Если ЗЛП имеет оптимальное решение, то целевая функция принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если целевая функция принимает максимальное (минимальное) значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.
3. Необходимым и достаточным условием существования оптимального решения ЗЛП является ограниченность целевой функции в ОДР.
4. Каждому допустимому базисному (опорному) решению ЗЛП соответствует угловая точка многогранника решений, и, наоборот, каждой угловой точку многогранника решений соответствует допустимое базисное решение.
Итак, оптимум целевой функции ЗЛП следует искать среди конечного числа ее допустимых базисных (опорных) решений.