
- •3.2 Различные формы задач линейного программирования
- •Графический метод и свойства решений
- •Алгоритм графического решения задач линейного программирования
- •Симплекс-метод
- •Определение начального опорного решения (плана)
- •Проверка полученного опорного решения на оптимальность
- •Переход к новому опорному плану
- •Решение задачи линейного программирования симплекс-методом с помощью Excel
Понятие модели
Для принятия эффективных решений в планировании и управлении производством необходимо экономическую сущность исследуемого экономического объекта формализовать экономико-математической моделью.
модель – это условный образ объекта (в качестве которого могут выступать системы или понятия), формирующий представление о нем в некоторой форме, отличной от реального существования данного объекта.
Математическая модель экономического объекта – это отображение основных закономерностей в виде совокупности уравнений, неравенств, логических отношений.
Для построения экономико-математической модели используется следующий алгоритм:
Формируются предмет и цели исследования.
В рассматриваемой экономической системе выделяются определенные элементы, соответствующие данной цели исследования, и наиболее важные характеристики этих элементов.
Словесно описываются взаимосвязи между элементами модели.
Вводятся символические обозначения для учитываемых характеристик экономического объекта и устанавливаются, насколько возможно, взаимосвязи между ними. Тем самым формируется математическая модель.
По данной модели проводятся расчеты и анализ полученного решения.
Оптимизационные модели
Отличительными признаками оптимизационных моделей являются:
наличие одного или нескольких критериев оптимальности (критерий оптимальности - это признак, по которому множество или одно решение задачи признается наилучшим); наиболее типичными критериями в экономических оптимизационных задачах являются: максимум дохода или прибыли, минимум издержек, минимальное время для выполнения задания и другие;
система ограничений, которая формируется, исходя из содержательной постановки задачи, и представляет собой систему уравнений или неравенств.
Оптимизационная задача в общем виде:
Найти
значения переменных
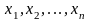 ,
которые удовлетворяют системе неравенств
(уравнений)
,
которые удовлетворяют системе неравенств
(уравнений)
gi ( ) ≤ bi, i = 1,2,…,m (1)
и обращают в максимум (или минимум) целевую функцию
F = f ( ) → max (min) (2)
(Условия неотрицательности переменных, если они есть, входят в ограничения (1)).
для решения задачи (1) – (2) применяются методы математического программирования.
Если целевая функция (2) и ограничения (1) представлены линейными функциями, то такая задача является задачей линейного программирования.
Если, исходя из содержательного смысла, ее решение должно быть выражено целыми числами, то это задача целочисленного линейного программирования.
Если целевая функция (2) и (или) ограничения (1) задаются нелинейными функциями, то имеем задачу нелинейного программирования. В частности, если указанные функции обладают свойствами выпуклости, то полученная задача является задачей выпуклого программирования.
Если функции f и (или) gi в выражениях (2) и (1) зависят от параметров, то получаем задачу параметрического программирования, если эти функции носят случайный характер, – задачу стохастического программирования.
Если речь идет о процессе поэтапного принятия решений, разворачивающегося во времени, то имеем задачу динамического программирования.
В задаче математического программирования функцию F= f ( ) называют целевой функцией; систему неравенств (1) – ограничениями задачи.
Из перечисленных методов математического программирования наиболее распространенным и разработанным является линейное программирование.
1 Примеры моделей линейного программирования
Задача об оптимальном использовании ресурсов
Для изготовления двух видов продукции П1 и П2 используются четыре вида ресурсов: Р1, Р2, Р3, Р4. Имеющиеся запасы ресурсов различных видов, а также затраты на изготовление единицы каждого из видов продукции приведены в таблице 1.
Таблица 1.
Вид ресурса |
Расход ресурса на единицу продукции вида |
Запас ресурса |
|
П1 |
П2 |
||
Р1 |
1 |
3 |
18 |
Р2 |
2 |
1 |
16 |
Р3 |
0 |
1 |
5 |
Р4 |
3 |
0 |
21 |
Выручка, получаемая предприятием от продажи единиц продукции П1 и П2 составляет соответственно 2 грн. и 3 грн.
Необходимо составить такой план производства продукции, при котором выручка предприятия от ее реализации будет наибольшей.
Составим экономико-математическую модель задачи.
Обозначим через х1 – число единиц продукции первого вида, которое запланировано к производству; х2 – число единиц продукции второго вида, которое запланировано к производству.
На изготовление продукции П1 и П2 в количестве соответственно х1 и х2 единиц потребуется:
1х1 + 3х2 единиц ресурса Р1;
2х1 + 1х2 единиц ресурса Р2;
1х2 единиц ресурса Р3;
3х1 единиц ресурса Р4.
Так как потребление ресурсов не должно превышать их запаса, то связь между потреблением ресурсов и их запасами выразится системой ограничений:
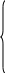 1х1
+ 3х2
18;
1х1
+ 3х2
18;
2х1 + 1х2 16; (3)
1х2 5;
3х1 21.
На переменные накладывается условие неотрицательности, вполне соответствующее смыслу задачи (количество выпускаемой продукции не может быть отрицательным):
х1 0, х2 0. (4)
Выручка от реализации продукции П1 составит 2х1, а от реализации продукции П2 – 3х2, таким образом, суммарная выручка от реализации обоих видов продукции составит:
F = 2х1 + 3х2. (5)
Выражение (5) определяет критерий оптимальности задачи, формализованный в виде так называемой «целевой функции».
Требуется найти такой план выпуска продукции Х = (х1, х2), который удовлетворял бы ограничениям (3) и (4) и при котором целевая функция (5) принимала бы максимальное значение:
F = 2х1 + 3х2 max
 1х1
+ 3х2
18;
1х1
+ 3х2
18;
2х1 + 1х2 16;
1х2 5;
3х1 21;
х1 0, х2 0.
Эту задачу легко обобщить на n видов продукции и m видов ресурсов. Обозначим через:
xj – число единиц j- го вида продукции (j = 1,2,…,n), запланированной к производству;
bi – имеющееся в распоряжении количество (запас) i- го ресурса (i = 1,2,…,m);
aij – число единиц ресурса i, затрачиваемого на изготовление единицы продукции j - го вида (aij часто называют технологическими коэффициентами);
cj – выручка от реализации единицы продукции j- го вида (или цена единицы продукции j- го вида) (j = 1,2,…,n).
Тогда экономико-математическая модель задачи об использовании ресурсов в общей постановке примет вид:
найти такой план выпуска продукции Х = (х1, х2,…, хn), который удовлетворял бы системе ограничений:
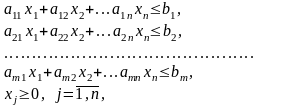
и при этом целевая функция достигала бы своего максимального значения:
 .
.
Задача о раскрое материалов.
Для изготовления брусьев длиной 1,5 м, 3 м и 5 м в соотношении 2 1 3 на распил поступают 200 бревен длиной 6 м. Найти план распила, обеспечивающий максимальное число комплектов.
Чтобы сформулировать экономико-математическую модель данной задачи, необходимо вначале определить все возможные варианты распила бревен, указав соответствующее число получаемых при этом брусьев (табл. 2).
Таблица 2.
Длина брусьев |
Число получаемых брусьев
|
Способ распила i |
|||
1 |
2 |
3 |
4 |
||
1,5 |
4 |
2 |
- |
- |
|
3 |
- |
1 |
2 |
- |
|
5 |
- |
- |
- |
1 |
|
Величина отходов, м |
0 |
0 |
0 |
1 |
|
Варианты, представленные в табл. 2, означают следующее:
из 6-метрового бревна можно получить 4 бруса длиной 1,5 м, при этом отходов не будет;
в 6 метров укладывается 2 бруска по 1,5 м (итого 3 метра) и один 3-метровый брусок, величина отходов, как и в первом варианте, равна нулю;
два бруска длиной по 3 метра, опять безотходный вариант;
один 5-метровый брусок укладывается в 6 метров длины бревна, отправляя один метр в отходы.
Видим, что четвертый вариант раскроя хуже других (с точки зрения величины отходов), но, поскольку при построении модели необходимо принять во внимание все возможные способы, этот вариант не исключаем1.
Обозначим через хj – число бревен, распиленных j-м способом (j = 1,2,3,4); у – число комплектов брусьев.
Первый способ предполагает, что из одного бревна длиной 6 м будет получено брусьев первого вида (длиной 1,5 м) 4 штуки, отходы при этом равны нулю. Второй способ раскроя позволит получить 2 бруса длиной 1,5 м и один длиной 3 м и т.д.
Построим математическую модель задачи.
Так как хj – число бревен, распиленных j-м способом, то общее количество распиленных бревен будет равно: х1 + х2 + х3 + х4 . Поскольку нельзя распилить бревен больше, чем имеется, то ограничение по количеству исходного материала имеет вид:
х1 + х2 + х3 + х4 200.
Учитывая, что по первому способу будет распилено х1 бревен, получим 4х1 брусьев первого вида. Второй способ раскроя даст 2х2 этих брусьев, третий и четвертый способы не предусматривают получение брусьев длиной 1,5 м. Поэтому общее количество данной продукции составит 4х1 + 2х2 штук. В каждый комплект входит 2 таких бруса, а число комплектов равно у, следовательно ограничение по количеству данного вида брусьев (включая условие комплектности) представляется в виде:
4х1 + 2х2 = 2у.
Аналогично записываются ограничения по количеству продукции второго, третьего и четвертого видов.
Оптимизационная экономико-математическая модель примет вид:

х1 + х2 + х3 + х4 200;
4х1 + 2х2 = 2у;
1х2 + 2х3 = у;
1х4 = 3у.

задачу о раскрое легко обобщить на случай m видов раскраиваемых материалов.
Пусть каждая единица i - го материала (i = 1,2,…,m) может быть раскроена n различными способами, причем использование j – го способа (j = 1,2,…,n) дает ajik единиц k - го изделия (k = 1,2,…,K), запас i - го материала равен bi единиц, а число изделий k – го вида, входящих в комплект, равняется сk.
Обозначим хij – число единиц i - го материала, раскраиваемого j – м способом, у – число комплектов изделий.
экономико-математическая модель задачи о раскрое в общей постановке примет вид:


 .
.
Рассмотрев частные постановки задачи линейного программирования, обобщим полученные представления.
3.2 Различные формы задач линейного программирования
В
самом общем виде задача линейного
программирования (ЗЛП) формулируется
следующим образом: найти вектор
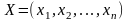 ,
доставляющий
экстремум (максимум или минимум) линейной
целевой функции
,
доставляющий
экстремум (максимум или минимум) линейной
целевой функции
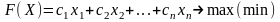 (6)
(6)
и удовлетворяющий ограничениям (условиям):
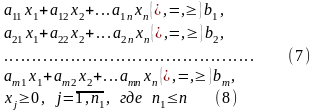
в зависимости от наличия ограничений разного типа различают следующие три основные формы ЗЛП.
Задача (6) – (8) представляет общую задачу линейного программирования; она характеризуется тем, что включает как ограничения-равенства, так и ограничения-неравенства, кроме того, не на все переменные накладывается условие неотрицательности.
ЗЛП записана в канонической (стандартной) форме, если все ограничения представлены в виде равенств и на все переменные накладывается условие неотрицательности. Таковой является модель (9) – (11).
 (9)
(9)
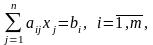 (10)
(10)
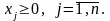 (11)
(11)
Симметричная форма задачи линейного программирования, которая важна в виду большого числа прикладных моделей, содержит только ограничения-неравенства и часто используется в одном из следующих видов:
1.
 2.
2.


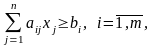
Переход от одной формы к другой осуществляется на основе простых преобразований. Так, для перехода от ограничения-неравенства к равенству в левую часть неравенства достаточно ввести дополнительную неотрицательную переменную с коэффициентом (+1 ), если неравенство имеет вид « ≤ », и с коэффициентом ( -1 ), – если неравенство типа « ≥ ».
От ограничений-равенств можно перейти к неравенствам, заменяя каждое уравнение,

двумя неравенствами противоположного типа:
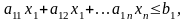

Общая задача линейного программирования (6) – (8) записана в «развернутом виде». Запись же канонической и симметричной форм ЗЛП более сжата, здесь использованы знаки суммирования.
Вектор , удовлетворяющий всем ограничениям задачи, называется допустимым решением, или допустимым планом. Множество всех допустимых планов называется допустимым множеством, или областью допустимых решений задачи. Допустимое решение, обращающее в максимум или минимум целевую функцию, называется оптимальным решением, или оптимальным планом.
Допустимый план называется опорным, если положительным компонентам вектора-решения соответствует линейно независимая система вектор-столбцов матрицы условий задачи (А).
Следует заметить, что поскольку задачи математического программирования предполагают свободу выбора решений, то случай, когда число ограничений m равно числу переменных n, не представляет интереса, так как при m = n, если система уравнений совместна, то задача имеет единственное решение, которое и является оптимальным. Поэтому далее будем считать, что m < n.
Из того, что векторы коэффициентов Aj матрицы А являются m-мерными, следует, что опорное решение ЗЛП не может иметь больше, чем m положительных компонент.
Опорное решение называется невырожденным, если оно включает ровно m положительных компонент, и вырожденным – если число положительных компонент меньше m.
Базисом опорного решения называется система из m линейно независимых векторов, включающая все столбцы коэффициентов Aj матрицы А, соответствующие положительным компонентам этого опорного решения.
Компоненты опорного плана, соответствующие векторам его базиса, называются базисными, а остальные – свободными.
