Задачи для самостоятельной работы

1. Отдел технического контроля обнаружил 5 бракованных деталей из 100 проверенных. Определить относительную частоту появления стандартных деталей.

2. Из родившихся в течение некоторого периода времени 11000 детей зарегистрировано 6452 мальчика. Определить частоту рождения детей того и другого пола.

3. Произведя 100 выстрелов, стрелок попал в цель 76 раз. Определить относительную частоту промаха этого стрелка.

4. На 10000 человек населения в 1960 году приходилось 62 студента, а в 2009 году – 432. Определить, как изменилась относительная частота студентов за этот период.

5. В некоторый период времени относительная частота солнечных дней составила 0,6 . Сколько дней было пасмурных, если солнечных дней было 42?

6. Относительная частота попадания у данного стрелка оказалась равной 0,9. Сколько он произвел выстрелов, если промахнулся 9 раз?

7. В обувном магазине в течение месяца проводилось обследование частоты спроса женской обуви по размерам. Результаты обследования представлены в таблице. Определить относительную частоту спроса по размерам. Чему равна сумма относительных частот?

   Размер обуви	35	36	37	38	39	40
   Частота спроса

8. В ящике 20 шаров: из них 5 белых, 4 черных, 5 красных, 6 зеленых. Определить вероятность того, что извлеченный наугад шар будет цветным.

9. Определить вероятность того, что при бросании игральной кости выпадает грань с четным числом очков.

10. В партии из 100 деталей 4 бракованных. Определить вероятность того, что наугад взятая деталь окажется: а) годной, в) бракованной?

11. В ящике 100 деталей, из которых 7 бракованных. Число 0,07 – это вероятность или относительная частота извлечения бракованной детали из ящика?

12. Контролер проверяет детали, сходящие с конвейера. При проверке 100 деталей оказалось 7 деталей бракованных. Число 0,07 – это вероятность или относительная частота извлечения бракованной детали из ящика?

13. В лотерее 100 билетов: среди них один выигрыш в 10000 рублей, три выигрыша по 5000 рублей, шесть выигрышей по 2500 рублей и 10 выигрышей по 300 рублей. Некто покупает один билет. Определить вероятность событий: 1) выигрыш не менее 2500 рублей; 2)выигрыш не более 2500 рублей.

14. Через остановку проходят автобусы следующих маршрутов: № 2,5,6,8,20. Пассажира устраивают маршруты №5 и №8. Определить вероятность того, что первый подошедший к остановке автобус будет нужного ему маршрута, если известно, что второго маршрута 8 машин, пятого – 15, шестого – 12, восьмого – 10, двадцатого – 5.

15. В круг радиуса 5 см вписан правильный треугольник. Определить вероятность того, что точка, брошенная на круг, окажется внутри треугольника.

16. В квадрат со стороной 2 см вписан круг. Определить вероятность того, что точка, брошенная на квадрат, окажется внутри круга.

17. На отрезок длины 1 бросают наугад 2 точки. Они разбивают отрезок на 3 части. Какова вероятность того, что из полученных 3 отрезков можно сложить треугольник?

18. Из полной колоды карт ( 52 карты) вынимаются наугад 3 карты (без возврата). Вычислить вероятность того, что среди вынутых карт будет: а) точно один туз; в) хотя бы один туз.

19. Какова вероятность появления слова ДВА, если наугад выбираются 3 карточки из пяти с буквами А, Б, В, Г, Д и располагаются в ряд в порядке появления?

20. Из урны с шарами, на которых написаны буквы, составляющие слово ФИЛОСОФИЯ, выбирают наугад последовательно 4 шара и укладывают один  за другим в порядке их появления. Какова вероятность того, что при этом сложится слово СОЛО?

21. Брошены 2 игральные кости. Найти вероятность следующего события А = {сумма выпавших очков равна 8}.

22. Какова вероятность появления слова ТРИ, если наугад выбираются 3 карточки из шести с буквами А, И, Т, О, М, Р и располагаются в ряд в порядке появления?

23. Из 30 экзаменационных билетов студент может ответить на 24. Какова вероятность его успешного ответа на экзамене на билет при однократном извлечении билета?

24. Из карточек, из которых составлено слово ДИСПЛЕЙ, случайным образом выбраны 3 и выложены в ряд. Какова вероятность, что они образовали слово ЛЕС?

25. Студент из 30 вопросов к экзамену хорошо усвоил 24. Какова вероятность, что он знает оба из доставшихся ему вопросов?

СЛОВАРЬ ТЕРМИНОВ

Probability	Вероятность
Event	Событие
Elementary event	Элементарное событие
Compound event	Сложное (составное) событие
Complement event	Противоположное событие
Venn diagram	Диаграммы Венна
Mutually exclusive events	Несовместные события
Exhaustive events	Совместные события
Total probability	Полная вероятность
Conditional probability	Условная вероятность
Independent events	Независимые события
Tree diagram	Древовидная диаграмма
Bayes’ theorem	Теорема Байеса
“At least” problems	Задачи «по крайней мере»

Probability of an elementary events

In the presumed knowledge section we considered the idea that when we look at an experimental situation we find answers that indicate that a theoretical application is appropriate. This theoretical approach is called probability and is what we will explore in this chapter. Consider a number of equally likely outcomes of an event. What is the probability of one specific outcome of that event? For example, if we have a cubical die what is the probability of throwing a six?

Since there are six equally likely outcomes and only one of them is throwing a six, then the probability of throwing a six is 1 in 6. We would normally write this as a fraction or as a decimal or a percentage. Since probability is a theoretical concept, it does not mean that if we throw a die six times we will definitely get a six on one of the throws.

However, as the number of trials increases, the number of sixes becomes closer to 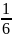of the total.

Generally, if the probability space S consists of a finite number of equally likely outcomes, then the probability of an event E, written P(E) is defined as:

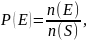where n(E) is the number of occurrences of the event E and n(S) is the total number of possible outcomes.

Hence in a room of fifteen people, if seven of them have blue eyes, then the probability that a person picked at random will have blue eyes is

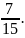
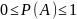
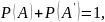where P(A’) is the probability that the event A does not occur. A’ is known as the complement of A.

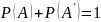where P(A’) is the probability that the event A does not occur.

EXAMPLES

Example 1

Two coins are tossed simultaneously. Find the probability of getting at least one head.

Solution

i) Event E: ‘getting at least one head’

ii) Outcomes favorable to the event: {(H,H) (H,T), (T,H)}

iii) Number of outcomes favorable to the event: 3

iv) All possible outcomes of the experiment (sample space): {(H,H) (H,T), (T,H), (T,T)}

v) Number of all possible outcomes of the experiment: 4

vi) Probability of ‘getting at least one head’=3/4

Example 2

A bag consists of 5 red balls, 3 white balls and 2 green balls. A ball is drawn from the bag at random. What is the probability of drawing a white ball?

Solution

i) Event E: ‘drawing a white ball’

ii) Outcomes favorable to the event: {x l x is a white ball}

iii) Number of outcomes favorable to the event: 3

iv) All possible outcomes of the experiment (sample space): {x l x is a ball in the bag}

v) Number of all possible outcomes of the experiment: 10

vi) Probability of ‘drawing a white ball’=3/10

EXERCISES

1. An unbiased tetrahedral die is thrown. What is the probability of throwing

   1. a three

   2. an even number

   3. a prime number?

2. A spinner has the numbers 1 to 10 written on it. When spun, it is equally likely to stop on any of the ten numbers. What is the probability that it will stop on

   1. a three

   2. an odd number

   3. a multiple of 3

   4. a prime number?

3. A bag contains 5 black balls, 6 white balls, 7 pink balls and 2 blue balls. What is the probability that a ball drawn randomly from the bag will

   1. be a black ball

   2. be either a white or a pink ball

   3. not be a blue ball

   4. be either a black, white or blue ball

   5. be a red ball?

4. A die is thrown once. What is the probability of getting 6 on the top?

5. A card is drawn from a well shuffled pack of 52 cards. What is the probability of getting a face card?

6. In question number 5, what is the probability of not getting a hearts?

7. Two dice are thrown once. What is the probability that sum of the two numbers appearing on the top of the dice is more than 10?

8. A carton consists of 200 electric bulbs. Out of which 20 bulbs are fused. One bulb is taken out of the carton at random. What is the probability that the bulb is not fused?