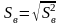Числовые характеристики дискретной случайной величины.

Определение: Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности: М(Х)=∑ x_iр_i= x₁р₁ + x₂р₂+…+ x_nр_n

Математическое ожидание служит характеристикой среднего значения случайной величины.

Свойства математического ожидания:

1)M(C)=C, где С-постоянная величина;

2)М(С•Х)=С•М(Х),

3)М(Х±Y)=М(Х) ±M(Y);

4)M(X•Y)=M(X) •M(Y), где X,Y- независимые случайные величины;

5)M(X±C)=M(X)±C, где С-постоянная величина;

Определение: Дисперсией D(X) случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X)=M(X-M(X))²

Свойства дисперсии:

1)D(C)=0, где С-постоянная величина;

2)D(X)>0, где Х- случайная величина;

3)D(C•X)=C²•D(X), где С-постоянная величина;

4)D(X+Y)=D(X)+D(Y), где X,Y- независимые случайные величины;

Для вычисления дисперсии часто бывает удобно пользоваться формулой:

D(X)=M(X²)-(M(X))²,где М(Х)=∑ x_i²р_i= x₁²р₁ + x₂²р₂+…+ x_n²р_n

Определение: Средним квадратическим отклонением σ(Х) случайной величины Х называется квадратный корень из дисперсии:

Задача 2. Дискретная случайная величина Х задана законом распределения:

х	-1	0	1	2	3
р	0,1	Р2	0,3	0,2	0,3

Найти Р₂, функцию распределения F(x) и построить ее график, а также M(X),D(X), σ(Х).

Решение: Так как сумма вероятностей возможных значений случайной величины Х равна 1, то

Р₂=1- (0,1+0,3+0,2+0,3)=0,1

Найдем функцию распределения F(х)=P(X<x).

Геометрически это равенство можно истолковать так: F(х) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.

Если х≤-1, то F(х)=0, т.к. на (-∞; х) нет ни одного значения данной случайной величины;

если -1<х≤0, то F(х)=Р(Х=-1)=0,1, т.к. в промежуток (-∞; х) попадает только одно значение x₁=-1;

если 0<х≤1, то F(х)=Р(Х=-1)+Р(Х=0)=0,1+0,1=0,2, т.к. в промежуток

(-∞; х) попадают два значения x₁=-1 и x₂=0;

если 1<х≤2, то F(х)=Р(Х=-1)+ Р(Х=0)+Р(Х=1)=0,1+0,1+0,3=0,5, т.к. в промежуток (-∞; х) попадают три значения x₁=-1, x₂=0 и x₃=1;

если 2<х≤3, то F(х)=Р(Х=-1)+Р(Х=0)+Р(Х=1)+Р(Х=2)= 0,1+0,1+0,3+0,2=0,7, т.к. в промежуток (-∞; х) попадают четыре значения x₁=-1, x₂=0,x₃=1 и х₄=2;

если х>3, то F(х)=Р(Х=-1)+Р(Х=0)+Р(Х=1)+Р(Х=2)+Р(Х=3)= 0,1+0,1+0,3+0,2+0,3=1, т.к. в промежуток (-∞; х) попадают четыре значения x₁=-1, x₂=0,x₃=1,х₄=2 и х₅=3.

Итак,

0 при х≤-1,

0,1 при -1<х≤0,

0,2 при 0<х≤1,

F(x)= 0,5 при 1<х≤2,

0,7 при 2<х≤3,

1 при х>3

Изобразим функцию F(x)графически (рис.2):

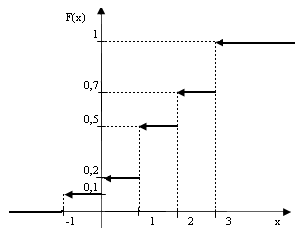
рис. 2

Найдем числовые характеристики случайной величины:

М(Х)=∑ x_κр_κ =x₁р₁ + x₂р₂+…+ x_nр_n

M(X)=-1•0,1+0•0,1+1•0,3+2•0,2+3•0,3=1,5

D(X)= ∑ x²_κр_κ –(M(X))² = x²₁р₁ + x²₂р₂+…+ x²_nр_n –(M(X))²

D(X)=(-1)² •0,1+1²•3+2²•0,2+3²•0,3-(1,5)²=1,65

^≈1,2845.

Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Полученные в результате наблюдения (опыта, эксперимента) данные сначала надо каким-либо образом обработать: упорядочить, представить в удобном для обозрения и анализа виде. Это первая задача. Вторая задача, оценить, хотя бы приблизительно, интересующие нас характеристики наблюдаемой случайной величины. Следующей задачей, является проверка статистических гипотез, т.е. решение вопроса согласования результатов оценивания с опытными данными.

Предметом исследования в математической статистике является совокупность объектов, однородных относительно некоторых признаков. Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях над одним объектом, называется генеральной совокупностью.

Обычно применяют выборочный метод, который заключается в том, что из генеральной совокупности случайным образом извлекают n элементов. Эти элементы называются выборочной совокупностью или выборкой. Количество элементов в выборке называется ее объемом. Исследователь изучает и анализирует выборочную совокупность и на основании полученных показателей делает вывод о параметрах генеральной совокупности.

Допустим, из генеральной совокупности извлечена выборка объемом n, измерена некоторая величина Х, в результате чего получен ряд значений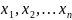 . Этот ряд называется простым статистическим рядом.

Пример. Измерена масса тела 10 девочек 6 лет. Полученные данные образуют простой статистический ряд:

24 22 23 28 24 23 25 27 25 25

Отдельные значения статистического ряда называются вариантами. Если варианта 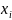появилась m раз, то число m называют частотой, а ее отношение к объему выборки p=m/ n – относительной частотой.

Последовательность вариант, записанная в возрастающем (убывающем) порядке, называется ранжированным рядом.

Пример. Ранжированный ряд: 22 23 23 24 24 25 25 25 27 28

Полученная таким образом последовательность

значений случайной величины называется вариационным рядом.

Существуют характеристики вариационного ряда: меры уровня, или средние. Наиболее употребительными в статистических исследованиях являются три вида средних: средняя арифметическая, мода и медиана.

Cредняя арифметическая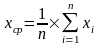

Модой называется варианта, имеющая наибольшую частоту.

Размах – это разность между наибольшим и наименьшим значениями ряда.

Медианой называется варианта, расположенная в центре ранжированного ряда. Если ряд состоит из четного числа вариант, то медианой считают среднее арифметическое двух вариант, расположенных в центре ранжированного ряда.

Выборочная дисперсия

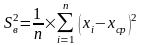
Выборочное стандартное отклонение