5) Метод статистического моделирования на эвм.

Суть данного метода состоит в том, что результат испытания зависит от случайной величины, распределенной по закону (напр. Равномерный, экспотенциальный, нормальный.)

Результат каждого отдельного исследования носит случайный характер. Проведя серию испытаний, получают множество значений наблюдаемой величины.

Погрешность результатов понижается с увеличением числа наблюдений.

Особенностью метода является то, что получаемая в результате моделирования информация по своей природе аналогична той информации, которую можно было бы получить в процессе исследования реальной системы, однако объем ее значительно больший и на ее получение затрачивается меньше средств и времени. Отсюда следует эффективность использования метода моделирования, а также высокая точность и достоверность получаемых с его помощью результатов по сравнению с исследованием реальной системы.

Метод моделирования обычно используется для решения двух классов задач: детерминированных и вероятностных. Наибольший практический интерес представляет применение метода к вероятностным задачам, что позволяет решать задачи, не сформулированные в виде уравнений или формул.

В основе решения на ЭВМ вероятностных задач лежит моделирование случайных явлений. Различные случайные величины, характеризующие отдельные стороны исследуемого процесса, воспроизводятся на ЭВМ с помощью случайных чисел в соответствии с заданными законами распределения.

Теоретической основой метода моделирования служит закон больших чисел. Следовательно, этот метод основан на самых общих теоремах теории вероятностей и принципиально не содержит никаких ограничений.

Достоинства метода.

1.Может быть применен для исследования любой системы с известным аолгоритмом функционирования

2.Можно требовать любой точности

3.Позволяет полнее учесть особенности функционирования исследуемой системы

4.Использует любые законы распледеления

5.Наглядная вероятностная трактовка

6.Простая вычислительная схема, малочувствительная к случайным сбоям ЭВМ

Вместе с тем метод моделирования обладает рядом недостатков, наиболее существенными из которых являются большая трудоемкость и частный характер решения.

6) Зависимые и независимые переменные в модели объекта

Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и образующих в общем случае следующие подмножества:

- совокупность Х - входных воздействий на S хi принадлежит Х, i=1…nx;

- совокупность воздействий внешней среды vl принадлежит V, l=1…nv;

- совокупность внутренних (собственных) параметров системы hk принадлежит H, k=1…nh;

- совокупность выходных характеристик системы yj принадлежит Y, j=1…ny.

При этом в перечисленных подмножествах можно выделить управляемые и неуправляемые переменные. В общем случае х„ vh hk, yj являются элементами непересекающихся подмножеств и содержат как детерминированные, так и стохастические составляющие.

При моделировании системы S входные воздействия, воздействия внешней среды Е и внутренние параметры системы являются независимыми (экзогенными) переменными, которые в векторной форме имеют соответственно вид

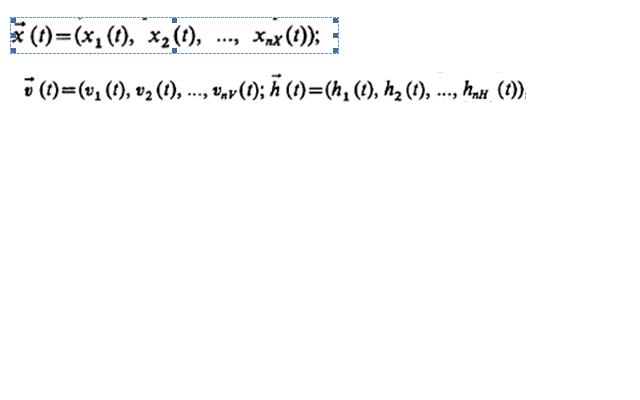
а выходные характеристики системы являются зависимыми (эндогенными) переменными

и в векторной форме имеют вид