- •1) Понятие модели системы
- •2) Сущность системного подхода к моделированию систем па эвм
- •3) Характерные черты машинной модели
- •4) Классификационные признаки видов моделирования систем
- •5) Метод статистического моделирования на эвм.
- •6) Зависимые и независимые переменные в модели объекта
- •7) Типовые схемы при моделирования сложных систем и элементов
- •8) Условия и особенности использования при разработке моделей систем различных типовых схем
- •9) Понятие концептуальной моделью системы
- •10) Основные принципы построения моделирующих алгоритмов процессов функционирования систем.
- •11) Схемы, используемые при разработке алгоритмического и программного обеспечения машинного моделирования
- •12) Техническая документация, оформляемая по каждому этапу моделирования системы
- •13) Сущность метода статистического моделирования систем
- •14) Способы генерации последовательностей случайных чисел, используемые при моделировании.
- •15) Методы проверки (тестирования) качества генераторов случайных чисел.
- •16) Способы генерации последовательностей случайных чисел с заданным законом распределения на эвм
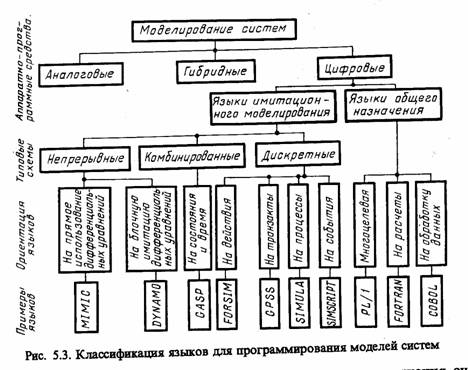
- •17) Языки имитационного моделирования. Архитектура, основные требования, группы языков моделирования дискретных систем
- •18) Особенности машинного эксперимента
- •19) Виды факторов в имитационном эксперименте с моделями систем
- •20) Полный факторный эксперимент
- •21) Сущность методов фиксации и обработки результатов при статистическом моделировании систем на эвм
- •24) Синхронный и асинхронный моделирующие алгоритмы q-схем.
- •25) Суть структурного подхода при моделировании систем на базе n-схем
- •26) Особенности использования языков имитационного моделирования на базе n-схем
- •27) Особенности формализации процессов функционирования систем на базе а-схем
- •28) Информационная модель системы.
- •29) Эволюционные модели систем
- •30) Модели для принятия решения
15) Методы проверки (тестирования) качества генераторов случайных чисел.




16) Способы генерации последовательностей случайных чисел с заданным законом распределения на эвм
Пусть непрерывная случайная величина η определена в интервале (а,b) и имеет плотность распределения f(x)>0 при а<х<b (случай а = - ∞ , b = ∞ не исключается).
функция распределения: Fx=axf(x)dx
Принцип работы метода обратной функции сформулируем в виде теоремы 6.1. Случайная величина η, реализации х которой определяются из выражения
F (x)=z или x=F-1 (z), (6.14)
где z - реализация базовой случайной величины ξ, имеет плотность распределения f(x).
Доказательство. Напишем выражение для вероятности попадания случайной величины ξ в отрезок [0, z]
Pξ≤z=PFη≤Fx=Pη≤x=Fx=z (6.15)
Первое равенство выражения (6.15) написано из условия (6.14) данной теоремы. Справедливость второго равенства следует из свойства монотонного возрастания функции распределения от нуля до единицы. И, наконец, последнее равенство предопределено известным свойством равномерного распределения, что вероятность попадания случайной величины в некоторый интервал, равна длине этого интервала, т.е. Р { ξ < z} = z.
Для практического применения метода обратной функции необходимо разрешить относительно х уравнение: ax1fxdx=zj (6.16)
Пример 1. Случайная величина η с функцией плотности f(x)=x-2 определена на интервале [1, ∞). Воспользовавшись соотношением (3.3), можно получить ax1x-2dx=1-1xj=zj тогда xj=F-1zj=1(1-zj)
Алгоритм, реализующий метод обратной функции, состоит из следующих процедур:
Шаг 1. Положить у =1.
Шаг 2. Получить реализацию z случайной величины ξ.
Шаг 3. Вычислить реализацию х случайной величины η. xj=F-1(zj)
Шаг 4. Положить j=j+1
Шаг 5. Проверить выполнение условия j>n, где n – требуемое число реализаций случайной величины η. При нарушении этого условия переход на шаг 2.
Шаг 6. Вывод значений {xj}..
17) Языки имитационного моделирования. Архитектура, основные требования, группы языков моделирования дискретных систем
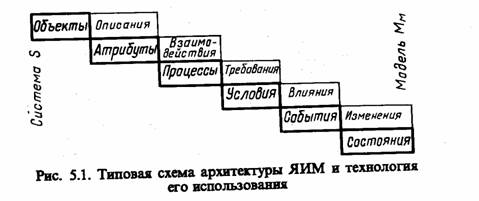
рхитектуру ЯИМ, т. е. концепцию взаимосвязей элементов языка как сложной системы, и технологию перехода от системы S к ее машинной модели Мы можно представить следующим образом: 1) объекты моделирования (системы S) описываются (отображаются в языке) с помощью некоторых атрибутов языка; 2) атрибуты взаимодействуют с процессами, адекватными реально протекающим явлениям в моделируемой системе S; 3) процессы требуют конкретных условий, определяющих логическую основу и последовательность взаимодействия этих процессов во времени; 4) условия влияют на события, имеющие место внутри объекта моделирования (системы 5) и при взаимодействии с внешней средой Е; 5) события изменяют состояния модели системы М в пространстве и во времени.
Типовая схема архитектуры ЯИМ и технология его использования при моделировании систем показана на рис. 5.1.
Требования к языкам имитационного моделирования. Таким образом, при разработке моделей систем возникает целый ряд специфических трудностей, поэтому в ЯИМ должен быть предусмотрен набор таких программных средств и понятий, которые не встречаются в обычных ЯОН.
Совмещение. Параллельно протекающие в реальных системах S процессы представляются с помощью последовательно работающей ЭВМ. Языки моделирования позволяют обойти эту трудность путем введения понятия системного времени, используемого для представления упорядоченных во времени событий.
Размер. Большинство моделируемых систем имеет сложную структуру и алгоритмы поведения, а их модели велики по объему. Поэтому используют динамическое распределение памяти, когда компоненты модели системы Мм появляются в оперативной памяти ЭВМ или покидают ее в зависимости от текущего состояния. Важным аспектом реализуемости модели Мм на ЭВМ в этом случае является блочность ее конструкции, т. е. возможность разбиения модели на блоки, подблоки и т. д.
Изменения. Динамические системы связаны с движением и характеризуются развитием процесса, вследствие чего пространственная конфигурация этих систем претерпевает изменения по времени. Поэтому во всех ЯИМ предусматривают обработку списков, отражающих изменения состояний процесса функционирования моделируемой системы S.
Взаимосвязанность. Условия, необходимые для свершения различных событий в модели Мм процесса функционирования системы S, могут оказаться весьма сложными из-за наличия большого количества взаимных связей между компонентами модели. Для разрешения связанных с этим вопросом трудностей в большинство ЯИМ включают соответствующие логические возможности и понятия теории множеств.
Стохастичность. Для моделирования случайных событий и процессов используют специальные программы генерации последовательностей псевдослучайных чисел, квазиравномерно распределенных на заданном интервале, на основе которых можно получить стохастические воздействия на модель Мм, имитируемые случайными величинами с соответствующим законом распределения.
Анализ. Для получения наглядного и удобного в практическом отношении ответа на вопросы, решаемые методом машинного моделирования, необходимо получать статистические характеристики процесса функционирования модели системы M(S). Поэтому предусматривают в языках моделирования способы статистической обработки и анализа результатов моделирования.