4. Способы квантования.
Непрерывный
сигнал в системе координат
описывается в непрерывной функции
.
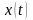Переход от аналогового представления сигнала к цифровому, который дает в ряде случаев значительное преимущество при передаче, хранении и обработки информации, связан с квантованием (дискретизацией) сигнала по времени и по уровню.
Разновидность сигналов, которые описываются функцией .
Непрерывная
функция непрерывного аргумента (а).
Значения функции
,
и аргумент
заполняют конечные (или бесконечные)
промежутки
и
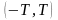соответственно.
Непрерывная
функция дискретного аргумента (б). Здесь
значения функции
определяются на дискретном множестве
значений аргумента
.
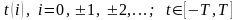Величина
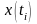может принимать любое значение на
отрезке
.
Дискретная
функция непрерывного аргумента (в). В
этом случае значения, которые может
принимать функция
,
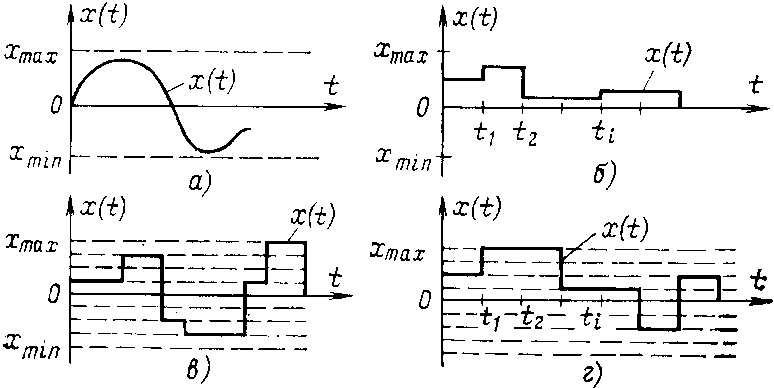
образуют дискретный ряд чисел
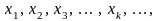т.е. такой конечный или бесконечный ряд,
в котором каждому числу
можно поставить соответствие интервал
,
внутри которого других чисел одного
ряда нет. Значения аргумента
может быть любым на
.
Дискретная
функция дискретного аргумента (г).
Значения, которые может принимать
функция
,
и аргумент
образуют дискретный ряд чисел
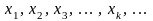и
,
заполняющие отрезки
и
соответственно.
Обычно
операцию, переводящую непрерывный
сигнал в дискретно-непрерывный, называют
квантованием по времени или дискретизацией.
Следовательно, дискретизация состоит
в преобразовании сигнала
непрерывного аргумента
в сигнал
дискретного аргумента
.
Квантование
по уровню состоит в преобразовании
непрерывного множества значений сигнала
в дискретное множество значений
,
.
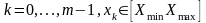Совместное
применение операций дискретизации и
квантования позволяет преобразовать
непрерывный сигнал
в дискретный по координатам
и
.
Дискретизация
реализации сигнала
связано с заменой промежутка измерения
независимой переменной некоторым
множеством точек, т.е. операции
дискретизации соответствует отображение
(5.1), где
- функция, описывающая сигнал;
- функция, описывающая сигнал, полученный
в результате дискретизации.
По
значением функции
можно восстановить исходную функцию
с некоторой погрешностью. Функцию,
полученную в результате восстановления
(интерполяции) по значениям функции
,
называют воспроизводящей
.
Воспроизводящая функция
строится как взвешенная сумма некоторого
ряда функций
.
(5.2) причем коэффициенты
зависят от отсчетов
,
.
При обработке сигналов дискретизация по времени должна производиться таким образом, чтобы по отсчетным значениям функции можно было получить воспроизводящую функцию , которая с заданной точностью отображает исходную функцию .
При
дискретизации сигналов приходится
решать вопрос, каков должен быть шаг
дискретизации
.
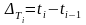При малых шагах дискретизации
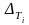количество отсчетов функции на отрезке
обработки будет большим и точность
воспроизведения высокой.
При больших шагах дискретизации количество отсчетов уменьшится, но при этом, как правило, снижается точность восстановления.
Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве выборов. В этом случае все отсчеты существенны для восстановления исходного сигнала.
Методы дискретизации и восстановления сигналов можно разделить на несколько групп в зависимости от принятых признаков классификации:
1. Регулярность отсчета (равномерные, неравномерные, случайные, адаптивные, с кратными и некратными интервалами).
2. Критерий оценки точности дискретизации и восстановления (максимальный, среднеквадратичный, интегральный, вероятностный).
3. Базисные функции (ряд Фурье, Котельникова, полиномы Чебышева, Лежандра, степенные полиномы, функции Уолша, Хаара, гипергеометрические).
4. Принцип приближения (интерполяция, экстраполяция, комбинированный).