Тематическая структура АПИМ
№ ДЕ |
Наименование дидактической единицы ГОС |
№ задания |
Тема задания |
1 |
?? |
1 |
Случайные величины |
2 |
Законы распределения |
||
2 |
?? |
3 |
Основы вероятностной теории информации |
4 |
Метод Монте-Карло |
||
5 |
Моделирование случайных величин с заданными законами распределения |
||
3 |
?? |
6 |
Основные понятия теории случайных процессов |
7 |
Основные виды потоков: простейший поток, поток Пальма |
||
8 |
Системы массового обслуживания |
||
4 |
?? |
9 |
Элементы теории управления запасами |
10 |
Элементы теории надежности |
||
11 |
Элементы статического анализа временных рядов |
«1.??????????: 1.1 Случайные величины» «1.??????????: 1.2 законы распределения» «2.??????????: 2.3 Основы вероятностной теории информации»
Для
дискретных случайных величин
заданных законами распределения
,
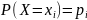и совместным распределением
,
количество информации, содержащейся в
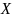относительно
:
*
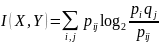
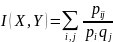
Количество информации, содержащееся в Х относительно Х:
*
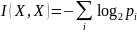
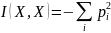
Энтропия случайной величины равна нулю, если
величина нормально распределена
*величина является постоянной
величина экспоненциально распределена
Случайная величина X является функцией от случайной величины Y, если
*
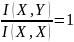
Энтропия случайной величины имеет вид
*
Наука, изучающая количественные закономерности, связанные с получением, передачей, обработкой и хранением информации
*теория информации
теория закономерностей
теория количественных закономерностей
информатика
Сумма произведений вероятностей различных состояний системы на логарифмы этих состояний, взятая с обратным знаком
*энтропия системы
дисперсия системы
математическое ожидание системы
Полная информации о системе X, содержащаяся в системе Y
*всегда отрицательна
всегда отрицательна
может быть как положительной, так и отрицательной
Уменьшение неопределенности касательно исхода опыта в результате его осуществления понимается в вероятностной теории как
*получение информации
хранение информации
передача информации
переработка информации
Формула энтропии системы
*
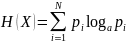
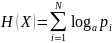
Если вероятность наступления некоторого события в опыте равна единице, то энтропия этого события равна
*нулю
единице
плюс бесконечности
минус бесконечности
Энтропия конечного множества случайных событий представляет собой математическое ожидание величины
*
Свойства
меры количества информации
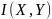
*она равна нулю, если события множества и независимы
*достигает максимума, когда события множества достоверно отражают события множества
*больше нуля, при зависимости событий множеств
меньше нуля, при зависимости событий множеств
Кем была разработана вероятностная теория информации
*Клодом Шенноном
Эндрю Танненбаумом
Альфредом Реньи
Андреем Колмогоровым
«2.??????????: 2.4 Метод монте-карло»
Погрешность метода Монте-Карло определяет
*доверительный интервал для математического ожидания
доверительный интервал для СКО
доверительный интервал для дисперсии
В
способе усреднения подынтегральной
функции, в качестве оценки интеграла
принимают
*
В способе, основанном на истолковании интеграла как площади, в качестве оценки интеграла принимают
*
В способе существенной выборки, использующий «вспомогательную плотность распределения» в качестве оценки интеграла принимают
*
Какие последовательности случайных чисел называются псевдослучайными?
*последовательности случайных чисел, вырабатываемые детерминистскими способами
последовательности случайных чисел, вырабатываемые стохастическими способами
последовательности случайных чисел, вырабатываемые дискретными способами
Что означают термины “случайные числа” и “последовательность случайных чисел”?
что каждое число было получено самым произвольным образом, с учетом взаимной связи с другими членами последовательности, и что у него есть определенная вероятность отказаться в заданном интервале
*что каждое число было получено самым произвольным образом, без всякой связи с другими членами последовательности, и что у него есть определенная вероятность оказаться в заданном интервале
что каждое число было получено самым произвольным образом, с учетом взаимной связи с другими членами последовательности, и оно точно окажется в заданном интервале
что каждое число было получено самым произвольным образом, с учетом взаимной связи с другими членами последовательности, и оно точно окажется в заданном интервале