- •Атомная Физика.
- •Глава I. Корпускулярно – волновой дуализм электромагнитных волн.
- •§ 1.1. Фотоэффект.
- •§ 1.2. Эффект Комптона.
- •§ 1.3. Интерференция фотонов.
- •§ 1.4. Дифракция рентгеновских лучей в кристаллах.
- •§ 1.5. Волновые свойства корпускул.
- •Глава II. Дискретность электронных и атомных состояний.
- •§ 2.1. Законы излучения абсолютно чёрного тела.
- •§ 2.2. Экспериментальное подтверждение дискретной природы энергетических уровней атомов и молекул.
- •§ 2.3. Спектры испускания и поглощения атомов.
- •§ 2.4. Ядерная модель атома.
- •Глава III. Основные положения квантовой механики
- •§ 3.1. Основные сведения из теории операторов.
- •§ 3.2. Постулаты квантовой механики. Представление динамических переменных.
- •§ 3.3. Соотношение неопределённостей Гейзенберга.
- •§ 3.4. Соотношение неопределённостей произвольных физических величин. Принцип дополнительности.
- •§ 3.5. Понятие представления в квантовой механике.
- •Глава IV. Простейшие случаи движения микрочастиц.
- •§ 4.1. Свободное движение частиц.
- •§ 4.2. Частица в одномерной потенциальной яме.
- •§ 4.3. Прохождение частицы через потенциальный барьер.
- •§ 4.4. Линейный гармонический осциллятор.
- •§ 4.5. Движение в поле центральных сил.
- •Глава V. Теория атома водорода и водородоподобных атомов.
- •§ 5.1. Стационарные состояния.
- •§ 5.2. Атомы щелочных металлов.
- •§ 5.3. Магнитный и механический момент электрона.
- •§ 5.4. Векторная модель атома. Правила сложения моментов.
- •§ 5.5. Типы связи электронов в атоме.
- •§ 5.6. Полный магнитный момент атома.
- •§ 5.7. Магнитомеханические эффекты.
- •§ 5.8. Экспериментальные методы определения магнитного момента.
- •Глава VI. Взаимодействие атома с электромагнитным полем.
- •§ 6.1. Эффект Зеемана.
- •§ 6.2. Эффект Пашена – Бака.
- •§ 6.3. Эффект Штарка.
- •Глава VII. Структура и спектр сложных атомов.
§ 5.6. Полный магнитный момент атома.
Полный магнитный момент атома складывается
из полных спинового и орбитального
моментов атома:
![]() .
Для каждого из них мы можем записать:
.
Для каждого из них мы можем записать:![]() и
и
![]() .
Таким образом, полный механический
момент не будет лежать на одной оси с
полным механическим моментом.
.
Таким образом, полный механический
момент не будет лежать на одной оси с
полным механическим моментом.
Рассмотри случай изолированного атома.
В изолированном атоме
![]() .
Если вектор
.
Если вектор
![]() сохраняет своё направление в пространстве,
вектора
сохраняет своё направление в пространстве,
вектора
![]() и
и
![]() должны
прецессировать вокруг
.
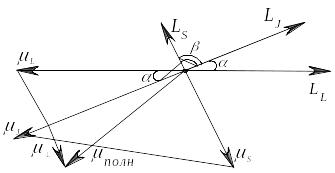
Следовательно, прецессируют и полные
механический и магнитный моменты. Из
рисунка 55 видно,
должны
прецессировать вокруг
.
Следовательно, прецессируют и полные
механический и магнитный моменты. Из
рисунка 55 видно,
![]() и прецессирует вокруг оси
.
и прецессирует вокруг оси
.
![]() – проекция
– проекция
![]() на
и
на
и
![]() .
Для достаточно большого промежутка
времени среднее значение
.
Для достаточно большого промежутка
времени среднее значение
![]() ,
поэтому
,
поэтому
|
Рис. 55 |
![]() .
Таким образом, если на языке моментов
описывать магнитоэлектрические
(оптические) эффекты, можно пользоваться
.
Найдём связь между
и
.
Таким образом, если на языке моментов
описывать магнитоэлектрические
(оптические) эффекты, можно пользоваться
.
Найдём связь между
и
![]() .
Из рисунка 55 видно, что
.
Из рисунка 55 видно, что
![]() (1).
(1).
![]() (2),
(2),
![]() .
Следовательно,
.
Следовательно,
![]() .
Найдём
.
Из уравнения (2) следует, что
.
Найдём
.
Из уравнения (2) следует, что
![]() ,
,
![]() ;
;
![]() .
Запишем уравнения для проекции магнитного
момента на направление вектора
:
.
Запишем уравнения для проекции магнитного
момента на направление вектора
:
![]()
![]() .
.
Подставим последние два выражения в (1) с учётом полученных выше выражений для косинусов:
![]()
Подставим значения для каждого момента, выраженное через квантовые числа:

Выражение ,
помещённое в круглых скобках, называется
фактором Ланде:
![]() .
Таким образом,
.
Таким образом,
![]() (3). Выражение (3) аналогично тому,
которое связывает спиновой орбитальный
момент с орбитальным механическим. Из
этой аналогии следует смысл фактора
Ланде – это гиромагнитное отношение
для полного магнитного момента. В
частности, получается, что если спиновое
квантовое число равно нулю, то
(3). Выражение (3) аналогично тому,
которое связывает спиновой орбитальный
момент с орбитальным механическим. Из
этой аналогии следует смысл фактора
Ланде – это гиромагнитное отношение
для полного магнитного момента. В
частности, получается, что если спиновое
квантовое число равно нулю, то![]() ,
тогда
,
тогда
![]() .
Если же магнитный момент обусловлен
спиновым движением, то есть
.
Если же магнитный момент обусловлен
спиновым движением, то есть
![]() ,
то
,
то
![]() ,
а
,
а
![]() .
.
§ 5.7. Магнитомеханические эффекты.
В предыдущем параграфе мы показали, что существует связь между полным магнитным и механическим моментами. Если ориентация магнитного момента в пространстве, изменяется, то, чтобы выполнялось соотношение (3) предыдущего параграфа: , должна изменяться ориентация механического момента. Явления, обусловленные связью механического и магнитного моментов, называют магнитомеханическими эффектами.
Пусть некоторый
магнетик намагничен. Это значит, что
все магнитные моменты атомов ориентированы
в направлении намагничивания. Это
приводит к тому, что и все механические
моменты атомов будут стремиться
ориентироваться определённым образом:
 ,
,
![]() ,
где
,
где
![]() ,
,
![]() .
Итак, при изменении магнитного момента
образца, изменяется его механический
момент так, чтобы их сумма всегда
оставалась постоянной. Это значит, что
при намагничивании образца он приобретёт
дополнительный момент импульса. Для
обнаружения магнитомеханических
эффектов Эйнштейном и де Гаазом на
тонкой упругой нити подвешивался
цилиндр. Его помещали в
.
Итак, при изменении магнитного момента
образца, изменяется его механический
момент так, чтобы их сумма всегда
оставалась постоянной. Это значит, что
при намагничивании образца он приобретёт
дополнительный момент импульса. Для
обнаружения магнитомеханических
эффектов Эйнштейном и де Гаазом на
тонкой упругой нити подвешивался
цилиндр. Его помещали в
|
Рис. 56 |
продольное
магнитное поле, которое создавалось
соленоидом, охватывающим образец.
Магнитный и механический моменты связаны
соотношением:
![]() .
.
![]() – полный механический момент образца.
Так как образец изолирован, то закон
сохранения момента импульса должен
выполнятся. Полный момент импульса
будет складываться из механического
момента образца полного собственного
механического момента всех электронов:
– полный механический момент образца.
Так как образец изолирован, то закон
сохранения момента импульса должен
выполнятся. Полный момент импульса
будет складываться из механического
момента образца полного собственного
механического момента всех электронов:
![]() .
Тогда,
.
Тогда,
![]() ,
,
![]() .
Переходя к конечным приращениям, получим
.
Переходя к конечным приращениям, получим
![]() .
Но
.
Но
![]() .
Поэтому
.
Поэтому
![]() .
Момент импульса образца равен
.
Момент импульса образца равен
![]() ,
где
– момент инерции. Кинетическая энергия
вращательного движения твёрдого тела,
как известно из механики, равна:
,
где
– момент инерции. Кинетическая энергия
вращательного движения твёрдого тела,
как известно из механики, равна:
![]() ,
а её изменение –
,
а её изменение –
![]() .
.
Обозначим
модуль упругости нити. Тогда при её
закручивании на угол
потенциальная энергия нити будет
![]() .
По закону сохранения энергии
.
По закону сохранения энергии
![]() ,
,
![]() ,
,
![]() .
Если
.
Если
![]() – собственная частота колебания образца,
то она связана с модуле упругости
кручения нити и моментом инерции
следующим соотношением:
– собственная частота колебания образца,
то она связана с модуле упругости
кручения нити и моментом инерции
следующим соотношением:
![]() .
Следовательно,
.
Следовательно,
![]() .
Тогда,
.
Тогда,
![]()
![]() ,
т. о. Зная модуль упругости нити,
собственную частоту колебаний образца
и угол закручивания нити можно определить
,
т. о. Зная модуль упругости нити,
собственную частоту колебаний образца
и угол закручивания нити можно определить
![]() ,
а значит и
.
Эйнштейн и де Гааз получили, что
ферромагнитных цилиндров
.
Это значит1,
что магнетизм обусловлен спиновым
движением электронов.
,
а значит и
.
Эйнштейн и де Гааз получили, что
ферромагнитных цилиндров
.
Это значит1,
что магнетизм обусловлен спиновым
движением электронов.
Эффектом обратным
эффекту Эйнштейна – де Гааза является
эффект Барнета. Рассмотрим поведение
атома в магнитном поле. На магнитный
момент
атома в этом поле действует момент сил:
![]() .
Но атом обладает механическим моментом
и поэтом ведёт себя как гироскоп. Под
влиянием этого момента силы, будет
задаваться
.
Чтобы соотношение
.
Но атом обладает механическим моментом
и поэтом ведёт себя как гироскоп. Под
влиянием этого момента силы, будет
задаваться
.
Чтобы соотношение
|
Рис. 57 |
Между ними сохранялось, будет происходить прецессия механического момента атома вокруг заданного направления (не вокруг !!!). Это направление будет направлением вектора . По
|
Рис. 58 |
второму
закону Ньютона для проекций векторов
мы можем записать:
 так как
так как
![]()
![]() .
В векторной форме
.
В векторной форме
![]() .
Но
.
Но
![]() .
Тогда
.
Тогда
 ,
где
,
где
![]() – частота прецессии механического
момента вокруг направления магнитного
поля. Если фактор Ланде для атома равен
– частота прецессии механического
момента вокруг направления магнитного
поля. Если фактор Ланде для атома равен
![]() ,
то есть магнетизм атома обеспечивает
орбитальный магнитный момент электронов
(спин равен нулю), то
,
то есть магнетизм атома обеспечивает
орбитальный магнитный момент электронов
(спин равен нулю), то
![]() ,
то есть частота прецессии равна прецессии
орбитального момента:
,
то есть частота прецессии равна прецессии
орбитального момента:
![]() – ларморовой частоте прецессии. Благодаря
прецессии всех атомов в магнитном поле
в одном и том же направлении возникает
дополнительный магнитный момент, что
приводит к намагничиванию образца. В
этом состоит суть эффекта Барнета.
– ларморовой частоте прецессии. Благодаря
прецессии всех атомов в магнитном поле
в одном и том же направлении возникает
дополнительный магнитный момент, что
приводит к намагничиванию образца. В
этом состоит суть эффекта Барнета.