Теория вероятностей Лекция 1 Случайные явления

Все явления окружающего нас мира взаимно связаны и влияют одно и другое (закон всеобщей связи явлений). Каждое наблюдаемое явление связано причинной зависимостью с бесчисленным множеством других явлений и течение его зависит от бесчисленного множества факторов. Проследить все это множество связей невозможно. Поэтому при изучении реального явления ограничиваются лишь основными факторами, при этом явление заменяется упрощенной схемой, для которой устанавливают закономерности. Наблюдаемые в реальном явлении отклонения от закономерностей, вызванные совместным действием бесчисленного множества неучтенных факторов, представляет собой случайное явление.

Примеры случайных явлений.

1.Экспериментальные данные на графике никогда не ложатся на одну кривую, а заполняют некоторую полосу, т.е. имеет место случайный разброс экспериментальных точек.

2. При стрельбе, если прицеливание ведется по одной точке, снаряды никогда не ложатся в одну точку, так как аэродинамические силы и их моменты, действующие на снаряд, зависят от множества факторов, в частности от состояния атмосферы во всех точках траектории. Поэтому происходит рассеивание снарядов.

3. Отказы различных технических устройств.

4. Шумы при приеме радиопередач.

При многократном наблюдении случайных явлений в них можно заметить некоторые закономерности. Изучение этих закономерностей дает возможность в известной степени управлять этими явлениями, предсказывать результаты их действия и целенаправленно использовать их в практической деятельности.

Теория вероятностей занимается изучением закономерностей массовых случайных явлений, т.е. таких, которые можно наблюдать много (в идеале бесчисленное множество раз). Теория вероятностей является мощным инструментом исследования и поэтому находит применение в различных областях науки и инженерной практики: физике, аэродинамике, гидродинамике, радиотехнике, теории управления, связи, строительной механике теории машин и механизмов, теории волнения и качки кораблей, метеорологии.

Элементарная часть теории вероятностей в значительной мере опирается на комбинаторику

Элементы комбинаторики

Комбинаторикой называют область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Общие правила комбинаторики

Правило суммы

Пусть выбираются два объекта и . Ни один из способов выбора объекта не совпадает ни с одним способом выбора объекта , то есть нельзя выбрать и одним и тем же способом. Тогда, если объект можно выбрать способами, а объект можно выбрать способами, то выбор " " ( ) можно осуществить способами.

Правило произведения

Пусть выбираются два объекта и . Количество способов выбора объекта не зависит от количества способов выбора объекта .

Тогда, если объект можно выбрать способами, а другой объект после выбора А можно выбрать способами, то выбор пары ( ) в указанном порядке можно осуществить способами.

Пусть требуется выполнить одно за другим действий. Если первое действие можно выполнить способами, второе действие можно выполнить способами, …, действие можно выполнить способами, то все действий могут быть выполнены способами.

Пример.

Из Москвы до Твери добраться пароходом, поездом, автобусом, самолетом. Из Твери до Кашина можно добраться самолетом или автобусом. Из Москвы до Кашина, минуя Тверь, можно также добраться автомобилем или вертолетом. Сколькими способами можно осуществить путешествие по маршруту Москва- Кашин?

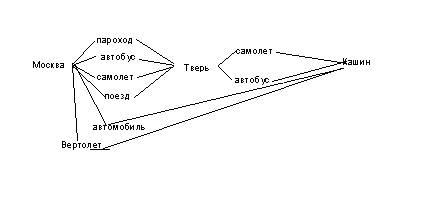
Число способов равно .

Конечное -элементное множество называется упорядоченным, если каждому элементу множества поставлено в соответствие некоторое натуральное число – номер элемента, причем различным элементам соответствуют различные числа.