2. Методичний інструментарій оцінки вартості грошей на основі використання простого відсотку
Схема простих відсотків може використовуватись при короткостроковому інвестуванні , а також в практиці банківських розрахунків при нарахуванні відсотків по короткостроковим позичкам зі строком погашення до одного року.
Простим відсотком називається сума, яка нараховується від первісної суми вкладу в кінці одного періоду платежу. Наглядно механізм нарахування відсотків по схемі простих відсотків показано в таблиці 2.1.1.
Таблиця 2.1.1.
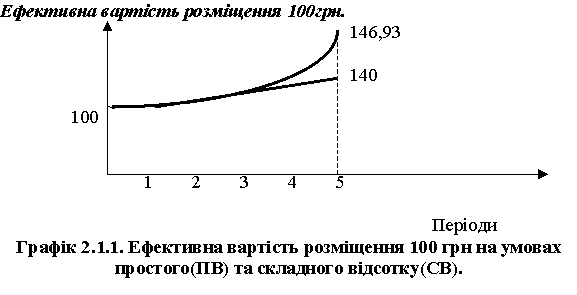
Вартість 100 грн., що розміщені під 8% (простих)на n періодів.
Роки |
Під простий відсоток 100+100*і*n |
1 |
100+8=108 |
2 |
108+8=116 |
3 |
116+8=124 |
4 |
124+8=132 |
5 |
132+8=140 |
Отже, вважається, що інвестиція здійснена на умовах простого відсотку, якщо вкладена сума грошових коштів щорічно збільшується на величину (Р * і), де Р – інвестована сума грошових коштів, i – процентна ставка
При використанні схеми простих відсотків може бути визначено:
Майбутня вартість вкладу(FV):
FV = PV*(1+i*n)
Де i – процентна ставка, n – кількість інтервалів , по яких здійснюється розрахунок процентних платежів в загальному обумовленому періоді часу.
В даному випадку вираз (1+i*n) називається множник нарощування суми простих відсотків.
Теперішня (приведена) вартість вкладу(PV):
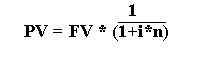
В даному
випадку вираз
називається
дисконтним
множником суми простих відсотків.
Сума простого відсотку в процесі нарощування(І):
І = Р*і*n
Сума дисконту (D):
4. Методичний інструментарій оцінки вартості грошей на основі використання складного відсотку
Схема складного відсотка використовується, як правило, в більшості фінансових розрахунків, якщо не обумовлено, що мова йде про просту процентну ставку. Така схема використовується, в основному, при довгострокових фінансових операціях.
Складним відсотком називається сума доходу, яка утворюється в результаті інвестування за умови, що сума нарахованого відсотка не виплачується після кожного періоду, а приєднується до основної суми вкладу і в наступному платіжному періоді сама приносить доход. В таблиці 2.1.2. показано механізм нарахування відсотків за схемою складних відсотків.
Таблиця 2.1.2.
Вартість розміщення 100 грн. Під 8% (складних) річних на n періодів.
Роки |
Під складні відсотки :100*(1+і)n |
1 |
100+8=108 |
2 |
108+8,64=116,64 |
3 |
116,64+9,33= 125,97 |
4 |
125,97+10,08=136,05 |
5 |
136,05+10,88=146,93 |
Як бачимо, сума процентів, що нараховуються при використанні схеми складного відсотку, щорічно зростає на відміну від простого відсотку. Ця різниця майже не помітна в перші роки, але стає досить значною при більших термінах розміщення коштів. Дані таблиць 2.1.1. і 2.1.2. відображені на графіку 2.1.1. І наглядно показують різницю між цими двома схемами.
При використанні схеми складних відсотків також можна розрахувати:
Майбутню вартість вкладу(FV):
FV = PV * (1+і)n
де PV – приведена(теперішня) вартість, і – процентна ставка за кожний період, n – кількість періодів нарахування відсотка.
Вираз (1+і)n представляє собою множник нарощування суми складних відсотків або відсотковий фактор майбутньої вартості. Його значення можна знайти в спеціальних таблицях, що полегшує процес розрахунків.
Вже зазначалось, що стандартним інтервалом нарахування є один рік. Але на практиці можливе застосування схеми нарощування з внутрішньо річними нарахуванням. В цьому випадку нарахування робляться декілька разів на рік, тоді майбутня вартість має визначатись так:
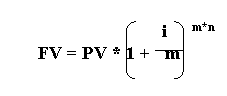
де m – кількість нарахувань на протязі року, n – кількість років.
Розглянемо приклад: 15000 грн. покладено на депозит під 35% річних за умови щоквартального нарахування відсотку. Період нарахування - три роки при умові використання схеми складних відсотків. Знайти майбутню вартість цієї суми грошових коштів через три роки.
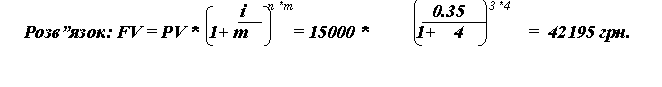
Для розрахунку можна скористатися й таблицею відсоткового фактору майбутньої вартості. Вона наведена в підручнику “Основи фінансового менеджменту” Бланк І.А. с.327, том 2. Знаходимо вже готове значення відсоткового фактору майбутньої вартості грошових коштів на перетині рядку з числом інтервалу = 12 (тому що протягом загального періоду нарахування відсоток буде нараховуватись 12 разів = 3 роки * 4 квартали ) та колонки із нашим значенням ставки відсотка, яка дорівнює приблизно 9%, виходячи з нашої умови (35% : 4 = 8,75 = 9%). Отже, значення відсоткового фактору майбутньої вартості дорівнює 2,813. Майбутня вартість грошового вкладу = 15000*2,813 = 42195 грн.
Теперішню(приведену) вартість вкладу (PV):
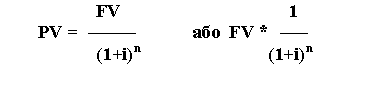
Вираз 1/(1+і)n є не що інше, як множник дисконтування суми складних відсотків або процентний фактор теперішньої вартості. Його значення розраховані в спеціальних таблицях відсоткового фактору теперішньої вартості грошового вкладу, за допомогою яких можна облегшувати процес розрахунків (див. підручник “Основи фінансового менеджменту”, І.А.Бланк, с.331). Механізм використання цих таблиць аналогічний механізму використання таблиць відсоткового фактору майбутньої вартості грошового вкладу.
Приклад: Розрахувати, яку суму потрібно покласти на депозитний рахунок, щоб через два роки мати 1500 грн. Відсоткова ставка становить 16% річних з нарахуванням відсотка раз в півріччя. Застосовується схема складних відсотків.
Розв”язок: Розрахунки легко провести за допомогою розрахункової таблиці відсоткового фактору теперішньої вартості: знаходимо значення відсоткового фактору теперішньої вартості на перетині відповідного рядка (число інтервалів нарахування = 2*2= 4) та колонки ( ставка відсотка = 15% : 2 = 8%). Отже значення відсоткового фактору теперішньої вартості дорівнює 0,735. Далі розраховуємо теперішню вартість вкладу:
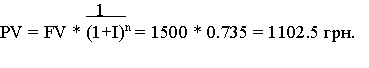
Процентну ставку, що використовується в розрахунках вартості вкладів по складних відсотках(і):
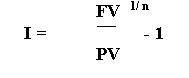
Справа в тому, що різними видами фінансових контрактів можуть передбачатися різні схеми нарахування відсотків. Для забезпечення порівняльного аналізу ефективності таких контрактів і існує власне відносно універсальний показник - ефективна (порівняльна) процентна ставка (іеф), яка характеризує середньорічний її рівень, що визначається співвідношенням річної суми відсотку, нарахованого за періодичними ставками, до основної суми вкладу:
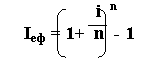
де і – річна ставка відсотка, за якою здійснюється нарахування, n – кількість інтервалів нарахування відсотка впродовж загального періоду нарахування.
Приклад: підприємство має дві альтернативи отримання позики:
А) на умовах щоквартального нарахування відсотків при ставці 75% річних;
Б) на умовах нарахування відсотків раз в півріччя при ставці 80% річних.
Відносні витрати підприємства по обслуговуванню позики можуть бути визначені за допомогою розрахунку ефективної річної ставки – чим вона вища, тим більший рівень витрат:
А) іеф = (1+0,75/4)4 –1 = 0,99
Б) іеф = (1+0,80/2)2 –1 = 0,96
Отже, варіант Б є більш привабливим для підприємства.