
- •Тема 1. Стационарное уравнение
- •1.1. Решение задачи Дирихле для круга методом Фурье
- •Задачи для самостоятельного решения
- •1.2. Решение краевых задач в шаре с использованием сферических функций
- •Задачи для самостоятельного решения
- •1.3. Метод функции Грина
- •Задачи для самостоятельного решения
- •Тема 2. Прямые методы математической физики
- •2.1. Решение задачи Дирихле для уравнения Пуассона методом Ритца
- •2.2. Решение задачи Дирихле для уравнения Пуассона методом Галеркина
- •Типовой расчет
- •Тема 3. Интегральные уравнения
- •3.1. Интегральные уравнения Вольтерра второго рода. Решение интегральных уравнений с помощью резольвенты
- •Задачи для самостоятельного решения
- •3.2. Метод последовательных приближений
- •Задачи для самостоятельного решения
- •3.4. Метод определителей Фредгольма
- •Задачи для самостоятельного решения
- •Библиографический список
- •Содержание
- •Для заметок
2.2. Решение задачи Дирихле для уравнения Пуассона методом Галеркина
Для решения краевой задачи (2.1) здесь применяется проекционный метод Галеркина (см. подробнее [1], п. 2.3.)
Построим множество
дважды непрерывно дифференцируемых в
![]() функций
функций
![]() ,
равных нулю на границе
,
и введем в
скалярное произведение
,
равных нулю на границе
,
и введем в
скалярное произведение
![]() по формуле (2.2). Будем называть функции
по формуле (2.2). Будем называть функции
![]() ортогональными, если их скалярное
произведение равно нулю.
ортогональными, если их скалярное
произведение равно нулю.
Заменим краевую задачу (2.1) эквивалентным уравнением (2.3). Выберем в какую-либо координатную систему (2.6) и будем искать приближенное решение задачи в виде линейной комбинации первых координатных функций
![]() . (2.14)
. (2.14)
Рассмотрим невязку уравнения (2.3) относительно приближенного решения (2.14)
![]() .
.
Будем искать, в
соответствии с рекомендацией метода
Галеркина, коэффициенты
![]() из
условий ортогональности
из
условий ортогональности
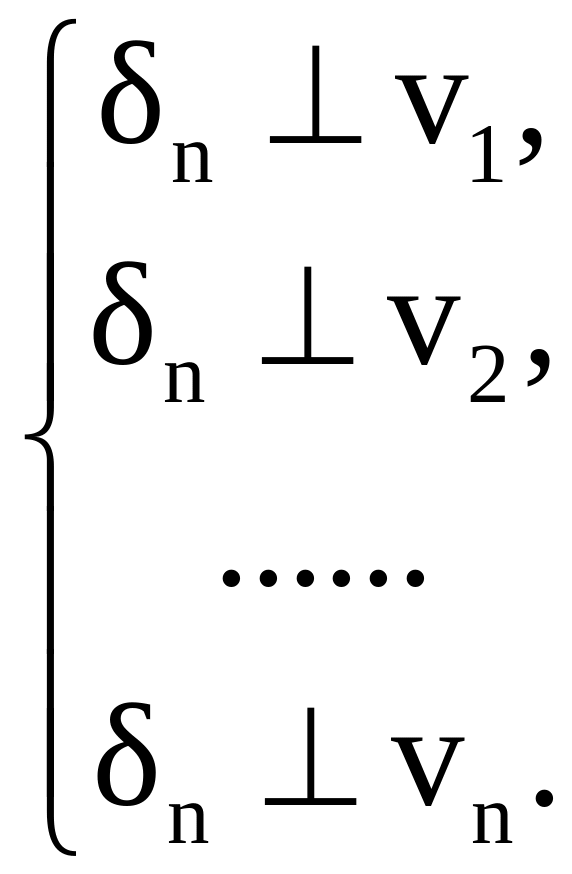 (2.15)
(2.15)
Условия (2.15)
означают, что проекция невязки на
плоскость, натянутую на координатные
векторы
![]() ,
равна нулю.
,
равна нулю.
Из определения
ортогональности и свойств скалярного
произведения легко получить, что условия
(2.15) эквивалентны системе уравнений
(2.8) с коэффициентами
![]() и правыми частями
и правыми частями
![]() ,
вычисляемыми по формулам (2.9) и
(2.10).Система (2.8), полученная из условий
(2.15), называется галеркинским
приближением
краевой
задачи (2.1).
Решая эту систему и подставляя результат
вычислений в (2.14), получим приближенное
решение краевой задачи.
,
вычисляемыми по формулам (2.9) и
(2.10).Система (2.8), полученная из условий
(2.15), называется галеркинским
приближением
краевой
задачи (2.1).
Решая эту систему и подставляя результат
вычислений в (2.14), получим приближенное
решение краевой задачи.
Пример 8. Пусть
в (2.1) область
ограничена эллипсом
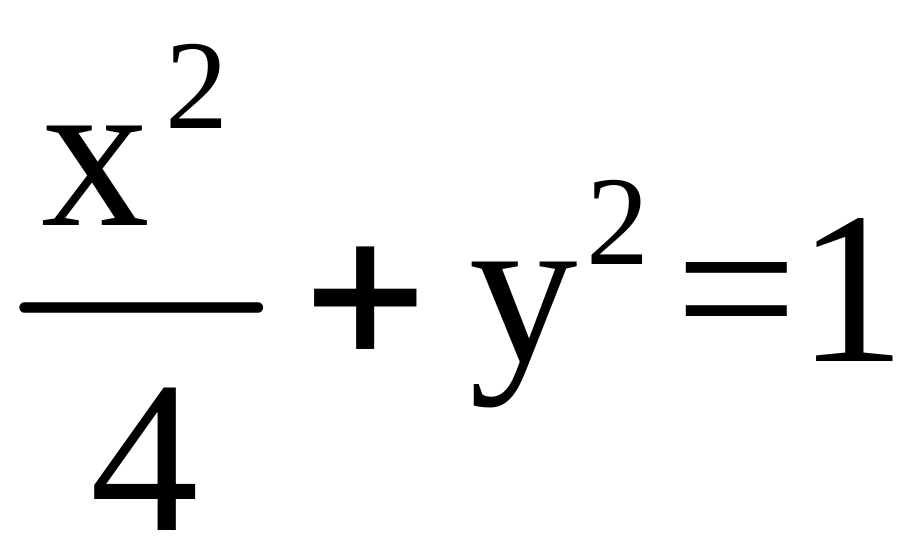 и осями координат (рис. 7),
и осями координат (рис. 7),
![]() .
.
Рис. 7 |
|
Решение. В
качестве координатной системы возьмем
последовательность функций
![]() ,
где
,
где
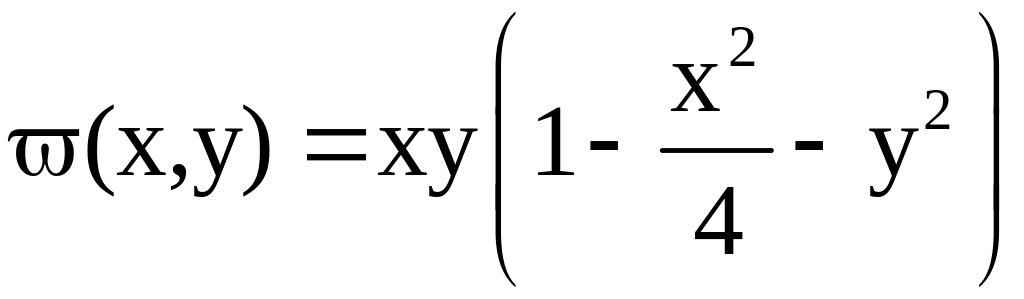 .
.
Заметим, что
![]() удовлетворяет условиям 1) – 3) пункта 2
предыдущего параграфа.
удовлетворяет условиям 1) – 3) пункта 2
предыдущего параграфа.
В выражении (2.14) ограничимся тремя членами; обозначая
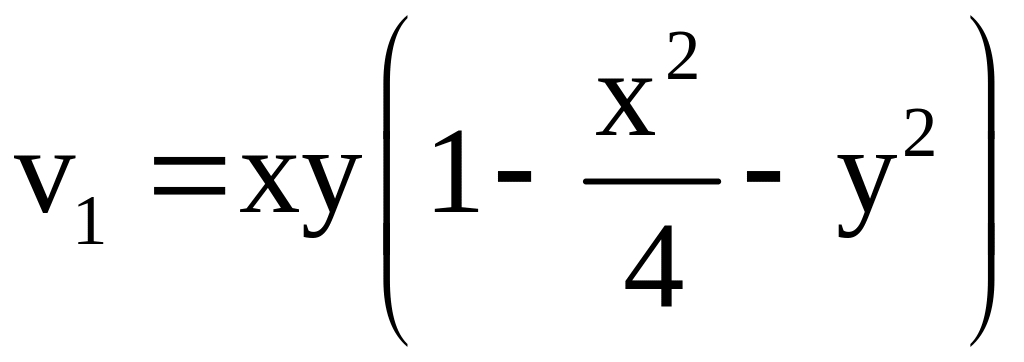 ,
,
 ,
,
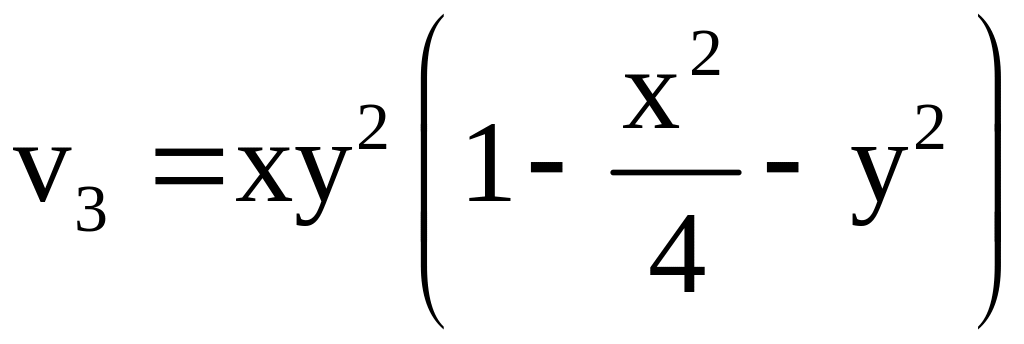 ,
,
будем иметь
![]() .
.
Составим невязку
![]() ;
;
наложим на нее требование ортогональности
![]() ,
,
![]() ,
,
![]() ;
;
вычислим коэффициенты и правые части полученной из этих условий системы по формулам (2.9) и (2.10). Например,
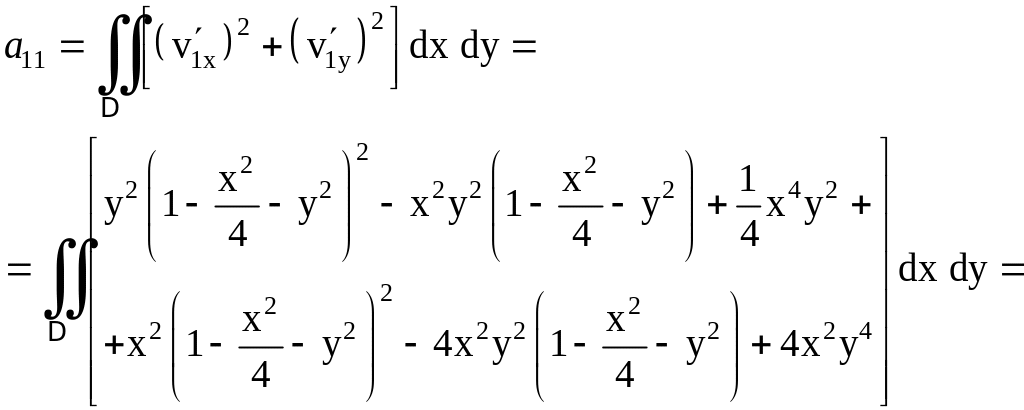
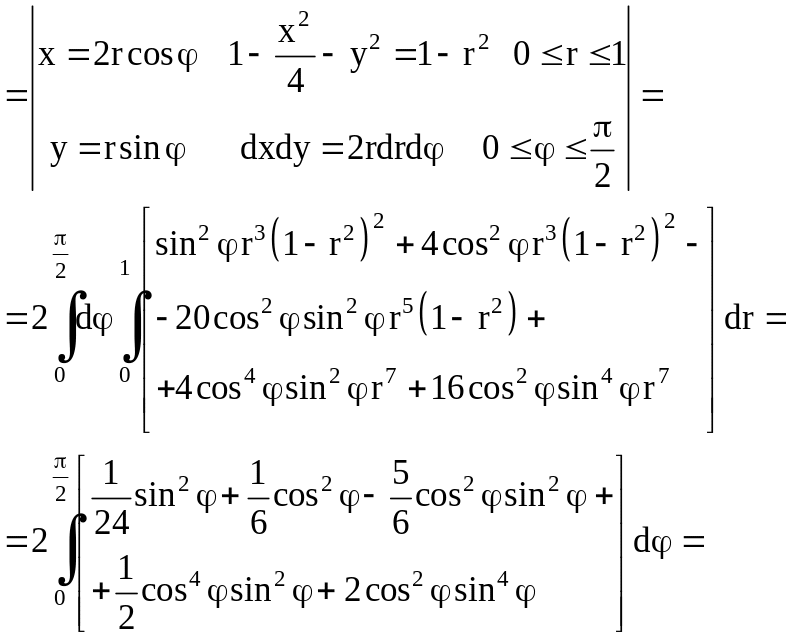

Аналогично можно получить
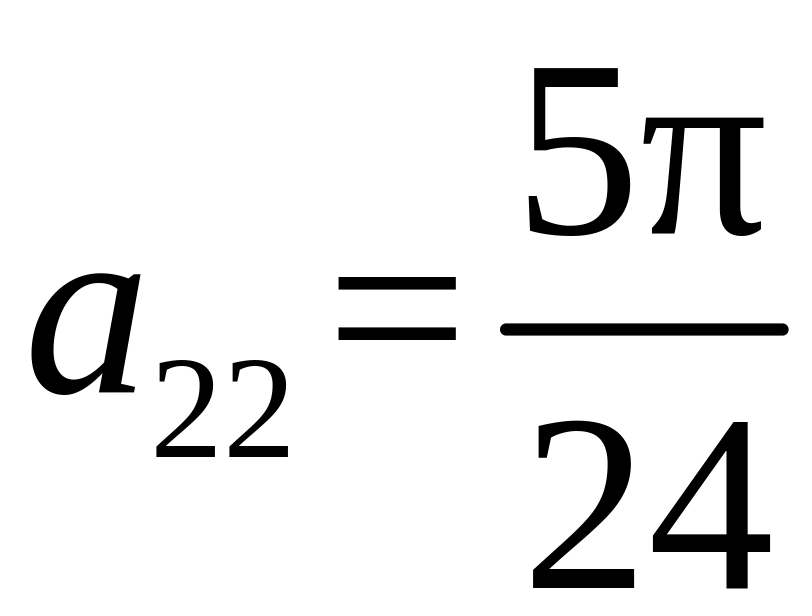 ;
;
 ;
;
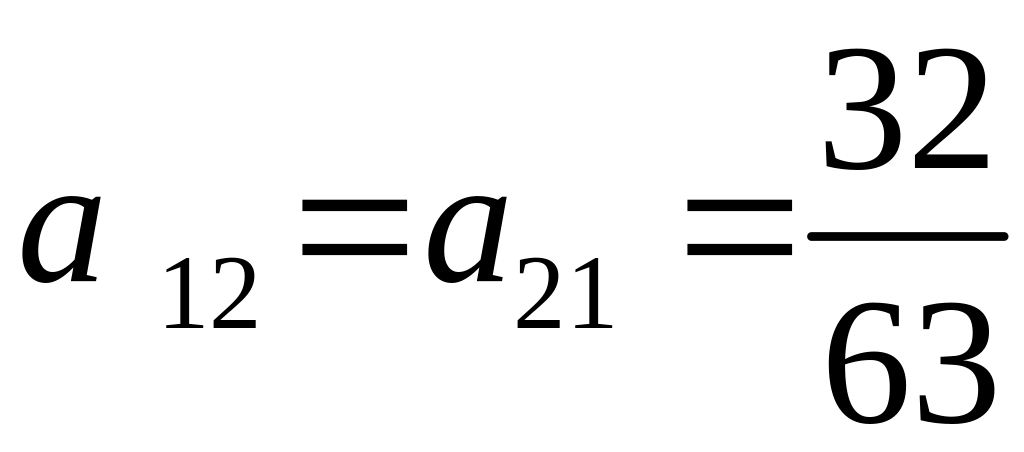 ;
;
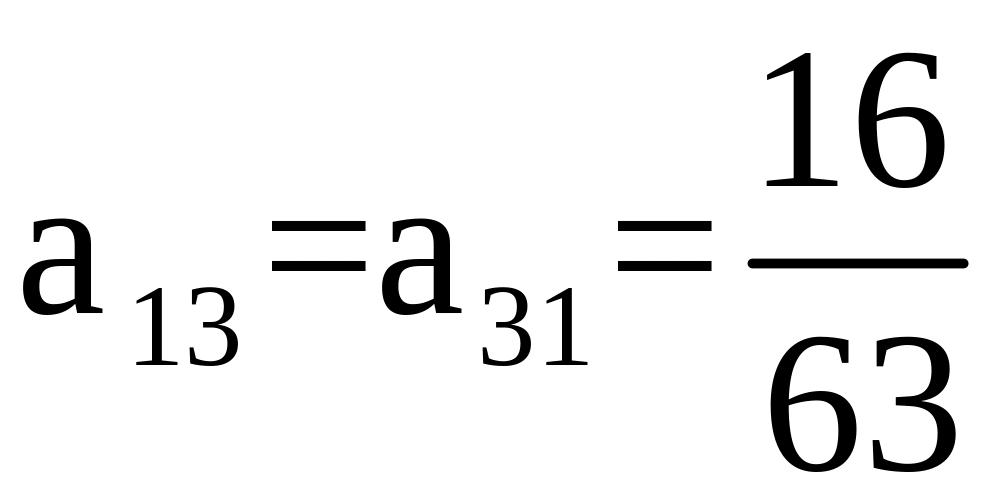 ;
;
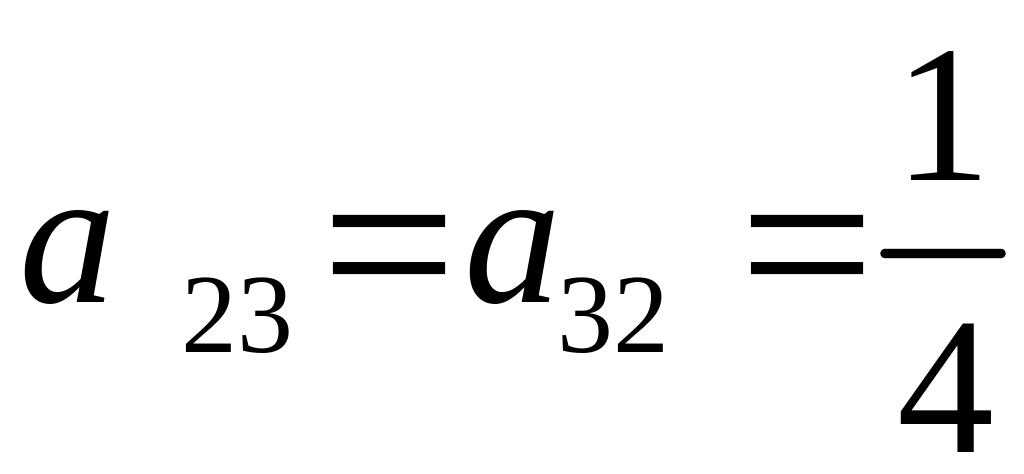 ;
;
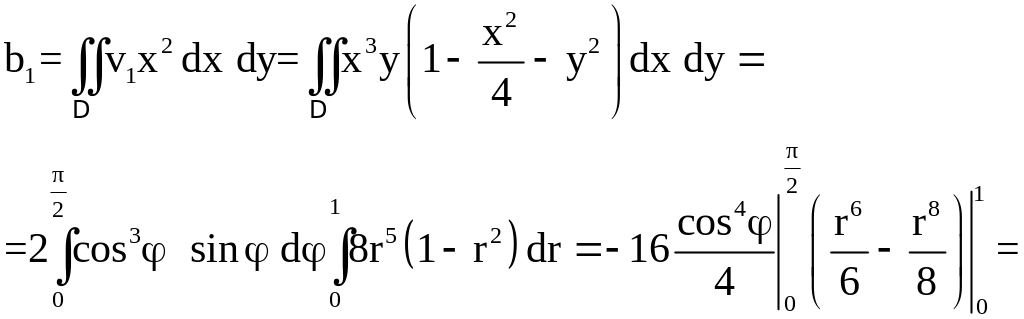
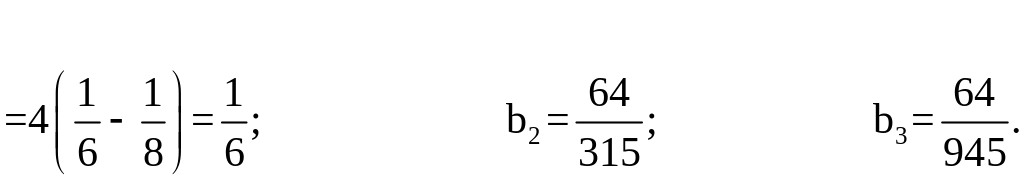
Построим систему
уравнений для
![]() ,
т.е. галеркинское приближение краевой
задачи (2.16),
,
т.е. галеркинское приближение краевой
задачи (2.16),
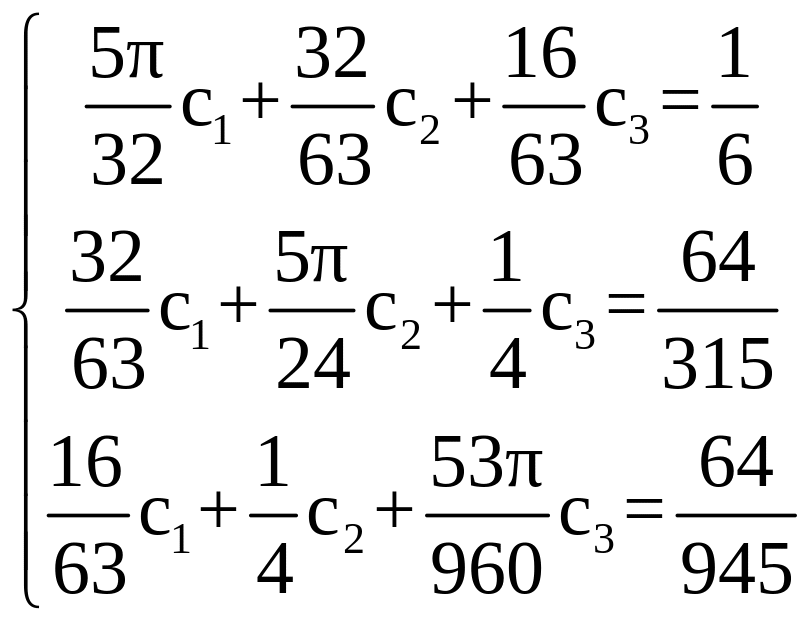 ,
,
решая которую, получим
![]() ,
,
![]() ,
,
![]() ,
,
поэтому искомая функция
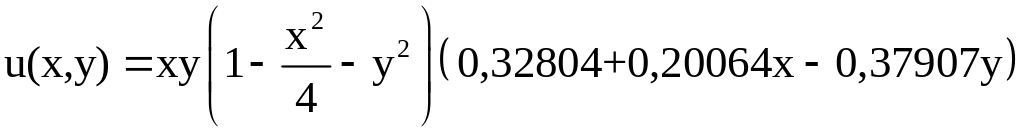 .
.
Типовой расчет
Найти решение задачи Дирихле для уравнения Пуассона
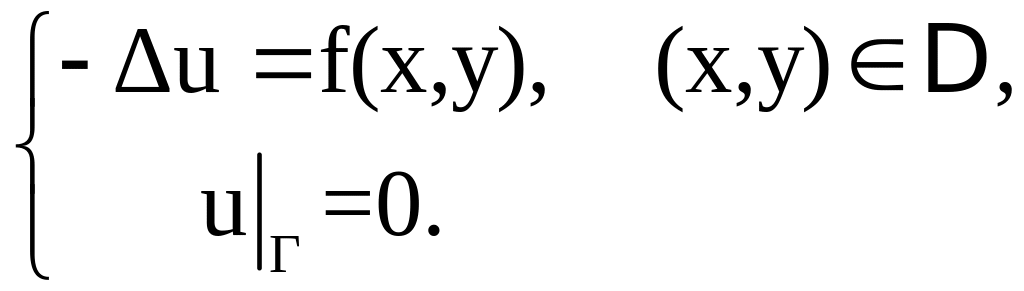
Метод решения задачи указывается преподавателем.
 ;
:
треугольник со сторонами
;
:
треугольник со сторонами
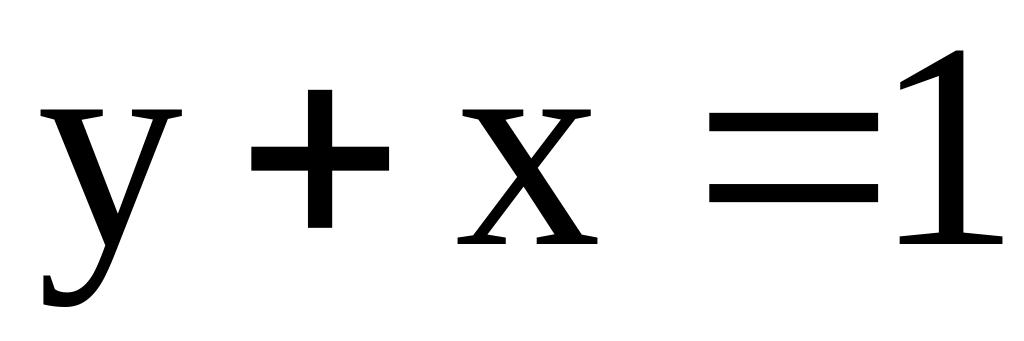 ,
,
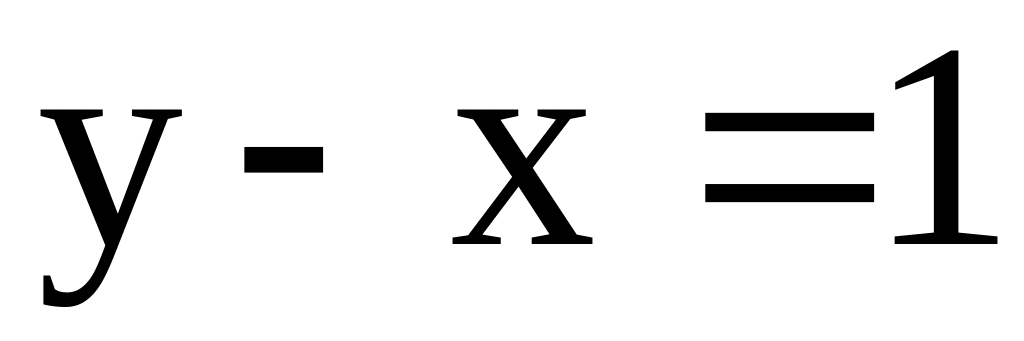 ,
;
,
;
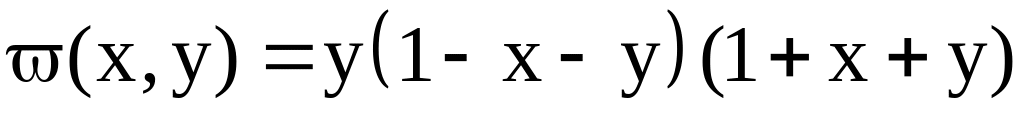 .
.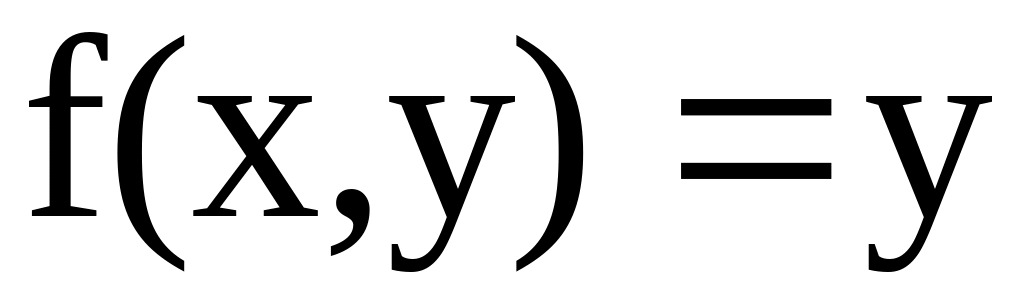 ;
:
треугольник со сторонами
,
,
;
:
треугольник со сторонами
,
,
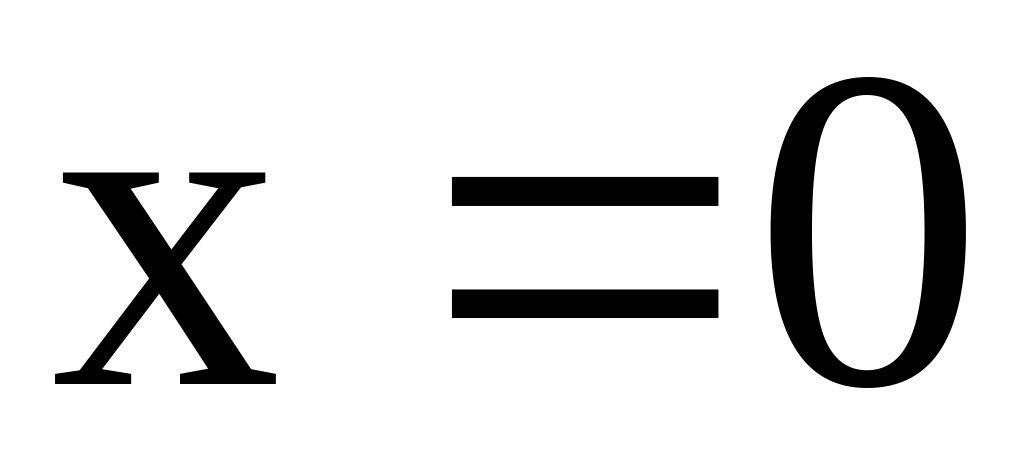 ;
;
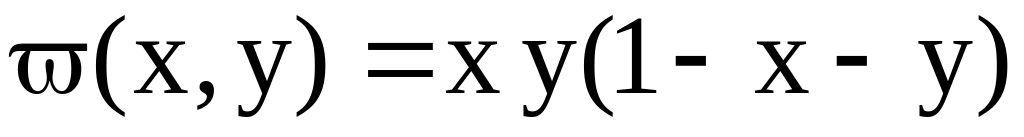 .
.; : прямоугольник
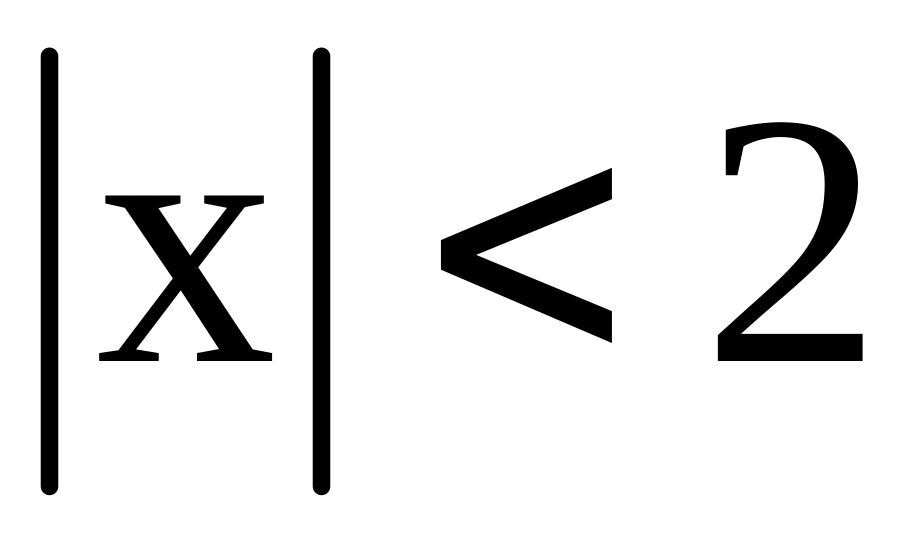 ,
,
 ;
;
![]() .
.
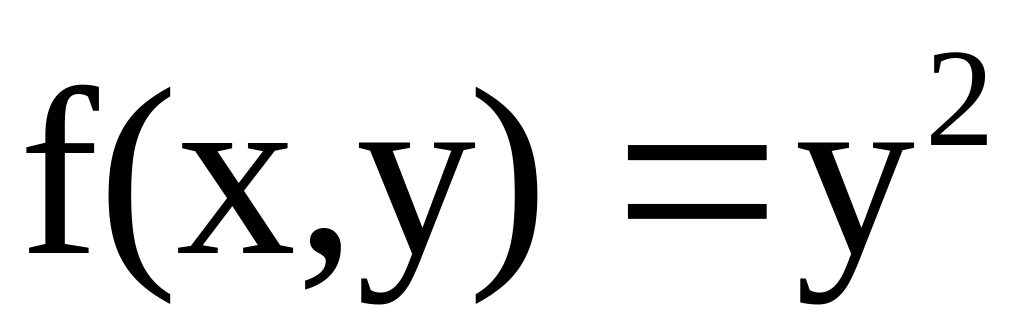 ;
:
прямоугольник
;
:
прямоугольник
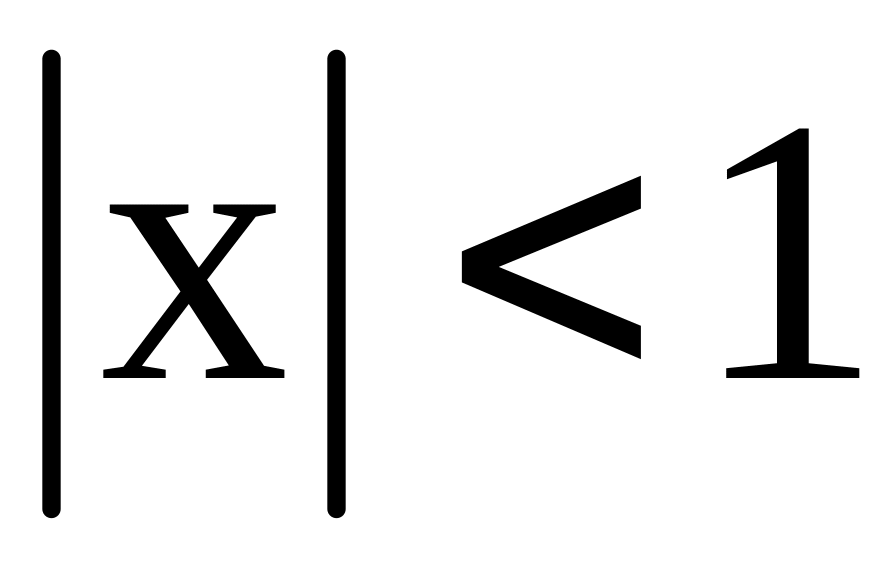 ,
,
 ;
;
![]() .
.
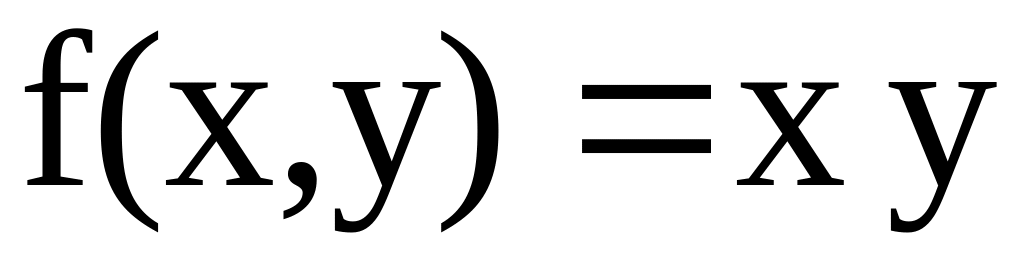 ;
:
прямоугольник
;
:
прямоугольник
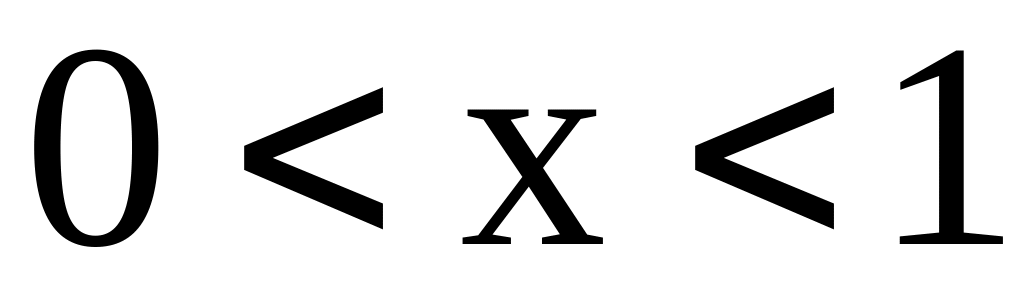 ,
;
,
;
![]() .
.
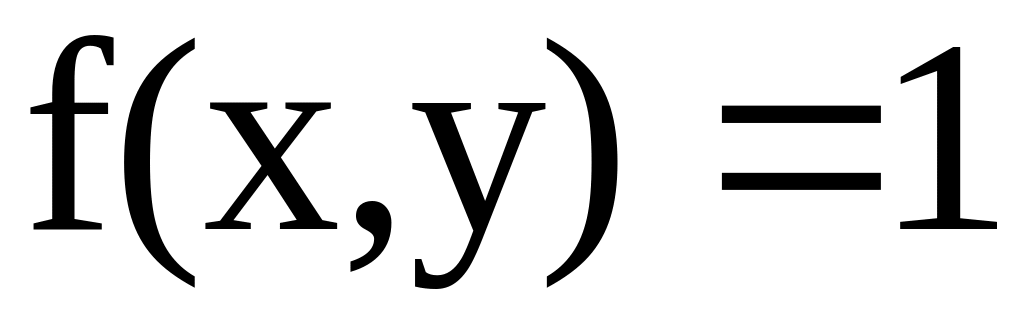 ;
:
прямоугольник
;
:
прямоугольник
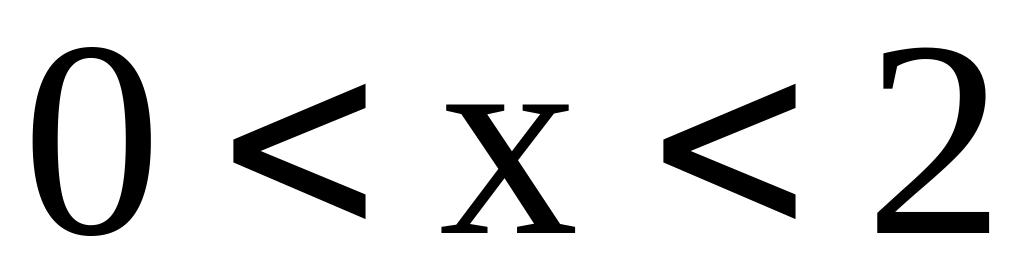 ,
,
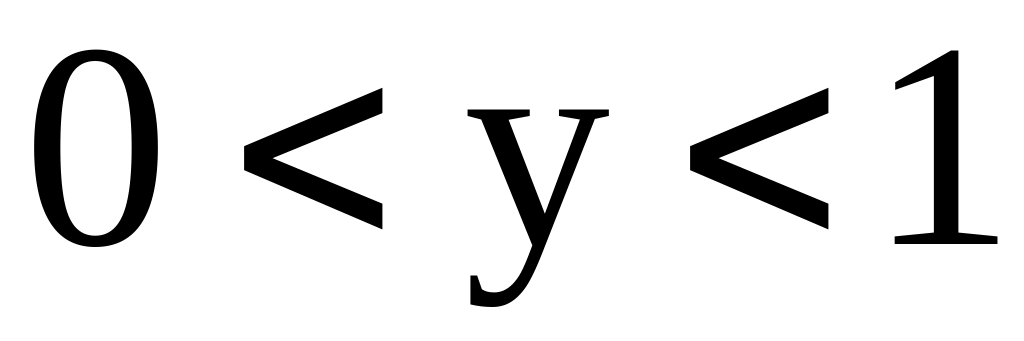 ;
;
![]() .
.
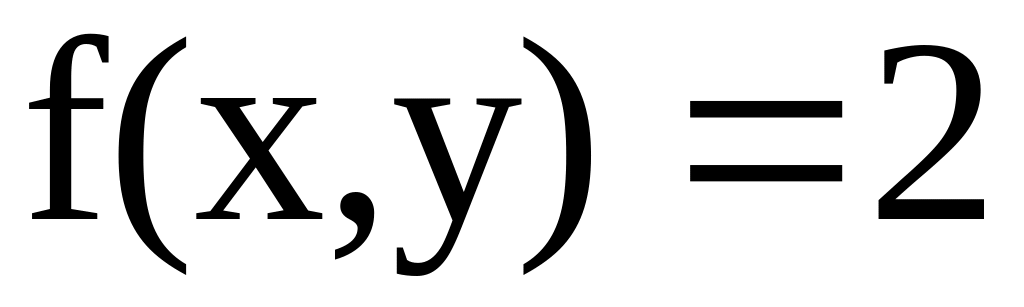 ;
:
квадрат
,
;
:
квадрат
,
 ;
;
![]() .
.
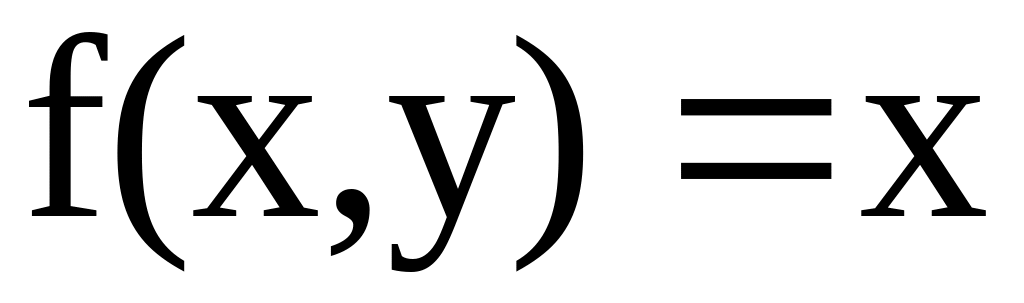 ;
:
область, ограниченная параболой
;
:
область, ограниченная параболой
 и осью
и осью
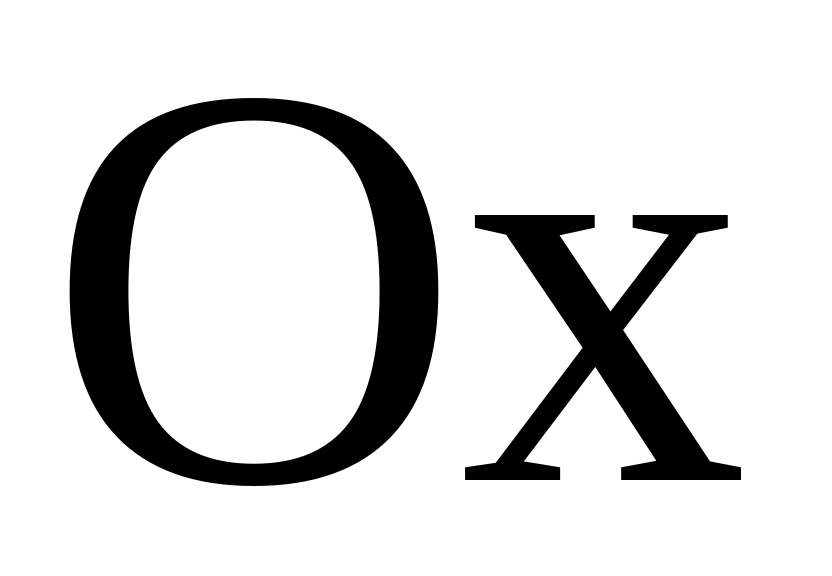 ;
;
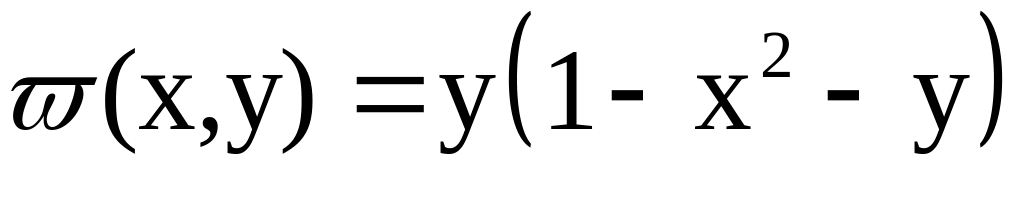 .
.; : область, ограниченная параболой и осями координат
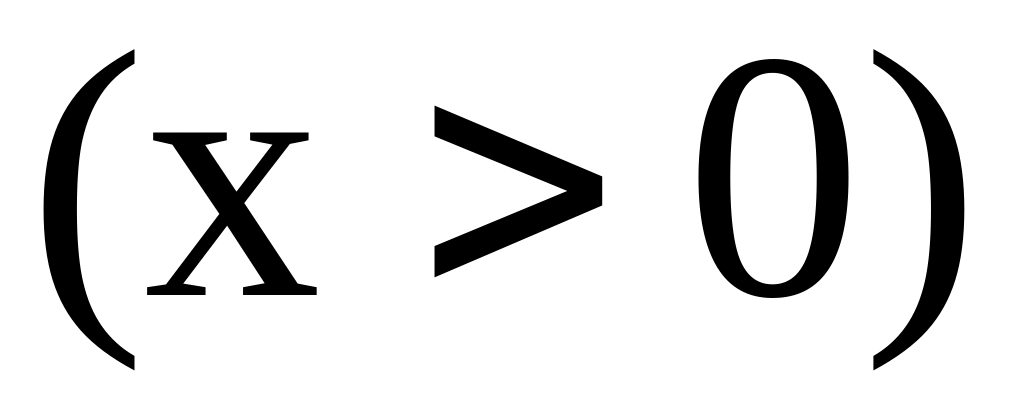 ;
.
;
.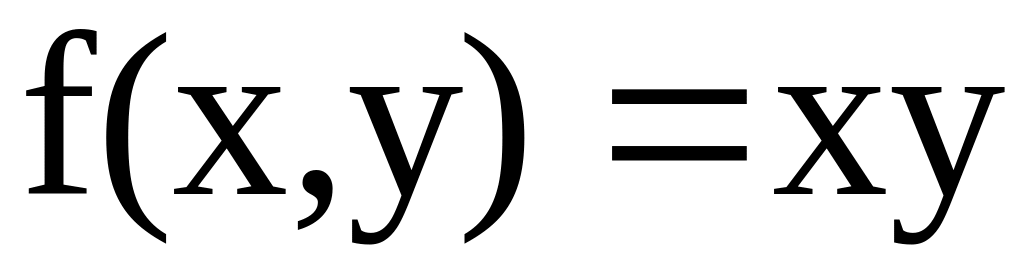 ;
:
внутренность эллипса
;
:
внутренность эллипса
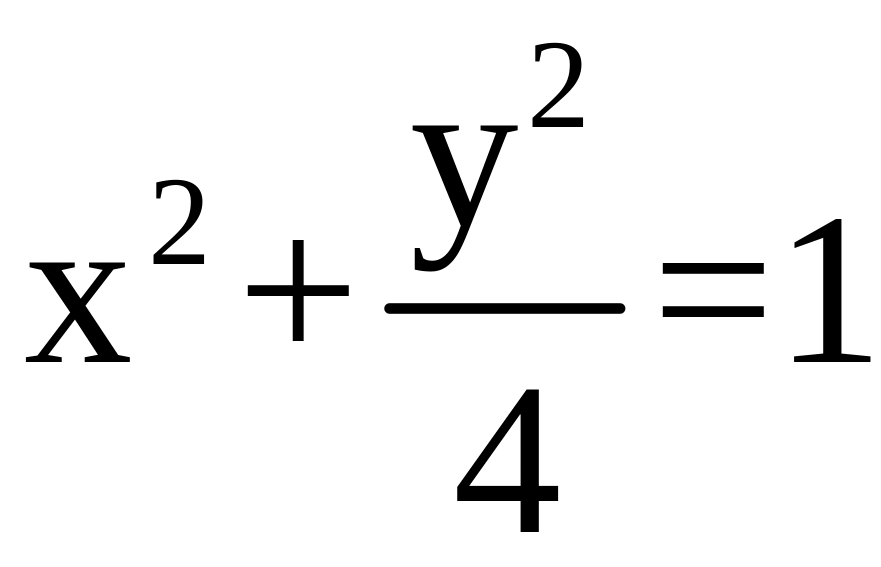 ;
;
 .
.
; : область, ограниченная эллипсом
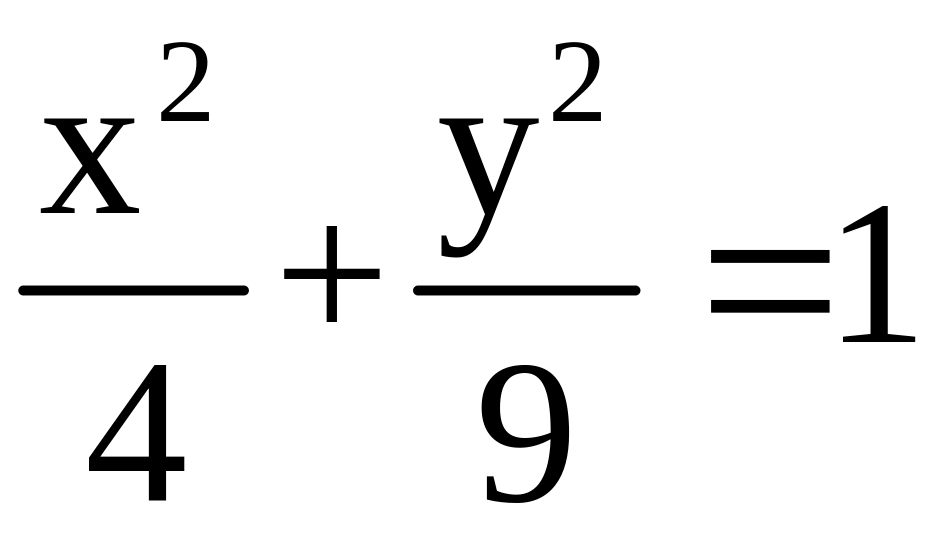 и осью
и осью
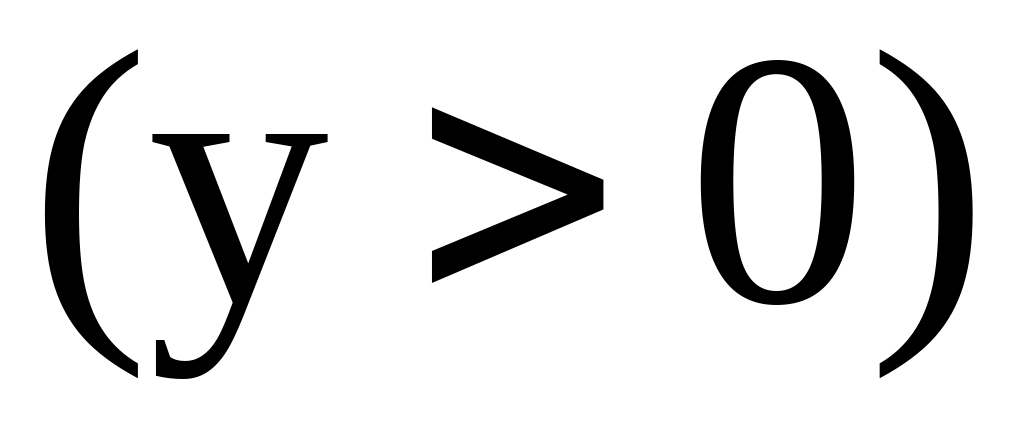 ;
;
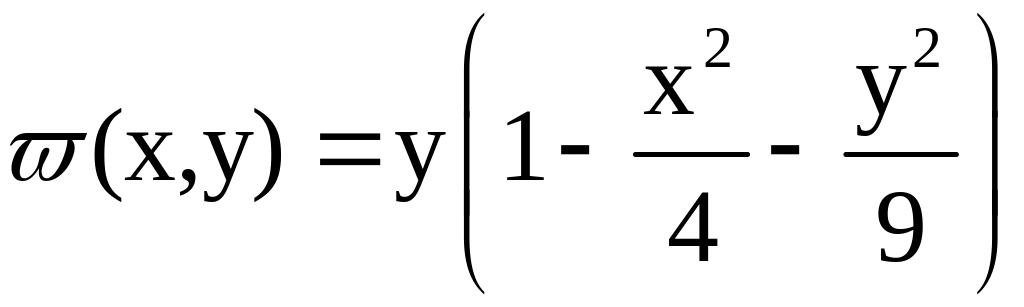 .
.; : круг
 ;
;
![]() .
.
 ;
:
полукруг
;
:
полукруг
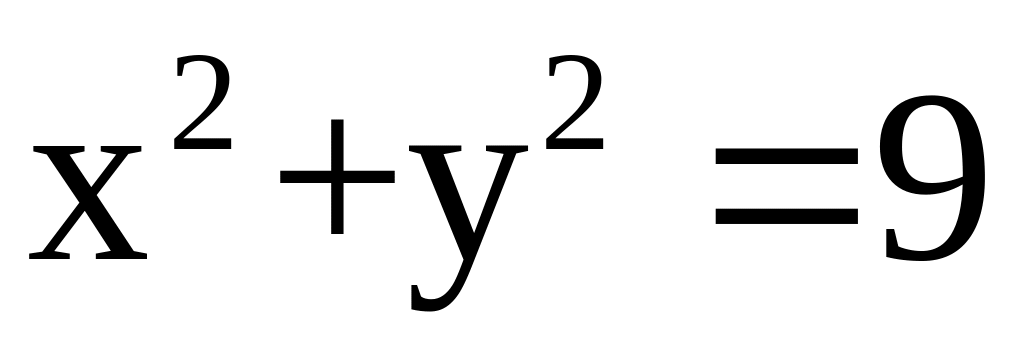 ,
,
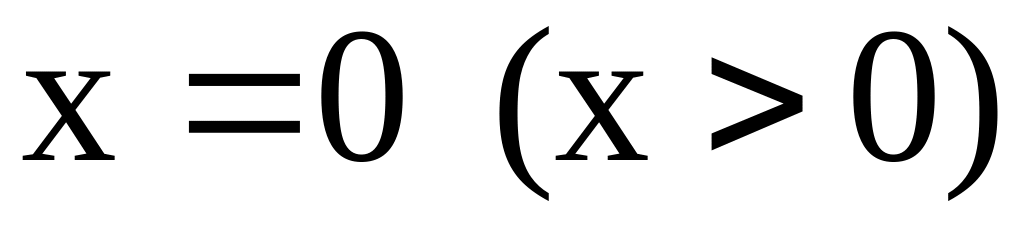 ;
;
![]() .
.


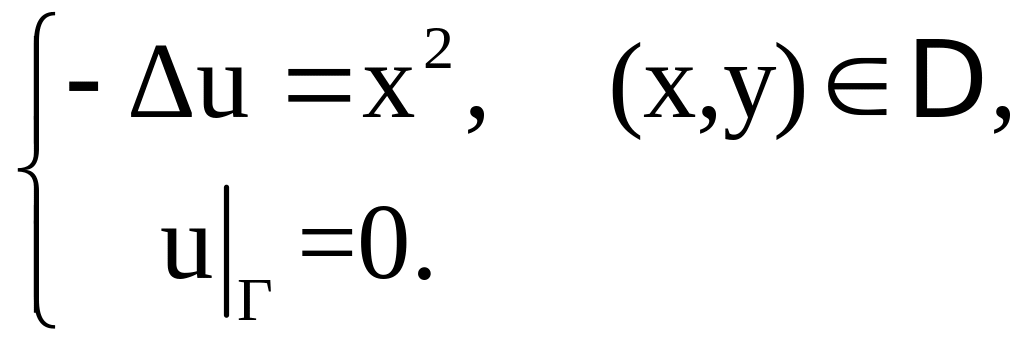 (2.16)
(2.16)