Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Орский гуманитарно-технологический институт (филиал ОГУ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЗакКонКПер с круговыми зубьями_1201,1502_в.doc

Скачиваний:

Добавлен:

01.04.2025

Размер:

1.36 Mб

Скачать

☆

Министерство образования Российской Федерации

Орский гуманитарно-технологический институт (филиал)

Государственного образовательного учреждения высшего профессионального образования «Оренбургский государственный университет»

кафедра общепрофессиональных дисциплин

Методические указания по расчету закрытых конических передач с круговыми зубьями

для студентов специальностей 1201, 1502

г.Орск—2003г

ББК-34.44

Б 332

УДК 621.81

Методика расчета зубчатых передач по дисциплинам «Детали машин и основы конструирования машин», «Детали машин» для студентов специальностей 1201, 1502

Составители: Г.С. Баширова, Е.В. Баширова, Д.В. Анненков

 Издательство Орского Гуманитарно-Технологического Института, 2003

1 Методика расчета конических передач с круговыми зубьями

Введение

Зубчатая передача является механизмом, который с помощью зубчатого зацепления передает или преобразует движение с изменением угловых скоростей или моментов.

Конические колеса применяют для передачи движения между валами, оси которых пересекаются. Угол между осями колес  (межосевой угол =₁+₂, ₁ – угол делительного конуса шестерни; ₂ – угол делительного конуса колеса) теоретически может быть любым в диапазоне 10⁰<<170⁰. Наибольшее распространение получили ортогональные передачи с углом =90⁰ (рис.1). По расположению зубьев на колесе конические передачи бывают прямозубые (рис.1а), косозубые (рис.1б) и с круговыми зубьями (рис.1в).

а) б) в)

Рис.1. Передачи конические

Конические колеса значительно сложнее в изготовлении и монтаже. Помимо допусков на размеры зубьев и углы делительных конусов при сборке необходимо достигнуть совпадение вершин конусов шестерни и колеса.

1.1 Выбор материала колеса, термообработки и твердости

Материал зубчатых колес должен обеспечить:

стойкость поверхностных слоев зуба против усталостного выкрашивания и абразивного износа;
прочность зуба на изгиб;
соответствие технологических свойств материала намечаемому способу обработки;
минимальные значения веса и размеров колес;
минимальную стоимость.

Стальные зубчатые колеса

Стальные зубчатые колеса с твердостью 350HB из углеродистых сталей и легированных сталей с отжигом, нормализацией и улучшением рекомендуется применять:

в мелкосерийном производстве;
в мало- и средненагруженных передачах;
в передачах подвергаемых большим динамическим и ударным нагрузкам;
в передачах с колесами больших диаметров (термическая обработка которых затруднена).

Колеса малых и средних диаметров выполняются из поковок или проката.

Колеса диаметров >500мм рекомендуется изготавливать из стального литья (35Л, 40Л, 50Л), применяя их в паре с кованной шестерней при окружной скорости V<8м/с.

Стальные зубчатые колеса с твердостью >350HB из углеродистых и легированных сталей с дополнительной термической обработкой поверхности зуба после нарезания рекомендуется применять:

в массовом и крупносерийном производстве;
в высоконагруженных передачах;
в передачах, габариты которых ограничены специальными требованиями;
при отсутствии требований, ограничивающих стоимость.

При использовании зубчатых колес с >350HB рекомендуется применять повышенную точность изготовления колес, увеличивать жесткость валов.

Зубчатые колеса из чугуна

Серый чугун рекомендуется применять для:

тихоходных, преимущественно крупных открытых передач, габариты которых не ограничены какими-либо требованиями;
редко работающих, сменных колес.

Модифицированный и высокопрочный чугун рекомендуется применять при окружных скоростях V<6м/с взамен стального литья для снижения стоимости.

Неметаллические колеса

Неметаллические материалы можно рекомендовать для изготовления зубчатых колес:

в малонагруженных передачах;
в силовых высокоскоростных передачах в паре с металлическими колесами для уменьшения шума.

Стальные колеса, работающие в паре с неметаллическими должны иметь твердость >250HB; ширина металлических колес принимается несколько больше, чем у неметаллических.

Материал открытых зубчатых передач

Открытые передачи чаще всего выполняются прямозубыми и работают с небольшими скоростями, как правило менее 1м/с. Такие передачи прирабатываются при всех твердостях, но изготавливают их в большинстве случаев из нормализованных или улучшенных сталей.

1.2 Выбор твердости рабочей поверхности зуба

1.2.1 Прямозубые колеса

Для прямозубых колес с твердостью <НВ350 рекомендуется соблюдать следующие соотношения твердости колеса и шестерни:

НВ_шест.-НВ_кол.=20…50

Это достигается:

выбором разных материалов для изготовления шестерни и колеса,

например: шестерня – сталь 45, НВ250;

колесо – сталь 50, НВ200.

выбором одной и той же марки стали для шестерни и колеса с различной термической обработкой,

например: шестерни – сталь 40Х, улучшенная НВ270;

колесо – сталь 40Х, нормализованная НВ 230.

При высокой твердости рабочих поверхностей с твердостью >НВ350 рекомендуется обеспечить одинаковую твердость для шестерни и колеса:

НВ_шест.НВ_кол.

1.2.3 Косозубые колеса и колеса с круговые зубьями

В передачах с косыми и круговыми зубьями рекомендуется соблюдать следующие соотношения твердости колеса и шестерни:

НВ_шест.-НВ_кол.=80…250

Например, шестерня – сталь 40Х, улучшенная НВ270 с дополнительной закалкой ТВЧ до НВ500; колесо – сталь 40Х, улучшенная НВ240 или шестерня – сталь 50Г, улучшенная НВ240; колесо – сталь 40, нормализованная НВ150.

В двух- трех- четырехступенчатых редукторах (для сокращения номенклатуры материалов) рекомендуется назначать:

одну марку материала для всех шестерен и другую марку материала для всех колес;
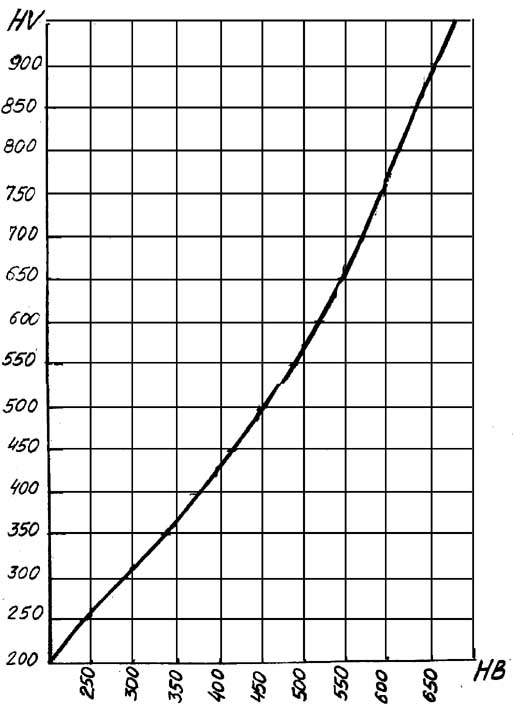
одну и ту же марку материала для всех колес и шестерен.

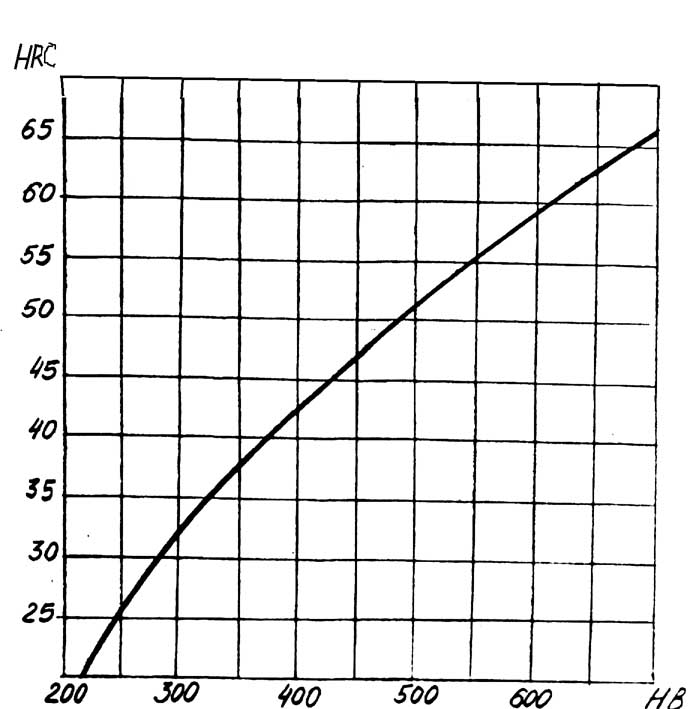
Рис.2. График соотношения твердостей, выраженных в единицах HB и HV

Рис.3. График соотношения твердостей, выраженных в единицах HB и HRC

Рекомендуемый выбор материала, термообработки, твердости и механических свойств сталей приводится в таблице 1.

Таблица 1

Механические свойства стали

Марка стали	Диаметр, D, мм	Ширина, мм	НВ сердцевины	HRC поверхности	_В	_Т	Вид термообработки
Марка стали	Диаметр, D, мм	Ширина, мм	НВ сердцевины	HRC поверхности	МПа		Вид термообработки
35	любой	любая	163-192	-	550	270	Нормализация
45	любой	любая	179-207	-	600	320	Нормализация
45	125	80	235-262	-	780	540	Улучшение
45	80	50	269-302	-	890	650	Улучшение
40Х	200	125	235-262	-	790	640	Улучшение
40Х	125	80	269-302	-	900	750	Улучшение
40Х	125	80	269-302	45-50	900	750	улучшение + закалка ТВЧ
35ХМ	315	200	235-262	-	800	670	Улучшение
35ХМ	200	125	269-302	-	920	790	Улучшение
35ХМ	200	125	269-302	48-53	920	790	улучшение + закалка ТВЧ
40ХН	315	200	235-262	-	800	630	Улучшение
40ХН	200	125	269-302	-	920	750	Улучшение
40ХН	200	125	269-302	48-53	920	750	улучшение + закалка ТВЧ
20ХН2М	200	125	300-400	56-63	1000	800	улучшение + цементация + закалка
18ХГТ	200	125	300-400	56-63	1000	800	улучшение + цементация + закалка
12Н3А	200	125	300-400	56-63	1000	800	улучшение + цементация + закалка
25ХГМ	200	125	300-400	56-63	1000	800	улучшение + цементация + закалка
40ХН2МА	125	80	269-302	40-56	980	780	улучшение + азотирование
35Л	любой	любая	163-207	-	550	270	Нормализация
45Л	315	200	207-235	-	680	440	Улучшение
40Л	315	200	235-262	-	850	600	Улучшение

1.3 Допускаемые контактные напряжения

где _H_limb– предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов перемены напряжений, МПа (табл.2);

Таблица 2

Значения Hlimb и Flimb

Способы ТО и ХТО зубьев	Средняя твердость поверхности зубьев	Стали	_Hlimb, МПа	_Flimb, МПа
Отжиг, нормализация или улучшение	Н<НВ350	Стали углеродистые и легированные	_Hlimb=2НВ+70	_Flimb=1,8HB
Объемная закалка	HRC45…55		_Hlimb=18НRC+150	_Flimb=500
Поверхностная закалка	HRC42…50		_Hlimb=17НRC+200	_Flimb=17HRC_пов+200
Цементация и нитроцементация	Н>HRC56	Стали легированные	_Hlimb=23НRC	_Flimb=600…750
Азотирование	HV550…750	Стали легированные	_Hlimb=1050	_Flimb=10HRC_серд+240

S_H – коэффициент запаса прочности:

для колес с однородной структурой материала: S_H=1,1;

для колес с поверхностным упрочнением: S_H=1,2;

Z_R– коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев; принимают в зависимости от параметра шероховатости;

для Ra=1,25…0,63 Z_R=1,0

для Ra=2,5…1,25 Z_R=0,95

для Rz=40…10 Z_R=0,90

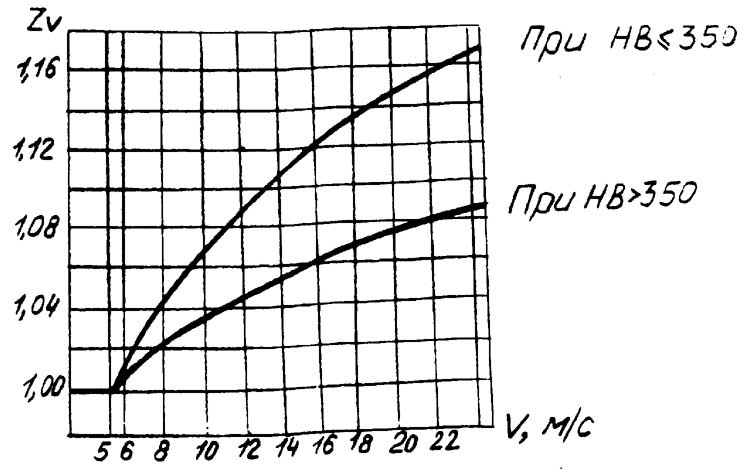
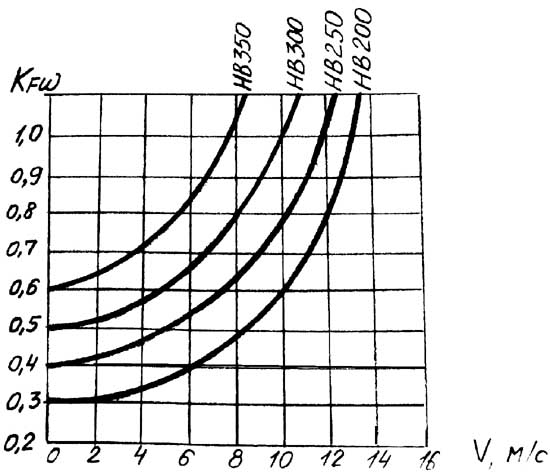
Z_V– коэффициент, учитывающий окружную скорость; определяют по рис.4 в зависимости от твердости рабочих поверхностей зубьев и окружной скорости V в зацеплении или определить по формуле:

при твердости 350НВ Z_V=0,85_*V^0,1

при твердости >350НВ Z_V=0,925_*V^0,05

Рис.4. График для определения Z_V

При проектном расчете, когда размеры зубчатых колес еще не известны, для приближенного определения окружной скорости можно воспользоваться зависимостью:

где n₁ – частота вращения шестерни, об/мин;

u – передаточное число;

Т₂ – вращающий момент на валу колеса, Нм;

С_V – вспомогательный коэффициент, табл.3;

_ba – коэффициент ширины колеса, табл.4.

Таблица 3

Значение коэффициента сv

Передача	Обработка
Передача	У₁+У₂	ТВЧ₁+У₂	Ц₁+У₂	ТВЧ₁+ТВЧ₂ З₁+З₂	Ц₁+Ц₂
Коническая с круговыми зубьями	10	10	11	11	13,5
Примечание. У – улучшение; З – закалка объемная; ТВЧ – закалка поверхности при нагреве ТВЧ; Ц – цементация

Таблица 4

Значение коэффициента ba

При расположении зубчатых колес относительно опор
Симметричное	Несимметричное	Консольное (одно или обоих зубчатых колес)
0,315…0,50	0,25…0,40	0,20…0,25
Для шевронных передач: _ba=0,40…0,63 Стандартный ряд _ba: 0,20; 0,25; 0,315; 0,40; 0,50.

Z_L– коэффициент, учитывающий влияние смазки;

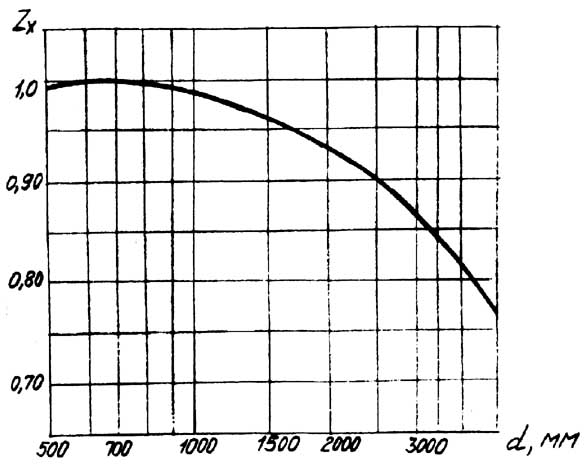
Z_X– коэффициент, учитывающий размер зубчатого колеса; определяют по рис.5 или по формуле:

где d – делительный диаметр, мм;

при d<1000мм Z_X=1.

Рис.5. График для определения Z_X

При расчете допускаемых контактных напряжений следует принимать Z_R_*Z_V_*Z_L_*Z_X=0,9.

Z_N– коэффициент долговечности; определяется по рис.7 или по формуле:

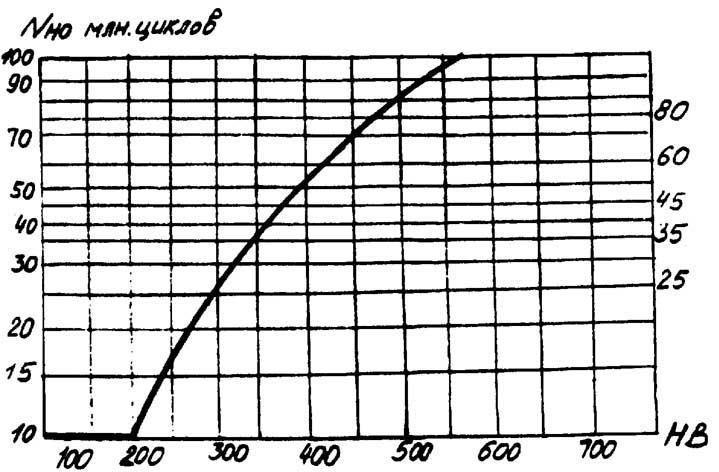
где N_HO – базовое число циклов перемены напряжений, соответствующее пределу выносливости, млн циклов; определяется по рис.6 или по формуле:

N_HO=30_*HB_cp^2,4

Рис.6. График для определения N_HO

N_HE- эквивалентное число циклов перемены напряжений за весь срок службы (наработка), млн. циклов.

m_H – показатель корня;

При постоянной нагрузке:

N_HE=60_*c_*n_i*t_,

здесь с – число одинаковых колес, сцепляющихся с рассчитываемым;

n_i – частота вращения рассчитываемого колеса;

t_– срок службы привода (ресурс), ч;

t_=365_*k_г_*24_*k_c*L,

здесь k_г, k_c – коэффициент использования передачи в течении года, суток;

L – срок службы привода, лет.

При переменном режиме работы:

здесь Т_i – один из крутящих моментов согласно графика нагрузки;

Т_max – максимально длительно действующий из моментов;

n_i, t_i – соответствующие этим моментам (Т_i) частота вращения и время работы.

При N_HEN_HO коэффициент долговечности Z_N определяется по рис.6 или по формуле:

При однородной структуре материала (нормализация, улучшение, объемная закалка) Z_N2,6.

При поверхностном упрочнении Z_N1,8.

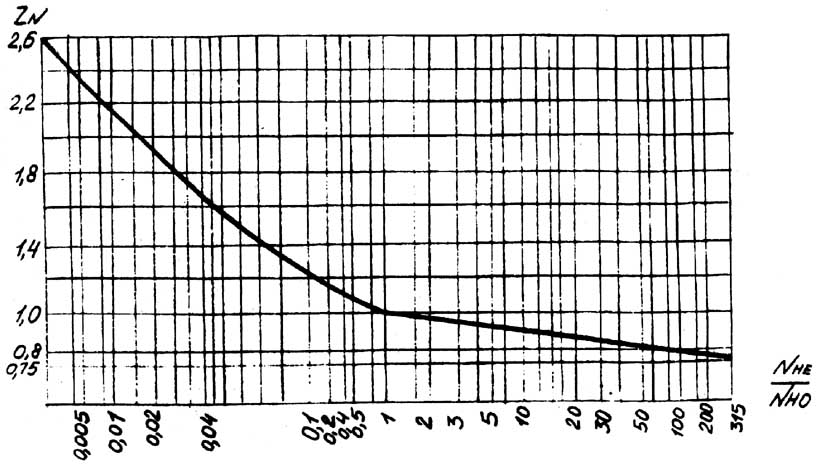
При N_HE>N_HO коэффициент долговечности Z_N определяется по рис.6 или по формуле:

принимая Z_N не менее 0,75.

Рис.7. График для определения Z_N

Допускаемое контактное напряжение следует определить для зубьев шестерни []_H1 и колеса []_H2.

Для зубчатых передач с непрямыми зубьями в качестве расчетного допускаемого контактного напряжения принимают:

[]_H=0,45_*([]_H1+[]_H2)1,15_*[]_H2

1.4 Допускаемые напряжения изгиба

где _Flimb– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений, МПа (см.табл.2);

S_F – коэффициент запаса прочности:

S_F=1,7…2,2 (большие значения для литых заготовок);

Y_R – коэффициент, учитывающий влияние шероховатости поверхности;

Y_R=1 – для шлифования и зубофрезерования при шероховатости не более Rz=40мкм;

Y_R=1,05 – для полирования при цементации, нитроцементации, азотировании (полирование до ХТО);

Y_R=1,2 – для полирования при нормализации и улучшении;

Y_C– коэффициент, учитывающий двухстороннее приложение нагрузки безопасности;

Y_С=1 – при одностороннем приложении нагрузки;

Y_С=0,7…0,8 – при реверсивной нагрузке;

Y_N– коэффициент долговечности, определяется по формуле:

здесь N_FO – базовое число циклов перемены напряжений, соответствующее пределу выносливости, N_FO=4_*10⁶для всех сталей;

N_FE- эквивалентное число циклов перемены напряжений за весь срок службы (наработка).

При постоянной нагрузке:

N_FE=60_*c_*n_i*t_,

здесь с – число одинаковых колес, сцепляющихся с рассчитываемым;

n_i – частота вращения рассчитываемого колеса;

t_– срок службы привода (ресурс), ч;

t_=365_*k_г_*24_*k_c*L,

здесь k_г, k_c – коэффициент использования передачи в течении года, суток;

L – срок службы привода, лет.

При переменном режиме работы:

здесь Т_i – один из крутящих моментов согласно графика нагрузки;

Т_max – максимально длительно действующий из моментов;

n_i, t_i – соответствующие этим моментам (Т_i) частота вращения и время работы.

m_F – показатель корня;

m_F=6 – при твердости поверхности зубьев 350НВ;

m_F=9 – при твердости поверхности зубьев >350НВ;

При N_F_EN_F_O коэффициент долговечности Y_N=1;

Если N_F_E<N_F_O коэффициент долговечности Y_Nmax=4 при m_F=6;

Y_Nmax=2,5 при m_F=9.

1.5 Проектный расчет закрытой конической передачи с круговыми зубьями

1.5.1 Внешний делительный диаметр колеса

где Т₂ – вращающий момент на валу колеса, Н_*м;

u – передаточное число рассчитываемой передачи;

k'_HB – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (предварительный) (см.рис.10);

k'_HB=1 для прирабатывающихся колес с прямыми зубьями;

_bR=b/R_e0,3 – коэффициент относительной ширины колес; при проектном расчете передачи рекомендуется принимать _bR=0,285.

[]_H – расчетное допускаемое контактное напряжение, МПа;

_Н– коэффициент, учитывающий вид конической передачи;

_Н=0,8+0,15_*u – для конических колес с высокой поверхностной твердостью;

_Н=1,2+0,2_*u – для конических колес при твердость менее 350НВ.

Расчетное значение d_e2 округлить до ближайшего стандартного значения (табл.5).

Таблица 5

Диаметры внешних делительных окружностей

Ряд 1	50	63	80	100	125	160	200	250	315	400	500
Ряд 2	56	71	90	112	140	180	225	355	560

1.5.2 Предварительно значение диаметра внешней делительной окружности шестерни

d_e1'=d_e2/u

1.5.3 Число зубьев шестерни и колеса

1.5.3.1 Число зубьев шестерни

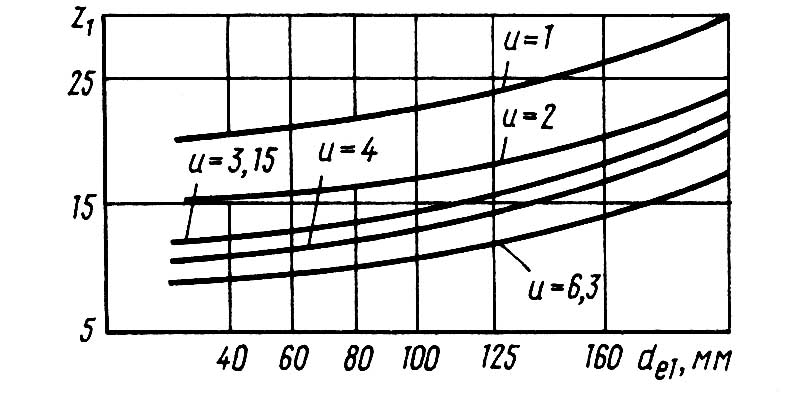
Предварительное значение зубьев шестерни z₁' для колес выбирают по рис.8 в зависимости от диаметра d_e1' шестерни.

Рис.8. График для определения числа зубьев шестерни

Затем предварительное значение числа зубьев шестерни z₁' уточняют в соответствии с табл.6.

Таблица 6

Число зубьев шестерни в зависимости от термической обработки колес

		Значение z₁'
Шестерня	HHRC45	z₁=z₁'
Колесо
Шестерня	HHRC45	z₁=1,3_*z₁'
Колесо	HHB350
Шестерня	H<HB350	z₁=1,6_*z₁'
Колесо

Значение z₁ округлить до целого числа. z_1min12.

1.5.3.2 Число зубьев колеса

z'₂=z_1*u

Значение z'₂ округлить до целого числа.

1.5.4 Фактическое передаточное число

u_ф=z₂/z₁

Разность между расчетным и фактическим передаточными числами:

u=(u-u_ф)/u_*100%3%

1.5.5 Углы делительных конусов шестерни и колеса, град

₂=arctgu

₁=90⁰-₂

1.5.6 Внешний окружной модуль, мм

m_te=d_e₂/z₂

Внешний окружной модуль m_te может иметь нестандартное значение, но на практике значение m_te принимают ближайшее стандартное из стандартного ряда чисел (табл.7).

Таблица 7

Модуль передачи

Ряд 1	1,5	2	2,5	3	4	5	6	8	10
Ряд 2	1,75	2,25	2,75	3,5	4,5	5,5	7	9	11

1.5.7 Число зубьев плоского колеса

1.5.8 Окончательное значение диаметра внешней делительной окружности шестерни

Точность расчета – 0,001 мм.

d_e₁=m_te_*z₁

1.5.9 Внешнее конусное расстояние, мм

Величину R_e не округлять.

1.5.10 Ширина зубчатого венца (предварительная), мм

b'0,3_*R_e

Принять ближайшее из стандартного ряда Ra20: 15, 18, 20, 22, 25, 28, 32, 36, 40, 45, 50, 56, 63, 71, 80, 90, 100, 110, 125, 140, 160, 180, 200, 220 – только для редукторов в крупносерийном и массовом производствах. Для редукторов индивидуального производства значении b округлить до целого значения.

1.5.11 Уточнить значение коэффициента ширины зубчатого венца

_bR=b/R_e10_*m_te

1.5.12 Среднее конусное расстояние, мм

R_m=R_e-0,5_*b

1.5.13 Средний нормальный модуль, мм

где _m – угол наклона зубьев в среднем сечении; рекомендуется принимать _m=35⁰.

1.5.14 Средний делительный диаметр шестерни и колеса, мм

d_m1=m_nm*z₁/cos_m

d_m2=m_nm*z₂/cos_m

1.6 Средняя окружная скорость в зацеплении, м/с

или

В соответствии со значением V_m назначается степень точности n (см.табл.8).

Таблица 8

1.7 Уточнение коэффициента нагрузки

Коэффициент нагрузки при расчете на контактную прочность:

k_H=k_H__*k_H__*k_Hv

Коэффициент нагрузки при расчете на изгибную выносливость:

k_F=k_F__*k_F__*k_Fv

где k_H_, k_F_- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;

k_H_, k_F_- коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;

k_Hv, k_F_v- коэффициент, учитывающий динамическую нагрузку.

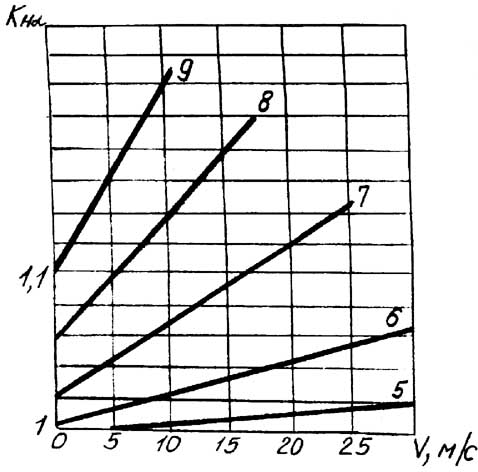
Для косозубых передач и передач с круговыми зубьями коэффициент k_H_ принимают по рис.9 в зависимости от скорости V и степени точности передачи n.

Рис.9. График для определения k_H_

Коэффициент k_F_=1 при коэффициенте осевого перекрытия _1.

при _>1:

где b – рабочая ширина венца;

_m – угол наклона зубьев в среднем сечении, рекомендуется принимать _m=35⁰;

m_nm – модуль средний нормальный;

n – степень точности передачи по нормам контакта;

_ – коэффициент торцового перекрытия:

z₁, z₂ – число зубьев шестерни и колеса.

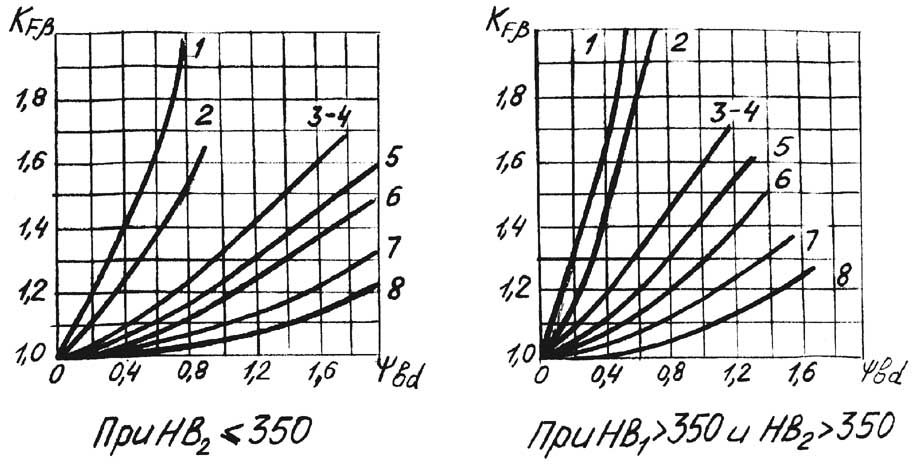
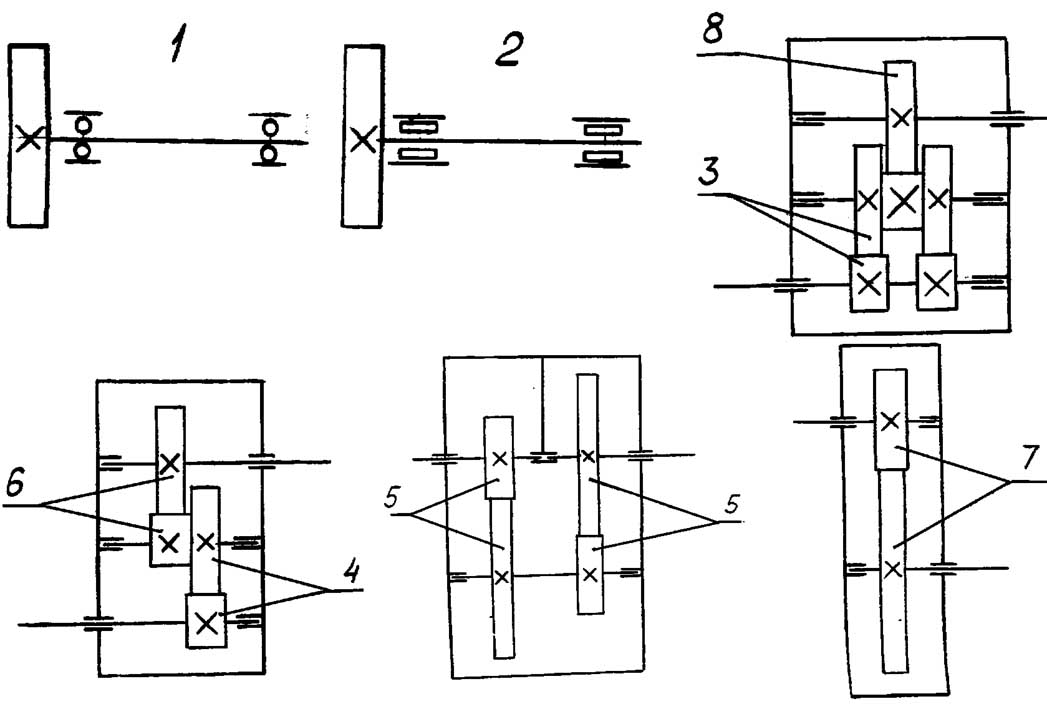
При предварительном расчете коэффициенты k'_H_ и k'_F_ определяют соответственно по рис.10 и рис.11 в зависимости от схемы передачи рис.11 и относительной ширины шестерни _bd:

где _bR=b/R_e0,3 – коэффициент относительной ширины зубчатых колес;

рекомендуется принимать при предварительном расчете _bR=0,285.

Рис.10. График определения k_H_

Рис.11. График определения k_F_

Рис.12. Схемы расположения передач

При уточненном расчете:

k_H_=1+(k^o_H_-1)_*k_H_

k_F_=1+(k^o_F_-1)_*k_F_

где k^o_H_, k^o_F_ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца в начальный период работы передачи; определяется по табл.9.

Таблица 9

Значение коэффициентов koH и koF

b/d₁	HB₂	Схема передачи (рис.12)
b/d₁	HB₂	1	2	3	4	5	6	7	8
0,2	350	1,70/1,53	1,40/1,31	1,30/1,23	1,18/1,15	1,08/1,07	1,05/1,04	1,05/1,04	1,05/1,04
0,2	>350	1,35/1,25	1,20/1,16	1,15/1,12	1,09/1,08	1,05/1,04	1,05/1,04	1,05/1,04	1,05/1,04
0,4	350	2,40/2,01	1,90/1,67	1,60/1,46	1,36/1,27	1,20/1,16	1,12/1,09	1,08/1,06	1,05/1,04
0,4	>350	1,70/1,53	1,45/1,34	1,30/1,23	1,18/1,13	1,10/1,08	1,06/1,05	1,05/1,04	1,05/1,04
0,6	350	3,10/2,47	2,40/2,01	2,00/1,74	1,60/1,46	1,34/1,26	1,24/1,16	1,14/1,08	1,06/1,06
0,6	>350	2,05/1,75	1,70/1,53	1,50/1,38	1,30/1,23	1,17/1,14	1,12/1,08	1,07/1,06	1,05/1,04
0,8	350	4,00/3,03	3,00/2,41	2,40/2,01	1,86/1,62	1,54/1,41	1,40/1,31	1,26/1,21	1,10/1,08
0,8	>350	2,50/2,08	2,00/1,74	1,70/1,53	1,43/1,32	1,27/1,21	1,20/1,16	1,13/1,08	1,05/1,04
1,0	350	- / -	3,60/2,80	2,80/2,28	2,12/1,82	1,80/1,60	1,60/1,46	1,40/1,31	1,20/1,16
1,0	>350	- / -	2,30/1,95	1,90/1,67	1,56/1,42	1,40/1,31	1,30/1,23	1,20/1,16	1,10/1,08
1,2	350	- / -	- / -	3,20/2,54	2,44/2,04	2,08/1,80	1,80/1,60	1,60/1,46	1,30/1,23
1,2	>350	- / -	- / -	2,10/1,81	1,72/1,53	1,54/1,42	1,40/1,31	1,30/1,23	1,15/1,11
1,4	350	- / -	- / -	- / -	2,80/2,28	2,40/2,01	2,00/1,76	1,80/1,60	1,42/1,32
1,4	>350	- / -	- / -	- / -	1,90/1,67	1,70/1,53	1,52/1,40	1,40/1,31	1,21/1,16
1,6	350	- / -	- / -	- / -	- / -	2,80/2,23	2,40/2,01	2,00/1,74	1,60/1,46
1,6	>350	- / -	- / -	- / -	- / -	1,90/1,67	1,70/1,50	1,50/1,38	1,30/1,23
Примечание. Значение в числителе для k^o_H_, в знаменателе для k^o_F_.

k_H_, k_F_ – коэффициент, учитывающий приработку зубьев.

Коэффициент k_H_ определяют по рис.13.

Рис.13. График определения k_H_

Рис.14. График определения k_F_

Коэффициент k_F_=1 при НВ₁>350HB и HB₂>350HB.

При НВ₁350НВ и НВ₂350НВ k_H_ определяют по рис.14.

При различных твердостях рабочих поверхностей зубьев шестерни и колеса принимают меньшую величину твердости.

При НВ<200НВ принимают НВ=200НВ.

k_HV, k_FV– коэффициент, учитывающий динамическую нагрузку; определяется по табл.10 в зависимости от окружной скорости колеса Vи степени точности.

Таблица 10

Значение коэффициентов kHv и kFv

Степень точности	HB₂	Коэффициент	Окружная скорость v
Степень точности	HB₂	Коэффициент	1	2	4	6	8	10
6	350	K_Hv	1,01	1,02	1,03	1,04	1,06	1,07
	350	K_Fv	1,02	1,05	1,10	1,15	1,20	1,25
	>350	K_Hv	1,00	1,00	1,02	1,02	1,03	1,04
	>350	K_Fv	1,01	1,02	1,03	1,04	1,06	1,07
7	350	K_Hv	1,02	1,03	1,05	1,06	1,07	1,08
	350	K_Fv	1,03	1,06	1,11	1,16	1,22	1,27
	>350	K_Hv	1,00	1,01	1,02	1,03	1,03	1,04
	>350	K_Fv	1,01	1,02	1,03	1,05	1,07	1,08
8	350	K_Hv	1,01	1,02	1,04	1,06	1,07	1,08
	350	K_Fv	1,03	1,06	1,11	1,17	1,23	1,29
	>350	K_Hv	1,01	1,01	1,02	1,03	1,04	1,05
	>350	K_Fv	1,01	1,02	1,03	1,05	1,07	1,08
9	350	K_Hv	1,01	1,03	1,05	1,07	1,09	1,12
	350	K_Fv	1,04	1,07	1,14	1,21	1,28	1,35
	>350	K_Hv	1,01	1,01	1,02	1,03	1,04	1,05
	>350	K_Fv	1,01	1,02	1,04	1,06	1,08	1,09

1.8 Расчетное контактное напряжение, мПа

где Z_H –коэффициент учитывающий форму сопряженных поверхностей зубьев;

;

_Н– коэффициент, учитывающий вид конической передачи;

Z_M– коэффициент, учитывающий механические свойства материалов сопряженных зубьев;

Z_M=275МПа;

Z_– коэффициент, учитывающий суммарную длину контактных линий;

здесь _ – коэффициент торцового перекрытия.

Допускаемая недогрузка передачи (_Н<[]_Н) не более 16% и перегрузка (_Н>[]_Н) не более 5%. Если условие прочности не выполняется, то следует изменить ширину венца колеса и шестерни b. Если эта мера не даст должного результата, то либо надо увеличить внешний делительный диаметр колеса d_e2, либо назначить другие материалы колес или другую термообработку, пересчитать допускаемые контактные напряжения и повторить весь расчет передачи.

1.9 Геометрические размеры шестерни и колеса

Для конических передач с разностью средних твердостей шестерни и колеса НВ_1ср-НВ_2ср100 коэффициент смешения инструмента х_n₁для шестерни выбирают по табл.11.

Коэффициент смещения нормальный х_n1=-х_n2или

х_n₁=-х_n₂=0,49_*cos_m_*(1-1/u²) – для равновысоких зубьев.

Таблица 11

Коэффициент смешения хn1 для шестерни конических передач

z₁	х_n1 при передаточном числе u
z₁	2,0	2,5	3,15	4,0	5,0
12	-	0,50	0,53	0,56	0,57
12	0,44	0,48	0,52	0,54	0,55
14	0,42	0,47	0,50	0,52	0,53
15	0,40	0,45	0,48	0,50	0,51
16	0,38	0,43	0,46	0,48	0,49
18	0,36	0,40	0,43	0,45	0,46
20	0,34	0,37	0,40	0,42	0,43
25	0,29	0,33	0,36	0,38	0,39
30	0,25	0,28	0,31	0,33	0,34
40	0,20	0,22	0,24	0,26	0,27

1.9.1 Высота головки зуба в среднем сечении, мм:

h_am1=(h_a^*+x_n1)_*m_nm

h_am2=(h_a^*+x_n2)_*m_nm

где h_a^*=1 – коэффициент высоты головки зуба.

1.9.2 Высота ножки зуба в среднем сечении, мм:

h_fm₁=(h_a^*+с^*-x_n₁)_*m_nm

h_fm₂=(h_a^*+с^*-x_n₂)_*m_nm

где с^*=0,25 – коэффициент радиального зазора.

1.9.3 Угол ножки зуба, град:

_f1=arctg(h_fm1/R_m)

_f2=arctg(h_fm2/R_m)

1.9.4 Угол головки зуба, град:

_a1=_f2

_a2=_f1

1.9.5 Угол конуса вершин, град:

_a₁=₁+_a₁

_a₂=₂+_a₂ – для нормально понижающихся зубьев;

или

_a₁=₁

_a₂=₂ – для равновысоких зубьев

1.9.6 Угол конуса впадин, град:

_f₁=₁-_f₁

_f₂=₂-_f₂– для нормально понижающихся зубьев;

или

_f₁=₁

_f₂=₂– для равновысоких зубьев

1.9.7 Увеличение высоты головки зуба при переходе от среднего сечения к внешнему торцу, мм:

h_ae1=0,5_*b_*tg_a1

h_ae2=0,5_*b_*tg_a2

1.9.8 Увеличение высоты ножки зуба при переходе от среднего сечения к внешнему торцу, мм:

h_fe1=0,5_*b_*tg_f1=h_ae2

h_fe2=0,5_*b_*tg_f2=h_ae1

1.9.9 Внешняя высоты головки зуба, мм:

h_ae₁=h_am₁+h_ae₁

h_ae₂=h_am₂+h_ae₂ – для нормально понижающихся зубьев;

или

h_ae₁=h_am₁

h_ae₂=h_am₂– для равновысоких зубьев

1.9.10 Внешняя высоты ножки зуба, мм:

h_fe₁=h_fm₁+h_fe₁

h_fe₂=h_fm₂+h_fe₂ – для нормально понижающихся зубьев;

или

h_fe₁=h_fm₁

h_fe₂=h_fm₂– для равновысоких зубьев;

1.9.11 Внешняя высота зуба, мм:

h_e1=h_ae1+h_fe1

h_e2=h_ae2+h_fe2

1.9.12 Внешний делительный диаметр, мм:

d_e1=m_te*z₁

d_e2=m_te*z₂

1.9.13 Внешний диаметр вершин, мм:

d_ae1=d_e1+2_*h_ae1cos₁

d_ae2=d_e2+2_*h_ae2cos₂

1.9.14 Внешний диаметр впадин, мм:

d_fe1=d_e1-2_*h_fe1cos₁

d_fe2=d_e2-2_*h_fe2cos₂

1.10 Расчетное напряжение изгиба в зубьях шестерни и колеса, мПа

где Y_F1, Y_F2- коэффициент формы зуба шестерни и колеса, принимаются по таблице 12, в зависимости от эквивалентного числа зубьев z_v1 и z_v2

Таблица 12

Коэффициент формы зуба yf

z_v	Коэффициент смещения режущего инструмента Х_е
z_v	-0,5	-0,4	-0,3	-0,2	-0,1	0	+0,1	+0,2	+0,3	+0,4	+0,5
12	-	-	-	-	-	-	-	-	3,9	3,67	3,46
14	-	-	-	-	-	-	4,24	4	3,78	3,59	3,42
17	-	-	-	-	4,5	4,27	4,03	3,83	3,67	3,53	3,4
20	-	-	-	4,55	4,28	4,07	3,89	3,75	3,61	3,5	3,39
25	-	4,6	4,39	4,2	4,04	3,9	3,77	3,67	3,57	3,48	3,39
30	4,6	4,32	4,15	4,05	3,9	3,8	3,7	3,62	3,55	3,47	3,4
40	4,12	4,02	3,92	3,84	3,77	3,7	3,64	3,58	3,53	3,48	3,42
50	3,97	3,88	3,81	3,76	3,7	3,65	3,61	3,57	3,53	3,49	3,44
60	3,85	3,79	3,73	3,7	3,66	3,63	3,59	3,56	3,53	3,5	3,46
80	3,73	3,7	3,68	3,65	3,62	3,61	3,58	3,56	3,54	3,52	3,5
100	3,68	3,67	3,65	3,62	3,61	3,6	3,58	3,57	3,55	3,53	3,52

Y_ – коэффициент, учитывающий наклон зубьев;

;

_F – коэффициент вида конических колес;

_F=1…1,2 – большие значения для колес с твердостью менее 350НВ;

k_F – коэффициент нагрузки;

[]_F₁, []_F₂ – допускаемые напряжения изгиба для шестерни и колеса (см.1.3).

1.11 Усилия в зацеплении

1.11.1 Окружная сила

F_t1=-F_t2=2_*T_1*10³/d_m1, H

1.11.2 Радиальная сила на шестерне, равная осевой силе на колесе

F_r₁=-F_a₂=F_t_1*(tg_*cos₁-sin_m_*sin₁)/cos_m, H – направление вращения совпадает с направлением линии наклона зуба

или

F_r₁=-F_a₂=F_t_1*(tg_*cos₁+sin_m_*sin₁)/cos_m, H – направление вращения и линия наклона зуба противоположны

где =20⁰ – угол зацепления.

1.11.3 Осевая сила на шестерне, равная радиальной силе на колесе

F_a₁=-F_r₂=F_t_1*(tg_*sin₁+sin_m_*cos₁)/cos_m, H – направление вращения совпадает с направлением линии наклона зуба

или

F_a₁=-F_r₂=F_t_1*(tg_*sin₁-sin_m_*cos₁)/cos_m, H – направление вращения и линия наклона зуба противоположны.

1.12 Проверка передачи на прочность при кратковременной перегрузке

1.12.1 Максимальные контактные напряжения, МПа

где Т₁_max – максимальный вращающий момент на валу шестерни;

здесь Р_дв – номинальная мощность электродвигателя;

n_дв – номинальная частота вращения вала электродвигателя;

– отношение берут из справочника по электродвигателям;

u,  – передаточное число и коэффициент полезного действия ступеней, через которые передается движение от вала электродвигателя к валу шестерни;

Т₁ – номинальный вращающий момент на валу шестерни;

здесь Р_дв.р. – расчетная мощность электродвигателя;

[]_H_max – предельное допустимое контактное напряжение;

[]_Hmax=2,8_*_т – для зубчатых колес, подвергнутых нормализации, улучшению или сквозной закалке с низким отпуском;

[]_Hmax=44_*H_HRC – для зубьев подвергнутых цементации или контурной закалке;

[]_Hmax=3_*H_HV – для азотированных зубьев;

_т – предел текучести (см.табл.1).

1.12.2 Максимальные напряжения изгиба, МПа

где []_F_max – предельное допустимое напряжение изгиба;

[]_Fmax=0,8_*_т – при твердости поверхности зубьев 350HB;

[]_Fmax=0,6_*_в – при твердости поверхности зубьев >350HB;

_в – предел прочности при растяжении (см.табл.1).

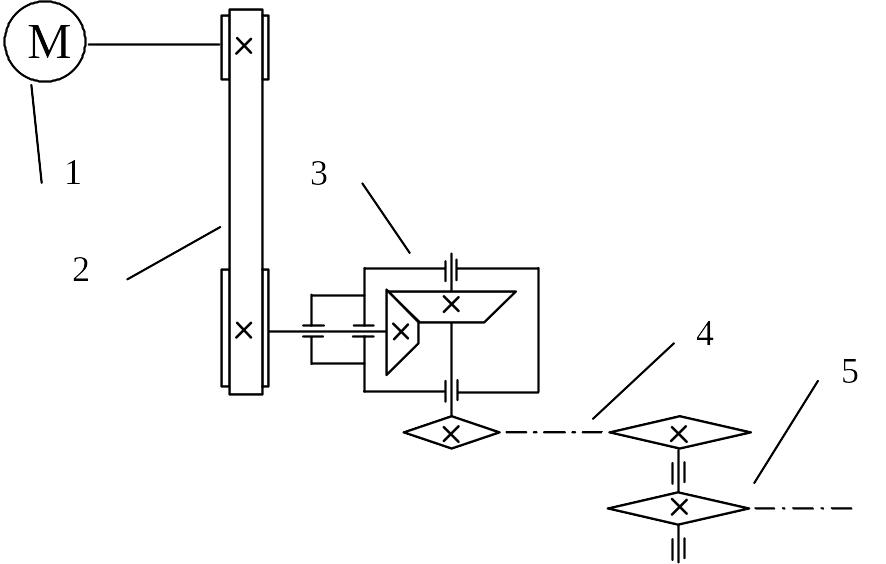
2 Пример расчета конической передачи с круговыми зубьями Задание: Выполнить расчет конической передачи с круговыми зубьями редуктора привода к цепному конвейеру при следующих данных:

Исходные данные:

Номинальная мощность электродвигателя	Р_дв=2,2 кВт
Номинальная частота вращения вала электродвигателя	n_дв=1425 об/мин
Мощность на валу шестерни	Р₁=2,07 кВт
Частота вращения шестерни	n₁=475 об/мин
Угловая скорость шестерни	w₁=49,72 рад/с
Частота вращения колеса	n₂=150,8 об/мин
Угловая скорость колеса	w₂=15,78 рад/с
Вращающий момент на шестерне	Т₁=41,63 Н_*м
Вращающий момент на колесе	Т₂=125,97 Н_*м
Передаточное число ременной передачи	U₁=3
Передаточное число рассчитываемой передачи	U₂=3,15
Коэффициент перегрузки
Срок службы передачи	t_=15_*10³ ч
Режим работы	Постоянный
Передача	Не реверсивная

2.1 Материал шестерни и колеса

2.1.1 Шестерня: материал – сталь 40Х, термообработка – улучшение, НВ269…302 (НВ_1ср285,5), _В=900МПа, _Т=750МПа.

[1,с.6]

2.1.2 Колесо: материал – сталь 40Х, термообработка – улучшение, НВ235…262 (НВ_2ср245,5), _В=790МПа, _Т=640МПа.

[1,с.6]

2.2 Допускаемые контактные напряжения

где _H_limb– предел контактной выносливости поверхности зубьев, соответствующий базовому числу циклов перемены напряжений;

_Hlimb=2_*НВ+70 [1,с.7]

_Hlimb1=2_*285,5+70=641МПа

_Hlimb2=2_*248,5+70=567МПа

S_H – коэффициент запаса прочности:

для колеса с однородной структурой материала: S_H=1,1; [1,с.7]

Z_R– коэффициент, учитывающий шероховатость сопряженных поверхностей зубьев;

Z_V– коэффициент, учитывающий окружную скорость;

Z_L– коэффициент, учитывающий влияние смазки;

Z_X– коэффициент, учитывающий размер зубчатого колеса;

При расчете допускаемых контактных напряжений следует принимать Z_R_*Z_V_*Z_L_*Z_X=0,9. [1,с.8]

Z_N– коэффициент долговечности:

где N_HO – базовое число циклов перемены напряжений, соответствующее пределу выносливости:

N_HO=30_*HB_cp^2,4[1,с.9]

N_HO₁=30_*285,5^2,4=23,5_*10⁶

N_HO₂=30_*248,5^2,4=16,8_*10⁶

N_HE- эквивалентное число циклов перемены напряжений за весь срок службы (наработка), млн. циклов.

При постоянной нагрузке:

N_HE=60_*c_*n_i*t_,

здесь с – число одинаковых колес, сцепляющихся с рассчитываемым;

с=1

n_i – частота вращения рассчитываемого колеса;

n₁=475об/мин

n₂=150,8об/мин

t_– срок службы привода (ресурс);

t_=15_*10³ ч;

N_HE1=60_*1_*475_*15_*10³=427,5_*10⁶

N_HE₂=60_*1_*150,8_*15_*10³=135,7_*10⁶

m_H – показатель корня;

При N_HE>N_HO m_H=20:

[]_H=0,45_*([]_H1+[]_H2)1,15_*[]_H2

[]_H=0,45_*(454+418)=392МПа1,15_*418=480,7МПа

2.3 Допускаемые напряжения изгиба

где _Flimb– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений:

_Flimb=1,8_*HB [1,с.7]

_Flimb1=1,8_*285,5=514МПа

_Flimb2=1,8_*248,5=447,3МПа

S_F – коэффициент запаса прочности:

S_F=1,9; [1,с.10]

Y_R – коэффициент, учитывающий влияние шероховатости поверхности;

Y_R=1 – для шлифования и зубофрезерования при шероховатости не более Rz=40мкм; [1,с.10]

Y_C– коэффициент, учитывающий двухстороннее приложение нагрузки безопасности;

Y_С=1 – при одностороннем приложении нагрузки; [1,с.10]

Y_N– коэффициент долговечности:

здесь N_FO – базовое число циклов перемены напряжений, соответствующее пределу выносливости,

N_FO=4_*10⁶; [1,с.7]

N_FE- эквивалентное число циклов перемены напряжений за весь срок службы (наработка).

m_F – показатель корня;

m_F=6 – при твердости поверхности зубьев 350НВ; [1,с.11]

При постоянной нагрузке:

N_FE=60_*c_*n_i*t_, т.е. N_FE=N_HE:

N_FE1=N_HE1=427,5_*10⁶

N_FE2=N_HE2=135,7_*10⁶

При N_F_EN_F_O коэффициент долговечности Y_N=1; [1,с.11]

2.4 Проектный расчет закрытой конической передачи с круговыми зубьями

2.4.1 Внешний делительный диаметр колеса

где Т₂=125,97Н_*м;

u=3,15;

k'_HB – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца (предварительный);

Коэффициент относительной ширины шестерни _bd:

Углы делительных конусов шестерни и колеса:

₂=arctg u=arctg 3,15=72,39⁰;

₁=90⁰-72,39⁰=17,61⁰;

k'_HB=1,2; [1,с.15]

_Н– коэффициент, учитывающий вид конической передачи;

_Н=1,2+0,2_*u – для конических колес при твердость менее 350НВ;

_Н=1,2+0,2_*3,15=1,83;

[]_H=392 МПа;

Принимаем d_e2=200мм. [1,с.12]

2.4.2 Предварительно значение диаметра внешней делительной окружности шестерни

d_e1'=d_e2/u=200/3,15=63,5мм

2.4.3 Число зубьев шестерни и колеса

2.4.3.1 Число зубьев шестерни

Предварительное значение зубьев шестерни:

z₁'=18 [1,с.12]

Уточненное значение зубьев шестерни:

z₁=1,6_*z₁'=1,6_*18=28,8 [1,с.12]

Принимаем z₁=29.

2.4.3.2 Число зубьев колеса

z'₂=z_1*u=29_*3,15=91,35

Принимаем z₂=91.

2.4.4 Фактическое передаточное число

u_ф=z₂/z₁=91/29=3,14

Разность между расчетным и фактическим передаточными числами:

u=(u-u_ф)/u_*100%

=(3,15-3,14)/3,15_*100%=0,31%3%

2.4.5 Внешний окружной модуль

m_te=d_e₂/z₂=200/91=2,197 мм

Принимаем m_te=2,25мм [1,с.13]

2.4.6 Число зубьев плоского колеса

2.4.7 Окончательное значение диаметра внешней делительной окружности шестерни

d_e1=m_te*z₁=2,25_*29=65,25мм

2.4.8 Внешнее конусное расстояние

2.4.9 Ширина зубчатого венца (предварительная)

b'0,3_*R_e=0,3_*107,449=32,23мм

Принимаем b=32мм [1,с.13]

2.4.10 Уточнить значение коэффициента ширины зубчатого венца

_bR=b/R_e10_*m_te

_bR=32/107,449=0,29810_*2,25=22,5

2.4.11 Среднее конусное расстояние

R_m=R_e-0,5_*b=107,449-0,5_*32=91,449мм

2.4.12 Средний нормальный модуль

где _m – угол наклона зубьев в среднем сечении; рекомендуется принимать _m=35⁰.

2.4.13 Средний делительный диаметр шестерни и колеса

d_m1=m_nm*z₁/cos_m=1,57_*29/cos35⁰=55,58мм

d_m2=m_nm*z₂/cos_m=1,57_*91/cos35⁰=174,41мм

2.5 Средняя окружная скорость в зацеплении

Степень точности n=8. [1,с.14]

2.6 Уточнение коэффициента нагрузки

Коэффициент нагрузки при расчете на контактную прочность:

k_H=k_H__*k_H__*k_Hv

Коэффициент нагрузки при расчете на изгибную выносливость:

k_F=k_F__*k_F__*k_Fv

где k_H_, k_F_- коэффициент, учитывающий неравномерность распределения нагрузки между зубьями;

k_H_= 1,09 [1,с.14]

Коэффициент осевого перекрытия

поэтому

здесь _ – коэффициент торцового перекрытия:

n – степень точности передачи по нормам контакта;

n=8;

;

k_H_, k_F_- коэффициент, учитывающий неравномерность распределения нагрузки по ширине зуба;

k_H_=1+(k^o_H_-1)_*k_H_,

k_F_=1+(k^o_F_-1)_*k_F_,

здесь k^o_H_, k^o_F_ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца в начальный период работы передачи;

k^o_H_=2,4 [1,с.16]

k^o_F_=2,01 [1,с.16]

k_H_, k_F_ – коэффициент, учитывающий приработку зубьев;

k_H_=0,35 [1,с.17]

k_F_=0,45 [1,с.17]

k_H_=1+(2,4-1)_*0,35=1,49

k_F_=1+(2,01-1)_*0,45=1,45

k_Hv, k_F_v- коэффициент, учитывающий динамическую нагрузку.

k_Hv=1,02 [1,с.17]

k_Fv=1,06 [1,с.17]

k_H=1,09_*1,49_*1,02=1,66

k_F=0,926_*1,45_*1,06=1,42

2.7 Расчетное контактное напряжение

где Z_H –коэффициент учитывающий форму сопряженных поверхностей зубьев;

;

_Н=1,83;

Z_M– коэффициент, учитывающий механические свойства материалов сопряженных зубьев;

Z_M=275МПа;

Z_– коэффициент, учитывающий суммарную длину контактных линий;

2.8 Геометрические размеры шестерни и колеса

Коэффициент смещения нормальный х_n1=-х_n2=0,31. [1,с.18]

2.8.1 Высота головки зуба в среднем сечении

h_am1=(h_a^*+x_n1)_*m_nm

h_am2=(h_a^*+x_n2)_*m_nm

где h_a^*=1 – коэффициент высоты головки зуба.

h_am1=(1+0,31)_*1,57=2,15мм

h_am2=(1+0,31)_*1,57=1,08мм

2.8.2 Высота ножки зуба в среднем сечении

h_fm₁=(h_a^*+с^*-x_n₁)_*m_nm

h_fm₂=(h_a^*+с^*-x_n₂)_*m_nm

где с^*=0,25 – коэффициент радиального зазора.

h_fm₁=(1+0,25-0,31)_*1,57=1,48мм

h_fm₂=(1+0,25-0,31)_*1,57=2,45мм

2.8.3 Угол ножки зуба

_f1=arctg(h_fm1/R_m)=arctg(1,48/91,449)=0,927⁰

_f2=arctg(h_fm2/R_m)=arctg(2,45/91,449)=1,54⁰

2.8.4 Угол головки зуба

_a₁=_f₂=1,54⁰

_a₂=_f₁=0,927⁰

2.8.5 Угол конуса вершин

_a1=₁+_a1=17,61⁰+1,54⁰=19,15⁰

_a2=₂+_a2=72,39⁰+0,927⁰=73,32⁰

2.8.6 Угол конуса впадин

_f₁=₁-_f₁=17,61⁰-0,927⁰=16,68⁰

_f₂=₂-_f₂=72,39^0-1,54⁰=70,85⁰

2.8.7 Увеличение высоты головки зуба при переходе от среднего сечения к внешнему торцу

h_ae1=0,5_*b_*tg_a1=0,5_*32_*tg1,54⁰=0,43мм

h_ae2=0,5_*b_*tg_a2=0,5_*32_*tg0,927⁰=0,26мм

2.8.8 Увеличение высоты ножки зуба при переходе от среднего сечения к внешнему торцу

h_fe1=0,5_*b_*tg_f1=h_ae2=0,26мм

h_fe2=0,5_*b_*tg_f2=h_ae1=0,43мм

2.8.9 Внешняя высоты головки зуба

h_ae1=h_am1+h_ae1=2,15+0,43=2,58мм

h_ae2=h_am2+h_ae2=1,08+0,26=1,34мм

2.8.10 Внешняя высоты ножки зуба

h_fe1=h_fm1+h_fe1=1,48+0,26=1,74мм

h_fe2=h_fm2+h_fe2=2,45+0,43=2,88мм

2.8.11 Внешняя высота зуба

h_e₁=h_ae₁+h_fe₁=2,58+1,74=4,32мм

h_e2=h_ae2+h_fe2=1,34+2,88=4,22мм

2.8.12 Внешний делительный диаметр

d_e₁=m_te_*z₁=2,25_*29=65,25мм

d_e2=m_te*z₂=2,25_*91=204,75мм

2.8.13 Внешний диаметр вершин

d_ae1=d_e1+2_*h_ae1cos₁=65,25+2_*2,58_*cos17,61⁰=70,17мм

d_ae2=d_e2+2_*h_ae2cos₂=204,75+2_*1,34_*cos72,39⁰=205,56мм

2.8.14 Внешний диаметр впадин

d_fe1=d_e1-2_*h_fe1cos₁=65,25-2_*1,74_*cos17,61⁰=61,93мм

d_fe2=d_e2-2_*h_fe2cos₂=204,75-2_*2,88_*cos72,39⁰=203,01мм

2.9 Расчетное напряжение изгиба в зубьях шестерни и колеса

где Y_F1, Y_F2- коэффициент формы зуба шестерни и колеса;

Y_F1=3,65

Y_F2=3,6 [1,с.20]

Y_ – коэффициент, учитывающий наклон зубьев;

;

_F – коэффициент вида конических колес;

_F=1…1,2 – большие значения для колес с твердостью менее 350НВ;

_F=1,2;

k_F =1,42;

2.10 Усилия в зацеплении

2.10.1 Окружная сила

F_t1=-F_t2=2_*T_1*10³/d_m1=2_*41,63_*10³/55,58=1498,02 H

2.10.2 Радиальная сила на шестерне, равная осевой силе на колесе

F_r₁=-F_a₂=F_t_1*(tg_*cos₁-sin_m_*sin₁)/cos_m – направление вращения совпадает с направлением линии наклона зуба

где =20⁰ – угол зацепления

F_r₁=-F_a₂=1498,02_*(tg20⁰_*cos17,61⁰-sin35⁰_*sin17,61⁰)/cos35⁰=317,08Н

2.10.3 Осевая сила на шестерне, равная радиальной силе на колесе

F_a₁=-F_r₂=F_t_1*(tg_*sin₁+sin_m_*cos₁)/cos_m – направление вращения совпадает с направлением линии наклона зуба

F_a1=-F_r2=1498,02_*(tg20⁰_*sin17,61⁰+sin35⁰_*cos17,61⁰)/cos35⁰=1201,14Н

2.11 Проверка передачи на прочность при кратковременной перегрузке

2.11.1 Максимальные контактные напряжения

где Т₁_max – максимальный вращающий момент на валу шестерни;

здесь Р_дв=2,2кВт – номинальная мощность электродвигателя;

n_дв=1425об/мин – номинальная частота вращения вала электродвигателя;

;

u = u₁= 3

 = _{1 *}₂,

здесь ₁ = 0,95 – к.п.д., учитывающий потери в ременной передаче;

₂ = 0,99 – к.п.д., учитывающий потери в одной паре подшипников качения;

 = 0, 95_*0,99= 0,94;

Т₁ – номинальный вращающий момент на валу шестерни;

Т₁=41,63 Нм

[]_H_max – предельное допустимое контактное напряжение;

[]_H
max=2,8_*_т=2,8_*640=1792МПа

1.12.2 Максимальные напряжения изгиба, МПа

где Т₂_max – максимальный вращающий момент на валу колеса;

Т_2max= Т_1max*u_2*_3*₂,

здесь ₃=0,97 – к.п.д. учитывающий потери в конической передаче;

Т₂_max= 91,3_*3,15_*0,97_*0,99=276,2Нм

Т₂=125,97 Н_*м

[]_F_max – предельное допустимое напряжение изгиба;

[]_F₁_max=0,8_*750=600МПа;

[]_F₂_max=0,8_*640=512МПа

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2025160.77 Кб0Задание для театрализованного урока в 5 классе!...doc
#
12.04.2015303.2 Кб27Задание_на_курсовую_работу.pdf
#
25.11.2019308.22 Кб26Задания к экзамену по элементарной математике.doc
#
01.05.2025106.5 Кб0задания методич практики 3 курс 2013.doc
#
01.05.2025402.98 Кб1Задачник_Передача информации в КС.docx
#
01.04.20251.36 Mб1ЗакКонКПер с круговыми зубьями_1201,1502_в.doc
#
01.04.2025775.68 Кб1ЗакЦилПер_1208,1004,1804.doc
#
17.08.201976.56 Кб17ЗАО ОМК.docx
#
01.05.202512.8 Mб0Иван Кириллович Кирило2.docx
#
01.03.2025738.82 Кб1ИЗЛУЧЕНИЯ В ПРОИЗВОДСТВЕ И ЗАЩИТА ОТ НИХ.doc
#
01.05.202594.21 Кб0Изменения-в-экз.билетах-2013год.doc

Передача	Окружная скорость V_m м/с
Передача	До 5 м/с	5…8	8…12,5	Свыше 12,5 м/с
Коническая с круговыми зубьями	8	8	7	6

1 Методика расчета конических передач с круговыми зубьями

1.1 Выбор материала колеса, термообработки и твердости

1.2 Выбор твердости рабочей поверхности зуба

1.2.1 Прямозубые колеса

1.2.3 Косозубые колеса и колеса с круговые зубьями

Механические свойства стали

1.3 Допускаемые контактные напряжения

Значения Hlimb и Flimb

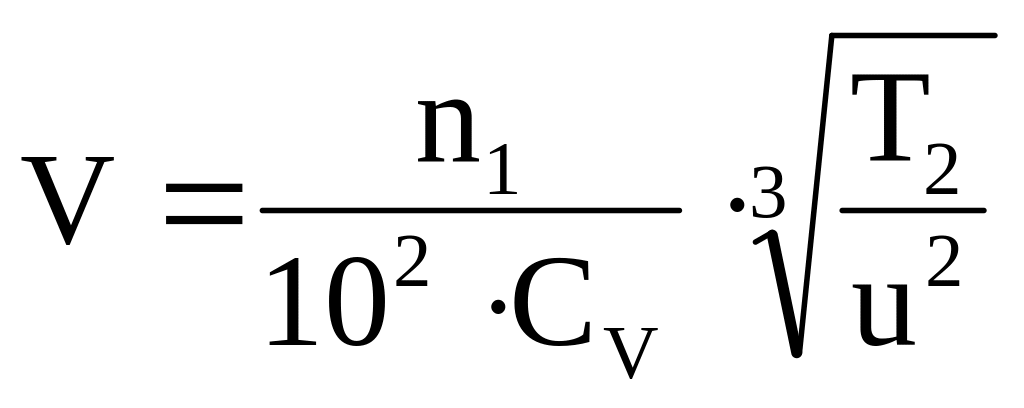
Значение коэффициента сv

Значение коэффициента ba

1.4 Допускаемые напряжения изгиба

1.5 Проектный расчет закрытой конической передачи с круговыми зубьями

Диаметры внешних делительных окружностей

Модуль передачи

1.6 Средняя окружная скорость в зацеплении, м/с

Рекомендуемая степень точности

1.7 Уточнение коэффициента нагрузки

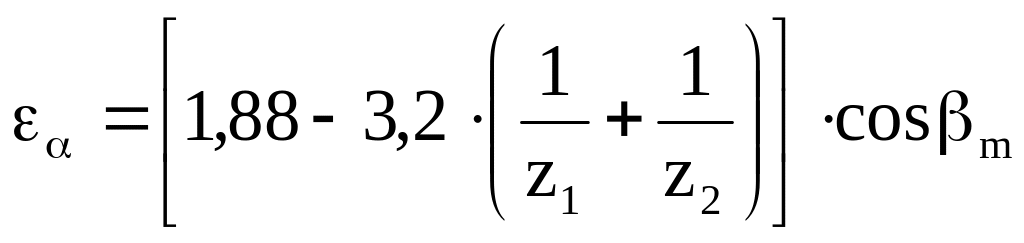
Значение коэффициентов koH и koF

Значение коэффициентов kHv и kFv

1.8 Расчетное контактное напряжение, мПа

1.9 Геометрические размеры шестерни и колеса

Коэффициент смешения хn1 для шестерни конических передач

1.10 Расчетное напряжение изгиба в зубьях шестерни и колеса, мПа

Коэффициент формы зуба yf

1.11 Усилия в зацеплении

1.12 Проверка передачи на прочность при кратковременной перегрузке

2.1 Материал шестерни и колеса

2.2 Допускаемые контактные напряжения

2.3 Допускаемые напряжения изгиба

2.4 Проектный расчет закрытой конической передачи с круговыми зубьями

2.5 Средняя окружная скорость в зацеплении

2.6 Уточнение коэффициента нагрузки

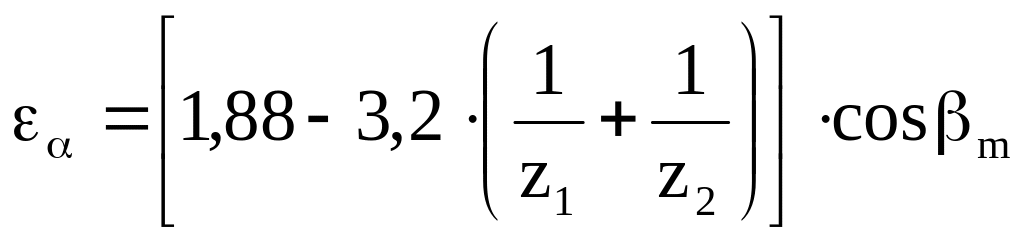
2.7 Расчетное контактное напряжение

2.8 Геометрические размеры шестерни и колеса

2.9 Расчетное напряжение изгиба в зубьях шестерни и колеса

2.10 Усилия в зацеплении

2.11 Проверка передачи на прочность при кратковременной перегрузке