5. Треугольное распределение.

Применимость такого распределения рассмотрим на примере, связанном с динамическими характеристиками системы управления базами данных (СУБД) в экономической информационной системе.

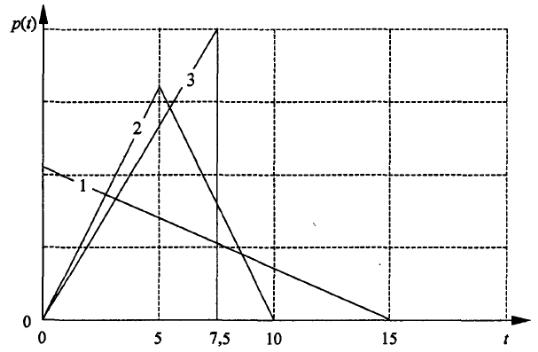
Рис. 1.6. График плотности вероятностей для треугольного распределения:

1 - максимум слева; 2 - максимум в центре; 3 - максимум справа

Пример использования треугольного распределения см. предыдущие лекции.

Выражения для определения математического ожидания М[t] и дисперсии D[t] получаются интегрированием с использованием определений первого и второго моментов:

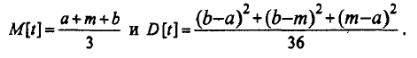
Ниже приведен текст программной функции на C++, возвращающей случайную величину, распределенную по треугольному закону:

f l o a t t r i p l e x ( f l o a t а, float m, float b)

{

float X, r;

г=гип(3глп () ;

if( r <= (m-a)/(b-a). )

X = a + sqrt( r*(m-a)*(b-a) );

else

X = b - sqrt( (1.0-r)*{b-m)*(b-a) );

return(x);

}

Эта программа использует метод обратных функций. Она имеет три входных параметра:

• а - минимально возможное значение интервала времени;

• b - максимально возможное значение интервала времени;

• m - наиболее вероятное значение интервала времени (максимум плотности вероятностей).

Естественно, входные параметры должны удовлетворять следующим условиям: а < m < b .

6. Моделирование случайной величины со ступенчатой плотностью

Часто случайная величина Х определяется по данным наблюдений и в качестве приближения к ее неизвестной плотности берется гистограмма. Рассмотрим способ имитации Х для этого случая.

Рис. 9.4.

Пусть

Пусть F(х) - функция распределения. Геометрически это площадь фигуры, левее вертикальной прямой с абсциссой Х (рис.9.4). При имитации по методу обратной функции значение Х определяется как решение уравнения F(х) = U. Таким образом, надо отыскать такую абсциссу х, чтобы площадь под кривой ( заштрихована на рис. 9.4) равнялась заданному числу U: 0 < U < 1. Если Х попадает в j-й участок, то

,

.

Или

.

Откуда

При этом выражение в скобках отрицательно и j - наименьший индекс, при равенство имеет место. Эта формула и используется для имитации случайной величины X.