Линейная алгебра. Краткий конспект. Лекции 3-4. 8

Линейная алгебра и аналитическая геометрия

Краткий конспект лекций. Сливина Н.А.

Лекции 3- 4. Плоскость и прямая в пространстве Плоскость в пространстве. Уравнения плоскости

В дальнейшем полагаем, что в пространстве определена некая прямоугольная декартова система координат — каждая точка пространства однозначно определена своими координатами.

Уравнение вида — линейное алгебраическое уравнение первой степени или просто — линейное уравнение.

Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору. Пусть задана точка и вектор . Как отличить точки принадлежащие плоскости, проходящей через точку , перпендикулярно вектору , от точек, которые этой плоскости не принадлежат?

Можно предложить такой способ: точка принадлежит плоскости тогда и только тогда, когда вектор ортогонален вектору , т.е. тогда и только тогда, когда .

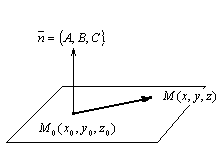
Тогда, поскольку получим линейное уравнение

. Это уравнение плоскости, проходящей через точку нормальным вектором .

Замечание. Вектор, ортогональный плоскости, ортогонален любому вектору, принадлежащему плоскости. Такой вектор называю нормальным вектором плоскости.

Общее уравнение плоскости. Раскроем скобки в уравнении плоскости, проходящей через точку нормальным вектором : и обозначим .

Получим общее уравнение плоскости .

Из предыдущих рассуждений ясно, что коэффициенты общего уравнения плоскости определяют нормальный вектор этой плоскости: .

Задача (Типовой расчет!). Записать уравнение плоскости, проходящей через точку A(2, 5, -3) перпендикулярно вектору , B(7, 8, -1), C(9, 7, 4).

Решение. — нормальный вектор плоскости проходящей через точку A(2, 5, -3). Уравнение плоскости: .

Раскрыв скобки и приведя подобные, получим искомое уравнение

.

Проверим. Точка A(2, 5, -3) принадлежит плоскости: . Нормальный вектор плоскости совпадает с вектором . Задача решена верно.

Ответ. .

Неполные уравнения плоскости. Уравнение определяет плоскость, проходящую через начало координат. Действительно, подставив в уравнение плоскости координаты начала координат, О(0, 0, 0), получим тождество.

Уравнение определяет плоскость, параллельную оси 0x.

Действительно, нормальный вектор этой плоскости ортогонален орту оси 0x — вектору : .

Уравнение — уравнение плоскости, параллельной оси 0y, а

— уравнение плоскости, параллельной оси 0z.

Уравнение — уравнение плоскости, параллельной плоскости y0z, поскольку ее нормальный вектор коллинеарен вектору ;

Уравнение — уравнение плоскости, параллельной плоскости x0z, а уравнение — уравнение плоскости, параллельной плоскости x0y.

Нарисуйте!

Уравнение плоскости в отрезках. Рассмотрим плоскость, которая не проходит через начало координат. Ее уравнение , .

Преобразуем уравнение: , , и обозначим .

Получим уравнение — уравнение плоскости «в отрезках».

Плоскость, заданную таким уравнением легко рисовать. На рисунке изображен случай, когда . Действительно, легко убедиться, что точки с координатами (a, 0,0), (0,b,0), (0,0,c) — это точки пересечения плоскости с координатными осями.

Упражнение. Изобразите сами плоскости, заданные уравнением «в отрезках» для разных сочетаний знаков коэффициентов a, b и c.

Упражнение. Рассмотрите самостоятельно вид уравнения плоскости в отрезках для неполных уравнений , , , , и .

Задача. Изобразить плоскость, заданную уравнением .

Уравнение плоскости, проходящей через три заданные точки. Известно, что три точки, не лежащие на одной прямой, однозначно определяют плоскость.

Как отличить точки принадлежащие плоскости, проходящей через точки , , , от точек, которые этой плоскости не принадлежат? Понятно, что точка принадлежит плоскости тогда и только тогда, когда компланарны векторы , и , т.е. когда .

Поскольку , , , записав смешанное произведение в координатной форме, имеем:

— уравнение плоскости, проходящей через три заданные точки.

Преобразуем уравнение. Поскольку

получим

— линейное уравнение первой степени.

Заметим, что если заданные точки лежат на одной прямой, то векторы и коллинеарны, т.е. все коэффициенты уравнения нулевые и вместо уравнения получим тождество 0 = 0.

Нормальное уравнение плоскости. В уравнении коэффициенты определяют нормальный вектор плоскости: . Длина нормального вектора . Найдем орт нормального вектора плоскости: .

Легко видеть, что координаты орта вектора (орт — вектор единичной длины) равны косинусам углов, образованных этим ортом с положительными направлениями координатных осей:

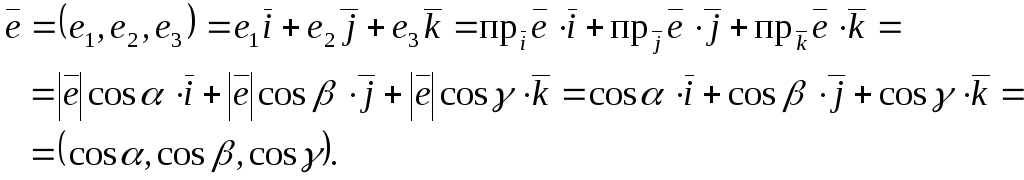
Здесь — углы, образованные ортом с положительными направлениями координатных осей. Косинусы этих углов называются направляющими косинусами вектора.

Т.е. координаты орта нормали к плоскости — направляющие косинусы нормали: .

Здесь — углы, образованные нормалью к плоскостис положительными направлениями координатных осей.

Разделив обе части уравнения на , получим или, см. выше,

— нормальное уравнение плоскости,

.

В нормальном уравнении плоскости коэффициенты при неизвестных — направляющие косинусы нормали, а свободный член p — измеряет расстояние от плоскости до начала координат. Действительно, если точка лежит на плоскости, то ; тогда и .

С другой стороны, расстояние от начала координат до плоскости равно, как легко видеть (см. рис.) .

Угол между плоскостями. Угол между плоскостями равен углу между нормалями к плоскостям. Рассмотрим две плоскости, заданные уравнениями и . Косинус угла между этими плоскостями легко вычислить: , , .

Здесь — угол между плоскостями.

Задача (Типовой расчет!). Найти угол между плоскостями

x + 2y – 2z – 7 =0 и x + y – 35 = 0.

Решение. , , , .

Расстояние между точкой и плоскостью.

Из приведенного рисунка видно, что расстояние от точки до плоскости равно разности длинны проекции радиуса вектора точки на орт нормали к плоскости и расстояния от начала координат до плоскости.

, ,

тогда

Итак, расстояние d от точки до плоскости

вычисляется по формуле .

Задача. Найти расстояние от точки до плоскости x + y – 35 = 0.

Решение. Запишем нормальное уравнение плоскости x + y – 35 = 0:

, , нормальное уравнение плоскости . Тогда расстояние от точки до плоскости —

.

Ответ. Расстояние от точки до плоскости равно .