
Линейная
алгебра. Краткий конспект. Лекции 1-2.
Линейная алгебра и аналитическая геометрия
Краткий конспект лекций. Сливина Н.А.
Лекции 1- 2. Векторная алгебра Геометрические векторы. Линейные операции с векторами
Сначала вспомним известные из школьной программы определения и свойства геометрических векторов.
Определение. Геометрическим вектором называется направленный отрезок.
Обозначаем:
![]() ,
А — начало, B —
конец вектора.
,
А — начало, B —
конец вектора.

Геометрические
векторы также обозначают одной буквой:
![]() и т.п.
и т.п.

Определение.
Длина вектора
![]() — расстояние между точками A
и B.
— расстояние между точками A
и B.
Обозначаем:
![]() и т.п.
и т.п.
Определение. Два вектора называются равными, если они коллинеарны (лежат на параллельных прямых), одинаково направлены и их длины равны.
Обозначаем:
![]() .
.

Определение.
Два вектора называются противоположными,
если они коллинеарны, равны по длине
и противоположно направлены. Обозначаем:
![]() .
.

Определение.
Нулевым называется вектор, имеющий
нулевую длину. Направление нулевого
вектора не определено. Обозначаем:
![]() .
.
Определение.
Суммой векторов
![]() и
и
![]() называется вектор
называется вектор
![]() ,
определенный на рисунке (правило
параллелограмма или правило треугольника).
Обозначаем:
,
определенный на рисунке (правило
параллелограмма или правило треугольника).
Обозначаем:
![]() .
.

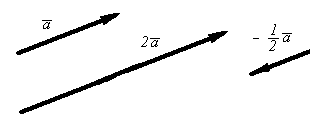
Определение.
Произведением вектора
![]() на число
на число
![]() называется вектор длины
называется вектор длины
![]() ,
коллинеарный вектору
,
коллинеарный вектору
![]() ,
направление которого при
,
направление которого при
![]() совпадает с направлением вектора
совпадает с направлением вектора
![]() ,
а
,
а
![]() — противоположно направлению вектора
— противоположно направлению вектора
![]() .
.
Определение.
Ортом вектора
![]() называется вектор единичной длины,
направление которого совпадает с
направлением вектора
называется вектор единичной длины,
направление которого совпадает с
направлением вектора
![]() .
.
Обозначаем:
![]() и
т.п. Понятно, что
и
т.п. Понятно, что
![]() .
.
Определение. Операции сложения векторов и умножение вектора на число называются линейными операциями с векторами.
Известно (нетрудно доказать), что для линейных операций с векторами справедливо:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
; -
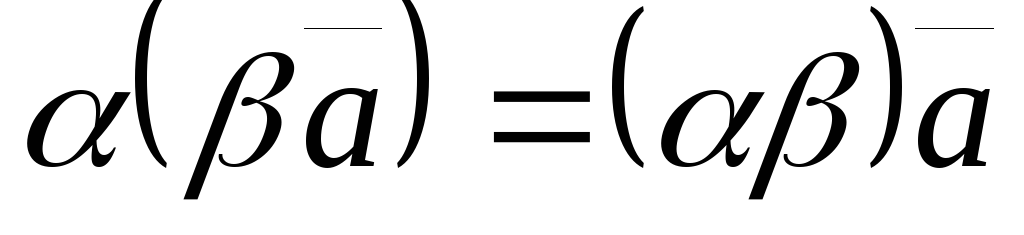 ;
; -
 .
.
Равенства 1-8
справедливы для произвольных векторов
![]() и для любых чисел
и для любых чисел
![]() .
.
Декартовы координаты. Координаты вектора. Линейные операции с векторами в координатной форме
Вспомним, как
определяются декартовы координаты
точки в пространстве:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() —
—
![]() .
.

Единичные векторы
координатных осей обозначаем
![]() или
или
![]() :
:

Координаты вектора
![]() :
:
![]() ,
,
![]() ,
,
![]() .
.
Обозначаем:
![]() ,
,
![]() и т.п.
и т.п.
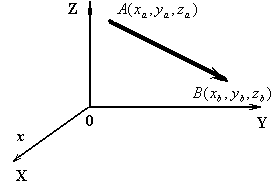
Напомним, что
координаты вектора — это ортогональные
проекции вектора на координатные оси:
если
![]() ,
то
,
то
![]() ,
,
![]() ,
,
![]() и
и
![]() .
.
Легко видеть (по
свойствам операций сложения векторов
и умножения вектора на число), что если
![]() ,
,
![]() ,
то
,
то
![]() и
и
![]() .
.
Действительно:
![]() ,
,
![]() и
и
![]() т.е.
т.е.![]() ;
;
аналогично и
![]() ,
т.е.
,
т.е.
![]() .
.
Длина вектора:
если
![]() ,
то
,
то
![]() .
.
Пример. Запись
![]() равносильна записи
равносильна записи
![]() ;
;
![]() .
.
Пример. Пусть![]() ,
,
![]() .
.
Тогда
![]() ,
,
![]() .
.
Определение.
Вектор
![]() называется радиусом-вектором точки
A:
называется радиусом-вектором точки
A:
![]() ,
,
![]()

Пространство r3 арифметических векторов
Определение.
Трехмерным арифметическим вектором
называется упорядоченная совокупность
3 чисел. Обозначается
![]() .
Числа
.
Числа
![]() называются компонентами арифметического
вектора.
называются компонентами арифметического
вектора.
Для
арифметических векторов определены
линейные операции — сложение
арифметических векторов и умножение
вектора на число: для любых
![]() и
и
![]() и
любого числа
и
любого числа
![]() —
—
![]() ,
,
Вектор
![]() называется
нулевым
вектором, а вектор
называется
нулевым
вектором, а вектор
![]() —
противоположным
вектором для вектора
—
противоположным
вектором для вектора
![]() .
.
Определение. Множество трехмерных арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов R3.
Очевидно,
что для любых
![]() ,
,
![]() ,
,
![]() из Rn
и любых
чисел α,
β справедливо:
из Rn
и любых
чисел α,
β справедливо:
-
 ,
сложение коммутативно;
,
сложение коммутативно; -
 ,сложение
ассоциативно;
,сложение
ассоциативно; -
 ;
; -
 ;
; -
 ;
;
-
 ,
умножение на число дистрибутивно
относительно сложения векторов;
,
умножение на число дистрибутивно
относительно сложения векторов; -
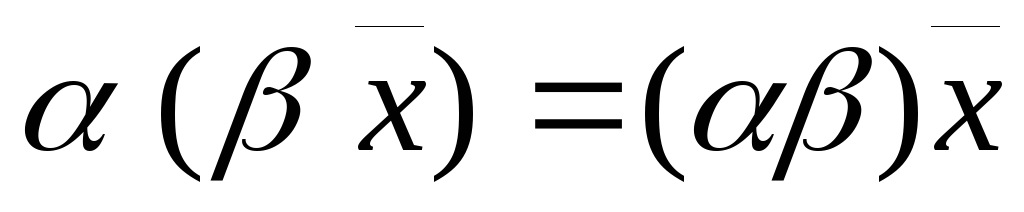 ,
умножение на число ассоциативно;
,
умножение на число ассоциативно; -
 ,
умножение вектора на число дистрибутивно
относительно сложения чисел.
,
умножение вектора на число дистрибутивно
относительно сложения чисел.
Мы видим, что операции сложения и умножения геометрических и трехмерных арифметических векторов имеют одинаковые свойства. Тогда можно проделать такое сопоставление:
Выберем
в трехмерном геометрическом пространстве
декартову систему координат. Тогда для
каждого геометрического вектора
![]() однозначно определены координаты
однозначно определены координаты
![]() :
:
![]() ,
что означает
,
что означает
![]() ,
причем, как показано выше,
,
причем, как показано выше,
![]() .
.
Это означает, что любой геометрический вектор можно рассматривать как трехмерный арифметический вектор, а пространство геометрических векторов можно изучать как пространство трехмерных арифметических векторов.
Деление отрезка в заданном отношении
Определение.
Рассмотрим отрезок AB. Говорят, что
точка M ,
принадлежащая отрезку AB делит
его в отношении
![]() ,
если
,
если
![]() .
.

![]() ,
,
![]() .
По известному свойству проекций если
.
По известному свойству проекций если
![]() ,
то
,
то
![]() ,
т.е.
,
т.е.
![]() и
и
![]() ;
аналогично
;
аналогично
![]() ,
,
![]() .
.
Точка
![]() делит отрезок
делит отрезок
![]() ,
,
![]() ,
,
![]() в отношении
в отношении
![]() .
.
В частности, точка
![]() делит отрезок
делит отрезок
![]() ,
,
![]() ,
,
![]() пополам (
пополам (![]() ).
).
Задача. Найти длину медианы треугольника ABC, проведенную из вершины A, если A(1, 0, 2), B(0,1,1), С(3, 0,-2).

Решение. Точка
M — середина BC,
![]() ,
,
![]() .
.
Тогда
![]() .
.
Ответ.
![]() .
.
Скалярное произведение векторов
Определение. Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Обозначаем:
![]() ,
,
![]() .
.

Поскольку
![]() и
и
![]() ,
то
,
то
![]()

Свойства
скалярного произведения. Нетрудно
показать, что для произвольных векторов
![]() ,
,
![]() и
и
![]() ,
и для любого числа
,
и для любого числа
![]() справедливо:
справедливо:
-
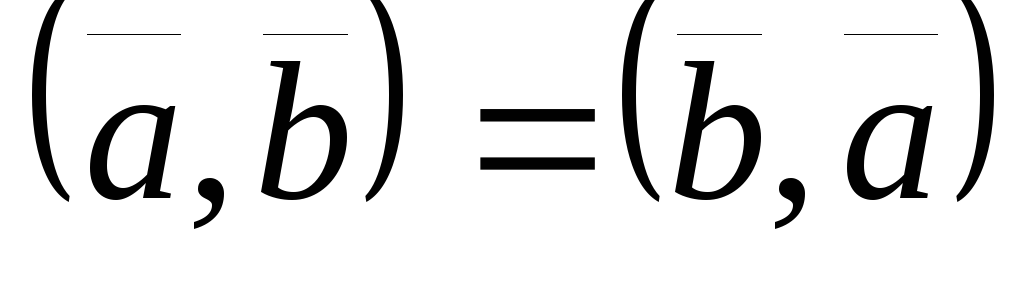 ;
; -
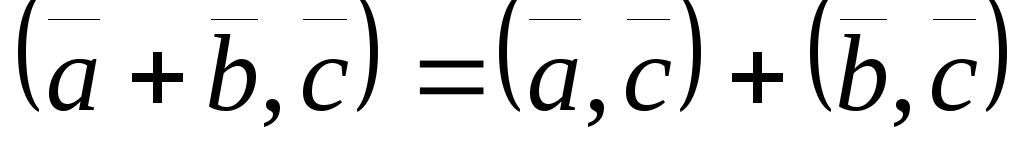 ;
; -
 ;
; -
 ,
причем
,
причем
 тогда и только тогда, когда
тогда и только тогда, когда
 .
.
Доказательства
свойств 1, 3 и 4 очевидно следуют из
определения. Докажем свойство 2:
![]() .
.
Действительно:
![]() ,
но по известному свойству проекций
,
но по известному свойству проекций
![]() ,
тогда
,
тогда
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Из свойств 1- 4 можно вывести весьма важные и полезные следствия:
-
 ;
; -
 ,
тогда и только тогда, когда векторы
,
тогда и только тогда, когда векторы
 и
и
 ортогональны (поскольку направление
нулевого вектора не определено, его
можно считать ортогональным любому
вектору);
ортогональны (поскольку направление
нулевого вектора не определено, его
можно считать ортогональным любому
вектору); -
 ;
выражение
;
выражение
 называют скалярным квадратом
вектора;
называют скалярным квадратом
вектора; -
если
 для любого вектора
для любого вектора
 ,
то вектор
,
то вектор
 — нулевой, т.е. из
— нулевой, т.е. из
 следует
следует
 ;
; -
если
 — угол между векторами
— угол между векторами
 и
и
 ,
то
,
то
 ;
; -
если векторы
 и
и
 заданы своими координатами в некоторой
декартовой системе координат:
заданы своими координатами в некоторой
декартовой системе координат:
 ,
,
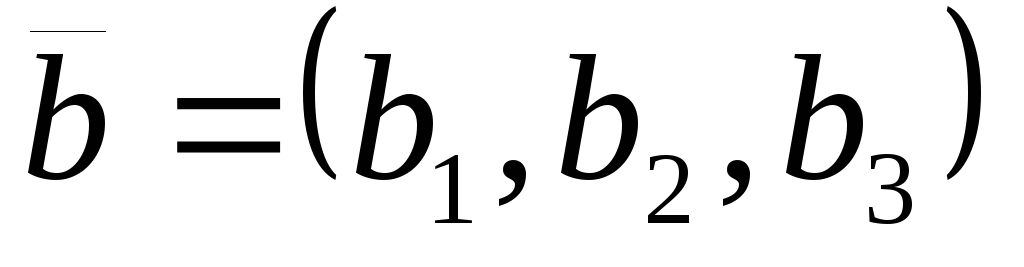 ,
то
,
то
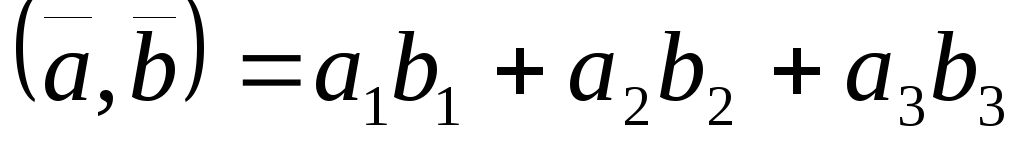 .
.
Следствия 1, 2 , 3 и 5 очевидно следуют из определения скалярного произведения. Докажем свойство 4.
Пусть
![]() для любого вектора
для любого вектора
![]() .
Значит, и для
.
Значит, и для
![]() ,
тогда
,
тогда
![]() ,
но
,
но
![]() ,
следовательно,
,
следовательно,
![]() .
.
Докажем свойство 6 — вычисление скалярного произведения в координатах.
Если векторы
![]() и
и
![]() заданы своими координатами в некоторой
декартовой системе координат:
заданы своими координатами в некоторой
декартовой системе координат:
![]() ,
,
![]() ,
то
,
то
![]() ,
,
![]() .
Вычислим
.
Вычислим
![]() :
:
![]() ,
из свойства 2 и следствия 1 следует:
,
из свойства 2 и следствия 1 следует:

из свойства 3 и следствия 2 следует:

поскольку
![]() .
.
Доказано, что
![]() .
.
Скалярное
произведение векторов можно использовать
для вычисления углов между векторами:
если
![]() — угол между векторами
— угол между векторами
![]() и
и
![]() ,
то
,
то
![]() .
.
Равенство нулю
скалярного произведения векторов —
признак ортогональности векторов:
![]() ,
тогда и только тогда, когда векторы
,
тогда и только тогда, когда векторы
![]() и
и
![]() ортогональны.
ортогональны.
Задача (Типовой
расчет!). Найти косинус угла между
векторами
![]() и
и
![]() ,
если A(1, 2, 0), B(0,
2, -1) и C(0, 0, 1).
,
если A(1, 2, 0), B(0,
2, -1) и C(0, 0, 1).
Решение.
![]() ;
;
![]() ,
,
![]() ,
,
![]() — векторы
— векторы
![]() и
и
![]() — ортогональны, угол между ними равен
— ортогональны, угол между ними равен
![]() ,
,
![]() .
.
Если не вспомнили
признак ортогональности, то можно
продолжать вычисления:
![]() ,
,
![]() ,
,
![]() .
Ответ.
.
Ответ.
![]() .
.
