Краткий конспект лекций и задачи к экзамену. / Лекции 9-10

14

Линейная алгебра и аналитическая геометрия

Краткий конспект лекций. Сливина Н.А.

Лекции 9-10

Общая теория линейных систем

Системы линейных алгебраических уравнений. Основные понятия

Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных :

Определение. Решением системы называется совокупность n значений неизвестных , при подстановке которых все уравнения системы обращаются в тождества.

Определение. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.

Напомним, что система линейных уравнений может быть записана в матричной форме:

,

где — матрица системы, — правая часть, — искомое решение,

Иногда удобно записывать систему линейных уравнений в другой матричной форме:

где — столбцы матрицы системы.

Обозначим

Матрица называется расширенной матрицей системы.

Определение. Если правая часть системы равна нулю, то система называется однородной.

Определение. Для системы однородная система (с той же матрицей системы A) называется приведенной однородной системой.

Свойства решений систем линейных алгебраических уравнений

Используя свойства линейных операций с матрицами, нетрудно доказать, справедливость следующих утверждений.

1. Если и — два решения однородной системы , то при любых действительных числах α и β вектор — решение системы .

2. Если и — два решения неоднородной системы , то вектор — решение приведенной однородной системы однородной .

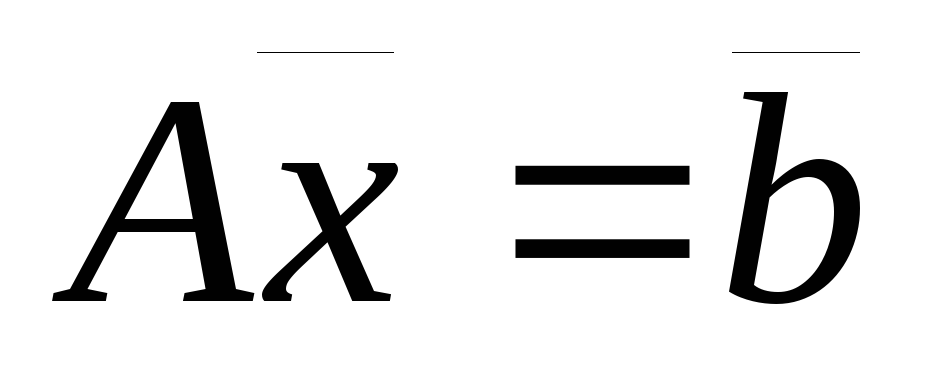3. Если решение неоднородной системы , а — решение однородной системы , то вектор — решение неоднородной системы .

Докажем, например, первое из этих свойств. Пусть и — два решения системы , т. е. и и пусть α и β любые действительные числа. Тогда , т.е. вектор — решение однородной системы.

Остальные утверждения докажите аналогично самостоятельно.

Необходимое и достаточное условие совместности системы линейных алгебраических уравнений

На вопрос о совместности системы линейных алгебраических уравнений отвечает следующая теорема.

Теорема (теорема Кронекера-Капелли). Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.

Доказательство теоремы.

Необходимость. Система совместна. Докажем, что .

Система совместна — существуют такие числа , что

т.е. вектор-столбец правой части линейно выражается через столбцы матрицы A. Это означает, что при добавлении столбца число линейно независимых столбцов не увеличивается, т.е. . Необходимость доказана.

Достаточность. . Докажем, что система совместна.

Пусть . Это означает, что среди столбцов обеих матриц есть r линейно независимых столбцов, а все остальные линейно выражаются через эти r столбцов. Не умаляя общности, положим, что линейно независимы первые r столбцов . Тогда столбцы — линейно зависимы и, следовательно, столбец линейно выражается через :.

Положим ,

тогда

т.е. вектор — решение системы ,

т.е. система совместна. Теорема доказана.

Очевидно, что однородная система всегда совместна, поскольку у нее всегда есть тривиальное — нулевое решение.

Совместность однородной системы также легко получить из теоремы Кронекера-Капелли: добавление столбца правых частей — нулевого столбца, не может увеличить ранг матрицы.

Минор матрицы. Теорема о базисном миноре

Определение. Минором матрицы порядка r называется определитель, составленный из элементов матрицы, расположенных на пересечении любых r строк и r столбцов матрицы; обозначаем M_r.

Пример.

минор M₂ расположен на пересечении 2-й и 5-й строк с 3-м и 5-м столбцами, а минор M₄ — на пересечении 1-й, 3-й, 4-й и 5-й строк с 1-м, 2-м, 4-м и 5-м столбцами.

Минор M_r, расположенный в первых r строках и в первых r столбцах матрицы , называется угловым или главным минором матрицы.

Справедлива следующая теорема.

Теорема о базисном миноре. Если ранг матрицы равен r, то у матрицы есть отличный от нуля минор порядка r. Строки и столбцы этого минора линейно независимы, а все остальные строки и столбцы матрицы через них линейно выражаются.

Доказательство теоремы опускаем. Его можно найти в учебниках, приведенных в списке литературы.

Отличный от нуля минор ­r-го порядка матрицы, ранг которой равен r, называется базисным минором, столбцы матрицы, входящие в этот минор называются базисными столбцами, а строки, входящие в базисный минор — базисными строками.

Т.е. теорема о базисном миноре утверждает, что базисные строки и базисные столбцы матрицы линейно независимы, а остальные строки и столбцы матрицы линейно выражаются через базисные.

Следствия из теоремы о базисном миноре

1. Если ранг матрицы равен r, то все миноры матрицы более высокого порядка равны нулю.

Действительно. Любой минор более высокого порядка содержит хотя бы один столбец (строку), который линейно выражается через столбцы базисного минора, и, следовательно, равен нулю, поскольку разлагается в линейную комбинацию определителей с хотя бы двумя равными столбцами:

2. Ранг матрицы равен наивысшему порядку отличных от нуля миноров матрицы.

Действительно, из теоремы о базисном миноре следует, размерность базисного минора — наибольшее число линейно независимых строк (столбцов) матрицы.

3. Строки и столбцы квадратной матрицы линейно независимы тогда и только тогда, когда ее определитель отличен от нуля.

Действительно, определитель — минор наивысшего порядка. Если он отличен от нуля, то он и есть базисный минор матрицы, т.е. все его столбцы (строки) — базисные — линейно независимые. И наоборот. Если все n строк и столбцов квадратной матрицы порядка n линейно независимы, то ранг матрицы равен n. Но по теореме о базисном миноре существует отличный от нуля минор матрицы порядка n, а такой минор — определитель матрицы.

Замечание. Утверждение теоремы о базисном миноре легко понять на примере ступенчатой матрицы. Вспомним, что ранг ступенчатой матрицы

равен числу r ненулевых строк. Видно, что главный минор этой матрицы, M_r отличен от нуля:

ведь все диагональные элементы отличны от нуля.

Любой минор более высокого порядка содержит нулевую строку, т.е. равен нулю.

Нетривиальная совместность однородных систем. Необходимое и достаточное условие нетривиальной совместности однородной системы

Мы уже говорили, что однородная система линейных алгебраических уравнений всегда совместна. Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди этих решений есть и ненулевые и в этом случае система называется нетривиально совместной.

Пример. Вектор — отличное от нуля решение однородной системы

Теорема (необходимое и достаточное условие нетривиальной совместности однородной системы). Для того чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных.

Доказательство теоремы

Необходимость. Система нетривиально совместна. Это означает, что существуют числа не все равные нулю, для которых справедливо . Последнее равенство означает, что n столбцов матрицы систем линейно зависимы и, следовательно, ранг матрицы системы (максимальное число линейно независимых столбцов) меньше числа столбцов, меньше числа неизвестных. Необходимость доказана.

Достаточность. Пусть ранг r матрицы системы меньше числа n неизвестных. По теореме о базисном миноре из этого следует, что существует отличный от нуля минор матрицы порядка r. Не умаляя общности, будем полагать, что базисный минор — главный минор матрицы

Рассмотрим первые r уравнений системы (по теореме о базисном миноре остальные уравнения — линейные комбинации этих первых уравнений):

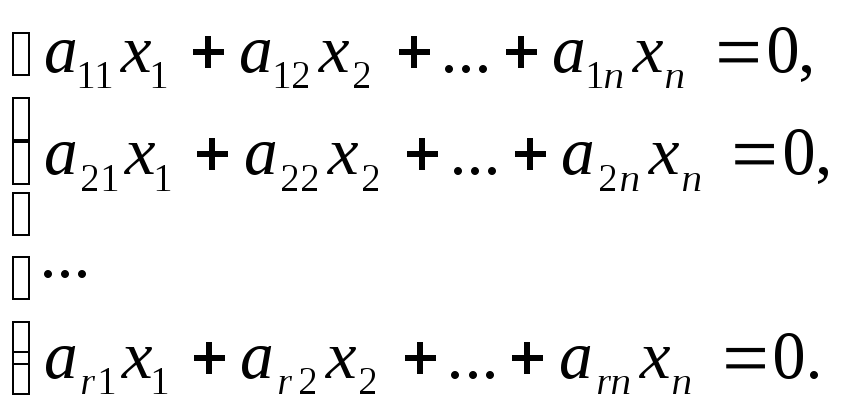
Оставим слева первые r неизвестных, а остальные n-r неизвестные перенесем вправо и получим неоднородную систему линейных уравнений относительно неизвестных :

Определитель полученной системы — отличный от нуля базисный минор M_r.

Уравнения системы справедливы при произвольных значениях переменных Их естественно называть свободными. А переменные в левой части уравнений системы естественно назвать базисными.

Базисные переменные можно вычислить по формулам Крамера , i = 1, 2, …, r . Здесь — определитель матрицы системы, а — определитель, полученный из M_r заменой i-го столбцом правых частей. Вычислим, например, x₁.

Здесь — некоторые числа.

Итак, . Аналогично — т.е. базисные переменные линейно выражаются через свободные переменные.

Положим, например такие значения свободных переменных:

Тогда вектор — отличное от тождественного нуля решение однородной системы . Т.е. однородная система нетривиально совместна. Теорема доказана.

Фундаментальная система решений однородной системы. Структура общего решения однородной системы

Вспомним, что решения однородной системы — векторы из Rⁿ. Вспомним также, что в силу свойств решений линейной однородной системы множество L ее решений — линейное подпространство в Rⁿ. Действительно: если и — два решения однородной системы , то при любых действительных числах α и β вектор — решение системы , иначе говоря, для любых и и любого числах α и . Доказано также, что если ранг r матрицы системы меньше числа неизвестных n, то система имеет ненулевые решения.

Определение. Выражение, позволяющее вычислить все (любое) решения системы, называется общим решением системы.

В теореме о нетривиальной совместности однородной системы показано, что если r — ранг матрицы системы, то r базисных переменных выражаются через свободные переменные по формулам

, .

Здесь для простоты полагали, что базисные переменные — это первые r переменных. Вообще говоря, это могут быть любые r переменных.

Итак, , — т.е. базисные переменные линейно выражаются через свободные переменные.

Построим n-r ненулевых решений однородной системы специальным образом.

Сначала положим и полученное решение обозначим .

Затем положим и полученное решение обозначим ,

и т.д., и, наконец, положим и полученное решение обозначим . Имеем (см. док-во теоремы о нетривиальной совместности)

.

Нетрудно видеть, что эти n-r ненулевые решения линейно независимы.

Действительно, запишем матрицу, столбцами которой являются векторы :

.

Минор этой матрицы, расположенный в последних n-r строках равен 1, отличен от нуля. Это означает, что ранг матрицы равен n-r и что ее n-r столбца линейно независимы. А столбцы этой матрицы — ненулевые решения однородной системы .

С другой стороны, любое решение системы, в соответствии с приведенными выше формулами, можно записать в виде:

Здесь произвольные значения свободных переменных обозначены буквами .

Подведем итог:

• построена система , состоящая из n-r линейно независимых решений однородной системы;

• любое решение системы линейно выражается через решения ;

• множество решений однородной системы — линейное подпространство.

Тогда можно утверждать:

1. размерность подпространства L решений однородной системы равна n­­­ – r , где n — число неизвестных, r = RgA: dimL = n – r;

2. система — базис в подпространстве L решений однородной системы ;

3. выражение — общее решение однородной системы.

Определение. Система , состоящая из n-r линейно независимых решений однородной системы , , RgA=r , называется фундаментальной системой решений однородной системы.

Выше мы доказали следующие утверждения.

Утверждение. Фундаментальная система решений однородной системы — базис пространства решений однородной системы.

Теорема о структуре общего решения однородной системы линейных алгебраических уравнений. Если ранг r матрицы однородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде линейной комбинации решений фундаментальной системы: .

Пример 1. Исследуем однородную систему линейных алгебраических уравнений

Исследовать однородную систему — ответить на вопрос является ли система нетривиально совместной, и если является, то найти ее общее решение.

Решение. Решим задачу методом Гаусса-Жордана.

Приведем матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

Ранг матрицы системы равен r = 2, число неизвестных n =4, r < n — система нетривиально совместна. Кроме того, очевидно, множества решений исходной системы и системы с преобразованной матрицей совпадают.

Продолжим преобразование матрицы системы, выполняя элементарные операции со строками так, чтобы базисный минор матрицы стал единичным (обратный ход метода Гаусса):

.

Запишем эквивалентную систему уравнений:

Главный минор матрицы этой системы — .

Следовательно, переменные — базисные переменные, а — свободные.

Перенесем свободные переменные вправо:

Получили выражение базисных переменных через свободные. Такое выражение — общее решение однородной системы, записанное «на языке систем».

Найдем базис в подпространстве решений системы (фундаментальную систему). Для этого положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор — решение однородной системы.

Затем положим значения свободных переменных равными и вычислим базисные переменные:

Тогда вектор — решение однородной системы.

Векторы — линейно независимые решения однородной системы размерность пространства решений которой d = n– r = 4 – 2 = 2, т.е. — базис пространства решений.

Запишем общее решение системы:

.

Проверим:

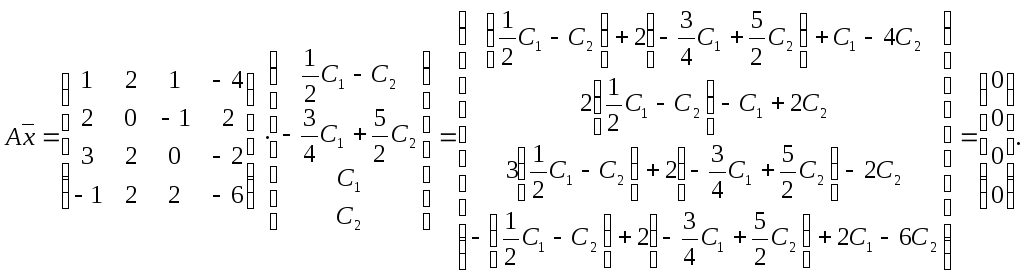
Верно.

Ответ: Общее решение системы , — произвольные постоянные. Базис в пространстве решений системы — , .

Структура общего решения неоднородной системы

Вспомним одно из свойств решений линейной неоднородной системы:

Если и — два решения системы , то вектор — решение приведенной однородной системы .

Поскольку выражение задает все решения однородной системы, то для любых двух решений и неоднородной системы справедливо

и, следовательно, выражение позволяет вычислить любое решение неоднородной системы.

Таким образом доказана теорема о структуре общего решения линейной неоднородной системы.

Теорема о структуре общего решения неоднородной системы линейных алгебраических уравнений. Если ранг r матрицы неоднородной системы линейных уравнений меньше числа неизвестных n, то общее решение системы можно записать в виде

где — произвольные константы, а — фундаментальная система решений приведенной однородной системы, — некоторое известное (частное) решение неоднородной системы.

Пример 2. Исследуем неоднородную систему линейных алгебраических уравнений

Исследовать неоднородную систему — ответить на вопрос является ли система совместной, и если является, то найти ее общее решение.

Решение. Решим задачу методом Гаусса-Жордана.

Приведем расширенную матрицу системы к ступенчатому виду, выполняя элементарные преобразования строк (прямой ход метода Гаусса):

Ранг расширенной матрицы системы равен рангу матрицы системы и равен двум:

RgA_p =RgA= r = 2, система совместна. Число неизвестных n =4, r < n — приведенная однородная система нетривиально совместна.