Краткий конспект лекций и задачи к экзамену. / Лекция 6

Линейная алгебра и аналитическая геометрия

Краткий конспект лекций. Сливина Н.А.

Лекция 6. МАТРИЦЫ

Матрицы. Основные понятия. Виды матриц. Равенство матриц

Вспомним определения и обозначения из предыдущей лекции.

Прямоугольная таблица m·n чисел, расположенных в m строках и n столбцах называется прямоугольной (m,n) матрицей или просто матрицей.

Будем обозначать матрицы заглавными буквами — A, элементы матриц — , столбцы матрицы — , а строки — , транспонированная матрица — .

Некоторые часто встречающиеся виды матриц имеют собственные названия:

квадратная матрица, , матрица, у которой одинаковое число строк и столбцов;

матрица-строка,, матрица, у которой одна строка;

матрица-столбец, , матрица, у которой один столбец;

диагональная матрица, квадратная матрица, у которой все внедиагональные элементы раны нулю;

единичная матрица, диагональная матрица, у которой все диагональные элементы — единицы нулю;

нулевая матрица, , матрица, все элементы которой — нули;

верхняя треугольная матрица, 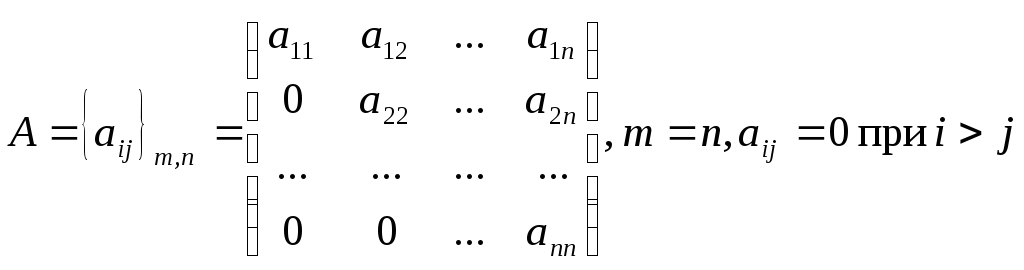, квадратная матрица, у которой все элементы, расположенные ниже диагонали — нули;

нижняя треугольная матрица, , квадратная матрица, у которой все элементы, расположенные выше диагонали — нули.

В дальнейшем важную роль будет играть ступенчатая матрица: ,

т.е. существует такое число r, , что для всех , и для всех при . Важно понимать, то у ступенчатой матрицы первые r диагональных элементов отличны от нуля:.

Пример. Ступенчатые матрицы:

Определение. Две матрицы называются равными, если они имеют одинаковую размерность и равные соответственные элементы:

Линейные операции с матрицами. Линейными операциями называются операции сложения и умножения на число.

Определение. Суммой двух матриц одинаковой размерности называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых: .

Определение. Произведением матрицы на число называется матрица той же размерности, каждый элемент которой равен произведению соответствующего элемента на число: .

Для операций сложения и умножения матрицы на число справедливо:

1. A+B = B+A,

2. A+(B+C) = (A+B)+C,

3. α(A+B) = αA+αB,

4. α(βA) = (αβ)A,

5. (α+β)A=αA+βA,

6. 1·A=A,

7. 0·A= .

Здесь A, B, C — произвольные матрицы одинаковой размерности, — нулевая матрица той же размерности (читается «тэта»), и — произвольные числа.

Умножение матриц

Операция умножения матрицы на матрицу определяется более сложным образом.

Определение. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если

то произведением матриц A и B называется матрица

, элементы которой вычисляются по формуле

, ; произведение матриц A и B обозначается AB: C=AB.

Пример.

.

Для произведения матриц соответствующих порядков справедливо:

1. A·B ≠ B·A,

2. (A + B) · C = A·C + B·C,

3. C·(A + B) = C·A + C·B,

4. α(A·B) = (αA) ·B,

5. (A·B) ·C = A·(B·C),

6. (AB)^T = B ^TA ^T,

7. , A, B — квадратные матрицы одинаковой размерности.

8. AE=EA=A, A— квадратная матрица, E — единичная матрица соответствующей размерности.

Если AB = BA, то матрицы A и B называются перестановочными.

Непосредственным вычислением легко проверить основное свойство единичной матрицы

Обратная матрица

Определение. Если существует квадратная матрица X той же размерности, что и матрица A, удовлетворяющая соотношениям A·X=X·A=E, то матрица A называется обратимой, а матрица X называется обратной к матрице A и обозначается A_­­^-1.

Здесь E — единичная матрица соответствующей размерности.Т.е. A·A_­­^-1= A_­­^-1·A=E.

Пример.

Теорема о существовании обратной матрицы. Если , то матрицаA обратима и

.

Здесь — алгебраическое дополнение элемента матрицы A.

Доказательство теоремы. Докажем, что для матрицы (транспонировали матрицу из алгебраических дополнений) справедливо:.

Вычислим .

Если , то — сумма произведений элементов i-й строки матрицы A на их алгебраические дополнения. Если же Если , то — сумма произведений элементов i-й строки матрицы A на алгебраические дополнения другой ( j-й строки, ). Отсюда следует, что диагональные () элементы матрицы равны единице, а внедиагональные () — равны нулю, т.е. .

Равенство доказывается совершенно аналогично. Докажите самостоятельно.

Теорема (необходимое и достаточное условие существования обратной матрицы).

Для того, чтобы матрица A была обратима, необходимо и достаточно, чтобы .

Доказательство теоремы. Необходимость. Дано: матрица A обратима. Докажем, что . Действительно, поскольку A — обратима, то и , и, следовательно, . Отсюда, в частности, следует, что окажем, что .

Достаточность. Дано: . Но тогда обратимость матрицы A следует из теоремы о существовании обратной матрицы. Теорема доказана.

Теорема о единственности обратной матрицы. Обратная матрица единственна.

Доказательство. Докажем «от противного». Пусть это не так, и пусть и , . Из определения обратной матрицы следует: , .

Тогда из ассоциативности умножения матриц и свойств единичной матрицы следует: Выполним некоторые вычисления: , т.е. . Противоречие с предположением доказывает утверждение теоремы.

Аналогичными вычислениями можно доказать следующие свойства обратной матрицы:

1. .

2. .

Действительно:

, и

совершенно аналогично, , т.е. .

.

Нетрудно также доказать, что матрица, обратная к диагональной матрице — диагональная, обратная к треугольной — треугольная, обратная к симметричной матрице — симметрична. Докажите эти утверждения самостоятельно.

Ниже приведен порядок операций при вычислении обратной матрицы.

Пример. Вычислим :;

составим матрицу из алгебраических дополнений:

,

,

,

; транспонируем полученную матрицу: ;

разделив каждый элемент последней матрицы на , получим обратную матрицу:

Проверим:

Матричная запись системы линейных алгебраических уравнений. Рассмотрим систему линейных алгебраических уравнений

Обозначим: , , ,

A — матрица системы, B — правая часть, X — матрица-столбец неизвестных.

Тогда:

тогда и только тогда, когда для элементов матрицы X справедливы равенства рассмотренной системы. Т.е. система эквивалентна матричному уравнению A·X = B, в том смысле, что если числа являются решением рассмотренной системы, то соответствующая матрица X является решением матричного уравнения; и наоборот, если матрица X является решением матричного уравнения, то ее элементы являются решением рассмотренной системы.

Матричные уравнения. Рассмотрим матричное уравнение A·X = B.

Если m=n и матрица A обратима, то

,

т.е. получили выражение для решения системы матричного уравнения

A·X = B. Ясно, что по этой формуле можно вычислить решение системы n линейных алгебраических уравнений относительно n неизвестных (см. запись системы в матричной форме).

Аналогично, если соответствующие матрицы обратимы, имеем:

X·A = B, X = B·A^-1,

A·X·B = C, X = A^-1·C· B^-1,

A·X+B = 0, A·X = - B, X = - A^-1·B.

Пример. Решим матричное уравнение :

.

Проверим:

Формулы Крамера. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных

Обозначим: — определитель матрицы системы, и — определитель матрицы, полученной из матрицы системы заменой j-го столбца столбцом правых частей.

Если определитель матрицы системы отличен от нуля, , то решение системы

определяется равенствами: .

Докажем это утверждение. Пусть.

Обозначим и покажем, что Вычислим

Вычислим определитель разложением по первому столбцу, определитель — по второму, …, — по n-му:

, поскольку определитель отличается от только j-м столбцом.

Тогда

поскольку

Т.е. Формулы Крамера доказаны.

Замечание. Нетрудно, показать, что выражения и — две формы записи одного и того же равенства.

Действительно,

Пример. Решим по формулам Крамера систему:

, , ,

, , ,

Проверим:

Элементарные преобразования матриц

Помимо операций с матрицами определены операции с элементами матриц, операции со столбцами и строками матрицы — так называемые элементарные преобразования матриц.

Определение. Элементарными преобразованиями матрицы называют следующие операции:

1. перестановка любых двух строк (столбцов) матрицы;

2. умножение любой строки (столбца) на произвольное, отличное от нуля, число;

3. сложение любой строки (столбца) с другой строкой (столбцом), умноженной (умноженным) на произвольное, отличное от нуля, число.

4. к элементарным преобразованиям иногда относят и операцию транспонирования матрицы.

Приведение матрицы к ступенчатому виду Гауссовым исключением

Утверждение. Любую прямоугольную матрицу можно с помощью элементарных преобразований привести к ступенчатой форме.

Это утверждение на лекции доказано.

Пример. Приведем к ступенчатой форме матрицу .

Алгоритм приведения матрицы к ступенчатой форме с помощью элементарных преобразований называют Гауссовым исключением или методом Гаусса.