Краткий конспект лекций и задачи к экзамену. / Лекция 13

6

Линейная алгебра и аналитическая геометрия

Краткий конспект лекций. Сливина Н.А.

Лекция 13

Собственные значения и собственные векторы линейного оператора

Определение собственного значения и собственного вектора линейного оператора

Определение. Пусть A — линейный оператор, действующий в линейном пространстве Rⁿ. Число называется собственным значением, а ненулевой вектор из Rⁿ — соответствующим собственным вектором линейного оператора A, если они связаны между собой соотношением..

Примеры.

1. Нулевой оператор: , т.е. — собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

2. Тождественный (единичный) оператор I: — т.е. собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

3. Оператор P₂ — оператор проектирования пространства R³ на подпространство R² параллельно вектору : , , т.е. — собственное значение оператора, проектирования, а соответствующие собственные векторы — все ненулевые векторы R³, третья координата которых равна нулю: .

Пусть A— матрица оператора в некотором базисе в Rⁿ.

Собственные значения оператора и соответствующие им собственные векторы связаны соотношением или, что то же самое, :

, . Здесь — единичный оператор.

По теореме о связи координат образа и прообраза имеем: , где E — единичная матрица, а — нулевой вектор Rⁿ .

Это означает, что собственный вектор оператора является ненулевым решением линейной однородной системы . Ненулевое решение однородной системы (система нетривиально совместна), существует тогда и только тогда, когда определитель матрицы системы равен нулю: . Следовательно, собственные значения линейного оператора могут быть вычислены как корни уравнения , а собственные векторы — как решения соответствующих однородных систем.

Легко видеть, что определитель — многочлен n-й степени относительно .

Определение. Уравнение называется характеристическим уравнением оператора, а многочлен — характеристическим многочленом оператора.

Примеры.

1. Нулевой оператор: , матрица нулевого оператора — нулевая матрица соответствующего порядка, т.е. т.е. — единственное собственное значение нулевого оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

2. Тождественный (единичный) оператор I: матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. т.е. — единственное собственное значение тождественного оператора, а соответствующие собственные векторы — все ненулевые векторы пространства Rⁿ.

3. Оператор P₂ — оператор проектирования пространства R³ на подпространство R² параллельно вектору : , тогда матрица тождественного оператора — единичная матрица соответствующего порядка, т.е. т.е. и — собственные значения оператора.

Найдем соответствующие собственные векторы.

Пусть , тогда соответствующие собственные векторы — ненулевые решения системы т.е.

т.е. вектор

— собственный вектор оператора, отвечающий собственному значению и, следовательно, все векторы вида — собственные векторы оператора, отвечающие собственному значению .

Теперь положим , тогда соответствующие собственные векторы — ненулевые решения системы т.е.

т.е. векторы

— линейно независимые векторы, которые являются собственными векторами оператора, отвечающими собственному значению и, следовательно, все векторы вида 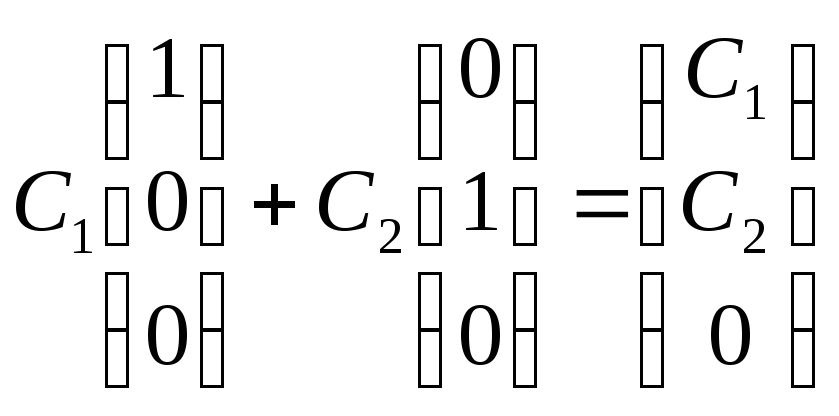— собственные векторы оператора, отвечающие собственному значению .

4. . Оператор U_ поворота пространства R² на угол φ относительно начала координат против часовой стрелки:

.

Матрица оператора , тогда

Характеристическое уравнение имеет единственный корень при и при ,. Если , , и т.е. соответствующие собственные векторы — все ненулевые векторы пространства R².

При — оператор поворота не имеет собственных векторов.

И, наконец, при и , , оператор поворота совпадает с тождественным оператором, собственные значения и собственные векторы которого вычислены выше.

Однако, все приведенные выше рассуждения относились к матрице оператора, записанной в некотором определенном базисе в пространстве Rⁿ. А поскольку в пространстве Rⁿ существует много различных базисов, то может возникнуть впечатление, что собственные значения зависят от выбранного базиса. Докажем, что это не так.

Пусть и — два базиса в Rⁿ, а — матрица перехода от базиса к базису , т.е. . Тогда

т.е. характеристическое уравнение инвариантно, не зависит от базиса и его корни — собственные значения оператора — не зависят от базиса.

Пример (ТР Линейная алгебра, задача 9). Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей .

Решение. Запишем характеристическое уравнение:

, , , .

Собственные значения оператора , .

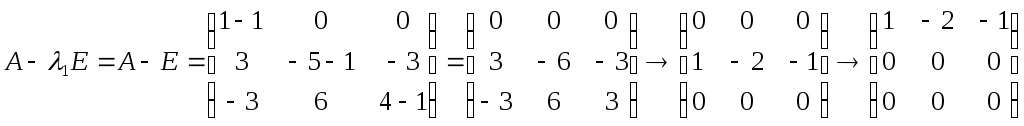
Найдем собственный вектор, отвечающий собственному значению :

, , ,

, , ,

, — собственному значению отвечают два линейно независимых собственных вектора и .

Найдем собственный вектор, отвечающий собственному значению :

, , ,

, — собственному значению отвечает собственный вектор .

Проверим. , , . Верно.

Ответ: собственные значения оператора: , ; соответствующие собственные векторы: , ,.

Свойства собственных векторов

Для собственных значений и собственных векторов линейного оператора справедливы следующие утверждения:

1. характеристический многочлен оператора, действующего в Rⁿ является многочленом n-й степени относительно ;

2. линейный оператор, действующий в Rⁿ, имеет не более n различных собственных значений;

3. собственные векторы оператора определяются с точностью до постоянного сомножителя; поэтому принять вычислять собственные векторы единичной длины — орты собственных векторов;

докажем, что если — собственный вектор линейного оператора A, отвечающий собственному значению , то для любого отличного от нуля числа вектор ()— собственный вектор оператора A, отвечающий собственному значению : ;

4. корни характеристического многочлена не зависят от базиса;

5. собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Докажем линейную независимость собственных векторов, отвечающих различным собственным значениям.

Пусть — собственный вектор линейного оператора A, отвечающий собственному значению , а — собственный вектор линейного оператора A, отвечающий собственному значению , : и .

Предположим, что векторы и линейно зависимы. Это означает, что один из них линейно выражается через другой: существует такое число , что . Тогда:

.

Собственный базис линейного оператора. Матрица линейного оператора в собственном базисе

Если линейный оператор, действующий в Rⁿ, имеет n различных собственных значений, то собственные векторы оператора образуют базис в Rⁿ.

Действительно, ведь мы доказали, что они линейно независимы.

Определение. Базис, составленный из собственных векторов линейного оператора называют собственным базисом оператора.

Если — собственный базис оператора A, то, поскольку то матрица оператора в этом базисе — диагональная матрица с собственными значениями на диагонали.

Пример. Найти матрицу оператора из предыдущего примера в собственном базисе. Оператор в предыдущем примере задан в некотором базисе матрицей .

Решение. В предыдущем примере найдены собственные значения

, и соответствующие собственные векторы оператора —

, , .

Собственные векторы оператора образуют базис в R³. Далее.

Первый способ

Поскольку в базисе

, , и .

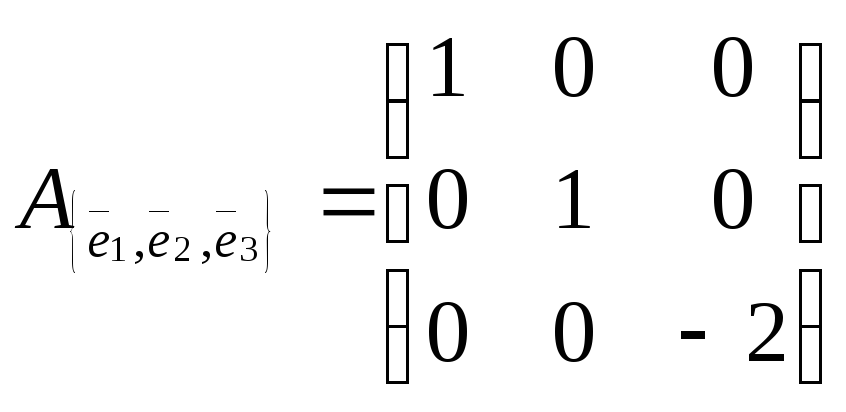Второй способ

Запишем матрицу перехода от исходного базиса — к собственному базису : . Тогда .

Решения, полученные обоими способами совпали.

Ответ: , , , .