
Краткий конспект лекций и задачи к экзамену. / Задачи к экзамену ЛинАл
.doc
СТАНДАРТ
ЛИНЕЙНАЯ АЛГЕБРА
Задачи к экзамену
Составили Сливина Н.А.
ВЕКТОРНАЯ АЛГЕБРА
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,1,0), C(1, 1, 1). Найти координаты векторов
 .
Изобразить эти векторы.
.
Изобразить эти векторы. -
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,1,0), C(1, 1, 1). Найти длины сторон треугольника.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,1,0), C(1, 1, 1). B1C1 — средняя линия треугольника ABC, параллельная стороне BC. Найти длину B1C1.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,2,0), C(1, 2, 1). Найти внутренние углы треугольника ABC.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,1,0), C(1, 1, 1). Вычислить площадь треугольника.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,2,0), C(1, 2, 3). Найти длину медианы, проведенной из вершины A.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,2,0), C(1, 2, 3). Найти длину высоты, опущенной на строну AB.
-
Треугольник ABC задан координатами вершин: A(1, 0, 0), B(0,2,0), C(1, 2, 3). Найти длину высоты, опущенной на строну AB.
-
Вычислить объем тетраэдра OABC, O(0, 0, 0), A(1, 0, 0), B(0,1,0), C(1, 1, 1). Изобразить тетраэдр.
-
Вычислить объем тетраэдра OABC, O(0, 0, 0), A(1, 0, 0), B(0,1,0), C(0, 0, 1). Изобразить тетраэдр.
-
Записать координаты какого-либо вектора, ортогонального вектору
 .
. -
Записать координаты какого-либо вектора, коллинеарного вектору
 .
. -
Записать координаты какого-либо вектора, компланарного векторам
 .
. -
Записать координаты какого-либо вектора, компланарного векторам
 .
. -
Записать координаты какого-либо вектора, образующего острый угол с вектором
 .
. -
Записать координаты какого-либо вектора, образующего тупой угол с вектором
 .
. -
Записать координаты какого-либо вектора, образующего с векторами
 левую тройку.
левую тройку. -
Доказать, что вектор
 ортогонален вектору
ортогонален вектору
 .
. -
Вычислить векторное произведение векторов
 и
и
 .
. -
Вычислить смешанное произведение

-
Дано:
 ,
,
 ,
,
 .
Вычислить:
.
Вычислить:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ
-
Записать уравнения координатных плоскостей.
-
Записать параметрические уравнения координатных осей.
-
Записать канонические уравнения координатных осей.
-
Записать уравнения граней тетраэдра OABC, где O(0, 0, 0), A(1, 0, 0), B(0,1,0), C(1, 1, 1).
-
Записать уравнения высоты тетраэдра OABC, опущенной из вершины O. Здесь O(0, 0, 0), A(1, 0, 0), B(0,1,0), C(1, 1, 1).
-
Записать уравнение плоскости, проходящей через вершину O(0, 0, 0) тетраэдра OABC и перпендикулярной основанию ABC. Здесь A(1, 0, 0), B(0,1,0), C(1, 1, 1).
-
Записать уравнения прямой, проходящей через вершину A(1, 0, 0) тетраэдра OABC перпендикулярно его основанию ABC. Здесь O(0, 0, 0), B(0,1,0), C(1, 1, 1).
-
Записать уравнения граней призмы OABO1A1B1, где O(0, 0, 0), A(1, 0, 0), B(0,1,0), O1 (0, 0, 1), A1 (1, 0, 1), B1 (0,1,1).
-
Записать уравнения ребер призмы OABO1A1B1, где O(0, 0, 0), A(1, 0, 0), B(0,1,0), O1 (0, 0, 1), A1 (1, 0, 1), B1 (0,1,1).
-
Найти расстояние между ребрами BC и OO1 призмы OABCO1A1B1C1,
где O(0, 0, 0), A(1, 0, 0), B(1,2,0), С(0,3,0), O1 (0, 0, 1), A1 (1, 0, 1), B1 (1,2,1), C1 (0, 3, 1).
ОПРЕДЕЛИТЕЛИ
-
Решить уравнения: a)
 ;
б)
;
б)
 ;
в)
;
в)
 .
. -
Вычислить определители:
a)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
 ;
ж)
;
ж)
 ;
з)
;
з)
 .
.
-
Вычислить определители, приведением к диагональной форме:
a)
 ;
б)
;
б)
 .
.
-
Как изменится определитель 3-го порядка, если знаки всех его элементов поменять на противоположные?
-
Как изменится определитель третьего порядка, если все его строки записать в обратном порядке? Сравните
 и
и
 .
. -
Как изменится определитель четвертого порядка, если все его строки записать в обратном порядке? Сравните
 и
и
 .
.
МАТРИЦЫ
-
Вычислить:
а)
 ;
б)
;
б)
 ;
;
в)
 ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
 ж)
ж)
 ;
;
з)
 .
.
-
Вычислить обратную матрицу, проверить умножением:
а)
![]() ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
;
д)
 ;
е)
;
е)
 ;
ж)
;
ж)
 .
.
ПРОСТРАНСТВО АРИФМЕТИЧЕСКИХ ВЕКТОРОВ Rn
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В Rn
-
Векторы
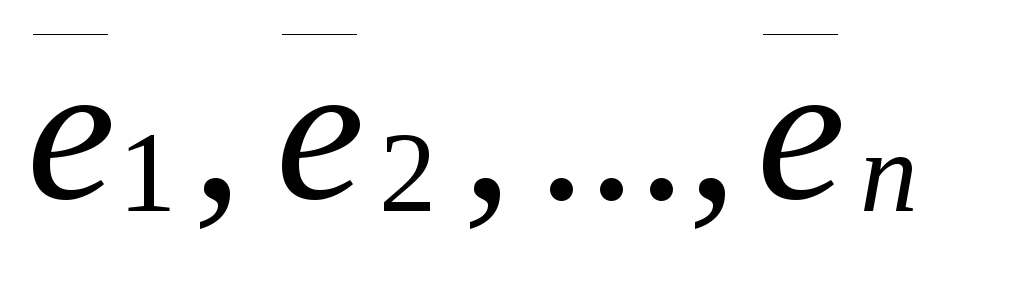 заданы своими координатами в некотором
базисе. Доказать, что они образуют базис
в соответствующем пространстве Rn:
заданы своими координатами в некотором
базисе. Доказать, что они образуют базис
в соответствующем пространстве Rn:
а)
![]() ;
;
б)
![]() .
.
-
Исследовать на линейную зависимость систему векторов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
.
-
Доказать, что множество векторов пространства R6, компоненты которых с четными номерами равны нулю, образуют линейное подпространство в R6. Найти базис и размерность этого подпространства.
-
Доказать, что множество векторов пространства R4, первая и последняя компоненты которых равны нулю, образуют линейное подпространство в R4. Найти базис и размерность этого подпространства.
-
Привести матрицу к ступенчатому виду, указать ее ранг, указать размерность пространства строк и размерность пространства столбцов этих матриц:
а)
 ;
б)
;
б) ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 .
.
-
Пусть
 — произвольные
векторы из R2.
Показать, что скалярное произведение
в R2
можно определить
равенствами:
— произвольные
векторы из R2.
Показать, что скалярное произведение
в R2
можно определить
равенствами:
а)
![]() ;
б)
;
б)
![]() .
.
-
Вычислить скалярное произведение, длины и угол между векторами
 и
и
 в естественном
(стандартном) базисе. Вычислить скалярное
произведения этих векторов, их длины,
угол между ними, используя скалярное
произведение, определенное равенством
в естественном
(стандартном) базисе. Вычислить скалярное
произведения этих векторов, их длины,
угол между ними, используя скалярное
произведение, определенное равенством
 ,
где
,
где
 ,
,
 — произвольные
векторы из R2.
Сравните результаты вычислений.
— произвольные
векторы из R2.
Сравните результаты вычислений. -
Вычислить скалярное произведение, длины и угол между векторами
 и
и
 в естественном
(стандартном) базисе. Вычислить скалярное
произведения этих векторов, их длины,
угол между ними, используя скалярное
произведение, определенное равенством
в естественном
(стандартном) базисе. Вычислить скалярное
произведения этих векторов, их длины,
угол между ними, используя скалярное
произведение, определенное равенством
 ,
где
,
где
 ,
,
 — произвольные
векторы из R2.
Сравните результаты вычислений.
— произвольные
векторы из R2.
Сравните результаты вычислений. -
Доказать ортогональность системы векторов; дополнить систему до ортогонального базиса:
а)
![]() ;
б)
;
б)
![]() .
.
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
-
Решить системы линейных алгебраических уравнений по формулам Крамера:
а)
 б)
б)
 в)
в)

-
Решить системы линейных алгебраических уравнений как матричные уравнения:
а)
 б)
б)
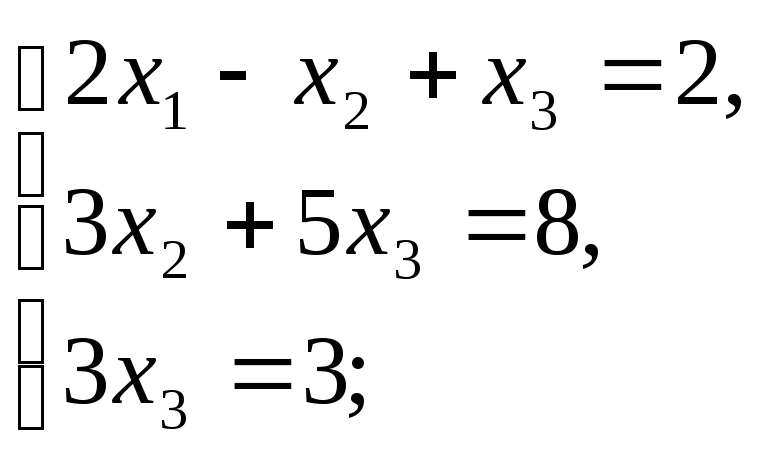 в)
в)

-
Исследовать системы линейных алгебраических уравнений (доказать совместность, записать фундаментальную систему решений, найти и проверить общее решение):
а)
 б)
б)
 в)
в)

г)
 д)
д)

ЛИНЕЙНЫЙ ОПЕРАТОР МАТРИЦА ЛИНЕЙНОГО ОПЕРАТОРА
-
Линейные операторы A и B, действующие в R3, заданы матрицами
 ,
,
 .
Найти матрицы операторов:
.
Найти матрицы операторов:
а) AB; б) A2+ B; г) A+ BA.
-
Линейный оператор A, действующий в R3, задан матрицей
 .
Найти координаты образа
.
Найти координаты образа
 вектора
вектора
 .
. -
Линейные операторы, действующие в R3, заданы своими матрицами. Найти собственные значения и собственные векторы операторов:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
-
Линейные операторы, действующие в R3, заданы своими матрицами. Найти матрицы операторов в указанных базисах:
а)
![]() ,
,
![]() б)
б)
![]() ,
,
![]()
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Определить вид поверхности. Изобразить ее схематически. Найти и изобразить линии пересечения поверхности с координатными плоскостями и с заданной плоскостью.
-
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
. -
 ,
,
 .
.
