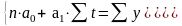4. Методы выявления тенденции развития в рядах динамики

Для характеристики показателей ряда динамики применяют методы, которые позволяют осуществить прогноз, найти недостающие компоненты ряда. Используя показатель среднего темпа роста и последний показатель ряда динамики, осуществляют прогноз на будущее (экстраполируют ряд динамики).

Тренд – это основная (достаточно устойчивая) тенденция развития явления в ряду динамики.

Методы:

Ретрополяция - нахождение по имеющимся данным за определенный период времени недостающих значений в начале динамического ряда.

Интерполяция - расчет по имеющимся данным за определенный период времени некоторых недостающих значений внутри этого периода.

Экстраполяция- расчет прогнозного значения.

Пример 2. По имеющимся данным о денежной массе необходимо определить ее прогнозное значение на 01.10.2008г. и 01.11.2008г.

Дата	Денежная масса (М2), млрд. руб.
01.06.2008	6 693,1
01.07.2008	7 092,3
01.08.2008	7 230,7
01.09.2008	7 449,3

Для расчета прогнозных значений необходимо определить средний темп (коэффициент) роста за рассматриваемый период:

• 

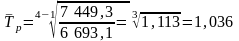
• По цепным темпам роста

; ;

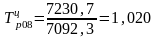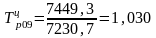
Прогнозное значение на октябрь составит

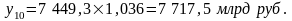
Прогнозное значение на ноябрь составит

Все факторы, влияющие на уровень ряда подразделяют на 3 группы:

1. тренд;

2. сезонные колебания;

3. случайные отклонения.

Для выявления тренда используют методы механического и аналитического выравнивания.

Механическое выравнивание:

1. Графический

Строят кривую. Если на рисунке тенденция строго не проявляется, то применяют более сложные методы выявления тренда.

2. метод укрупнения интервалов представляет собой переход от первоначальных значений динамического ряда к ряду с большими временными промежутками. Так, месячные укрупняют в квартальные, квартальные в годовые, годовые по пятилеткам и т.д. расчет возможен как простое суммирование величин, так и расчет средних уровней за укрупненный период.

Метод простого суммирования не используется в моментных рядах, а также если уровни ряда выражены относительной или средней величиной.

В результате более четко проявляется общая тенденция развития явления. Однако она не учитывает изменения внутри укрупненных интервалов. Для более детальной характеристики тренда используют более сложные методы (3 и 4).

3. метод скользящей средней представляет собой расчет средних уровней динамического ряда по укрупненным интервалам путем последовательного смещения начала отсчета на один временной период (т.е. исключают из укрупненного интервала первые уровни и включают последующие).

Выбор интервала сглаживания (порядковой скользящей средней) обосновывается четностью/нечетностью ряда и результатом сглаживания (должна достигаться общая тенденция).

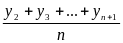; и т.д.

Например, для нечетного ряда, состоящего из 15 уровней, применяют 3-х, 5-ти, 7-ми членную скользящую среднюю (но не более половины ряда). Для трехчленной скользящей средней:

; и т.д.

Предпочтение в интервале сглаживания отдается нечетным уровням (расчетные значения в этом случае оказываются в центре сумм). При использовании четного периода используют процедуру центрирования (нахождение средней из двух смежных скользящих средних).

Метод аналитического выравнивания

4. метод аналитического выравнивания заключается в подборе адекватной математической функции, которая лучше отображает тренд.

Прямая y_t=a₀+a₁t

Парабола второго порядка y_t=a₀+a₁t+a₂t²

Гипербола и т.д.

Где а₀ – средний выравненный уровень в момент или период, принятый за начало отсчета времени;

а₁ – средний абсолютный прирост за единицу изменения времени.

Для расчета параметров тренда а₀, а₁, а₂ используют метод наименьших квадратов (МНК).

Так, например, для выравнивания по прямой y_t=a₀+a₁t система нормальных уравнений имеет вид: