1. Средняя арифметическая простая и взвешенная, средняя гармоническая: понятие и порядок расчета.

Под средней арифметической понимается такое значение признака, которое имела бы каждая единица совок-ти, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совок-ти.

Средняя арифметическая есть частное от деления суммы вариант на их число. , при ее построении необходимо просуммировать варианты и полученную сумму разделить на число вариант. Если среди вариант есть одинаковые величины, то их обьединяют в группы, умножая варианту на частоту, такое умножение наз-ся взвешиванием, а число единиц, имеющих одинаковое значение наз-ся весами. Вычисление производится по формуле:

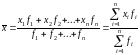
Порядок расчета: умножаем варианты на веса, складываем их, складываем веса, сумму произведения делим на сумму весов.

Средняя гармоническая величина как и средняя арифметическая может быть простой и взвешенной. Если веса у каждого признака равны, то можно использовать среднюю гармоническую простую:

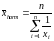
Однако в стат-ой практике чаще применяется средняя гармоническая взвешанная: .

2. Средние показатели в рядах динамики.

· Средний уровень интервального ряда динамики абсолютных величин (равные интервалы). Применяется ариф-ая простая: .

· Средний уровень интервального ряда динамики абсолютных величин (неравные интервалы). Применяется арифм-ая взвешенная: , где Т-общая продолжительность периода, t - величина интервала.

· Интервальный ряд относительных величин. Применяется средняя геометрическая:

.

· Моментный ряд с равноотстоящими моментами времени. Применяется средняя хронологическая: .

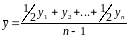·Моментный ряд с неравноотстоящими датами. Применяется средняя ариф-ая взвешанная: .

3. Мода и медиана, как структурные средние, их использование.

Это особые разновидности средних величин, которые вытекают из хар-ки стат-го ряда и не являются рез-том к.-л. алгеб-их действий.

Мода-величина признака, кот чаще всего встречается в данной совок-ти. В вариац-м ряду это будет варианта, имеющая наибольшую частоту. Применяется в том случае, когда можно охар-ть наиболее часто встречающуюся величину признака: ·для расчета показателей, хар-щих ассиметричность распр-ия; ·в торговле для опред-ия наиболее распростр-ых размеров одежды и обуви; ·в выборочном исслед-ии для отбора наиболее типичных единиц изучаемой совок-ти; ·для пересчета условно-натуральных единиц измерения. Расчет моды в интервальном ряду происходит по формуле: , где Xm0-нижняя граница модального интервала; к-коэфф-нт, показывающий величину модального инт-ла; Fm0-частота модального инт-ла; Fm0-1-частота инт-ла, предшествующего модальному инт-лу; Fm0+1- частота инт-ла, следущая за модальным.

Медиана-варианта, кот находится в середине вар-го ряда. Она делит ряд пополам и по обе стороны от нее нах-ся одинаковое кол-во единиц совок-ти. Может быть 3 момента исчисления медианы: 1) в ранжированном ряду с нечетным кол-вом членов это центральное значение; 2) в ранжированном ряду с четным кол-вом членов расчитывается как полусумма двух центральных членов; 3) в интервальном ряду по формуле: , где Xme-нижняя граница медианного инт-ла; k - величина медианного инт-ла; (åf)/2 - полусумма всех частот; Sme-1 - сумма накопленных частот, предшествующих мед-му инт-лу; Fme - частота мед-го инт-ла.

Медиана используется в территориальном планировании, в аналитических расчетах для анализа хар-ра распред-ия, в статистике качества продукции и технологических процессах.

Мода и медиана определяются лишь структурой распр-ия. Поэтому их именуют структурными позиционными средними. Их часто используют как среднюю хар-ку в тех совок-тях, где расчет средней степенной невозможен или нецелесообразен.