
- •Тест № 5 линейные пространства
- •Какие из следующих утверждений являются правильными?
- •Какие из следующих утверждений являются правильными?
- •Какие из следующих утверждений являются правильными?
- •Какие из следующих утверждений являются правильными?
- •Какие из следующих утверждений являются правильными?
Тест № 5 линейные пространства
1-й вопрос
Какие из следующих утверждений являются правильными?
а) если равенство
![]() выполняется при условии, что все
коэффициенты
выполняется при условии, что все
коэффициенты![]() ,
то система
,
то система
![]() линейно зависима;
линейно зависима;
б) если равенство выполняется при условии, что все коэффициенты , то система линейно независима;
в) если равенство выполняется только при условии, что все коэффициенты , то система линейно независима;
г) если равенство
выполняется и среди коэффициентов
![]() есть отличные от нуля, то система
линейно зависима.
есть отличные от нуля, то система
линейно зависима.
Верный ответ: в), г).
Какие из следующих утверждений являются правильными?
а) если равенство выполняется и среди коэффициентов есть отличные от нуля, то система линейно независима;
б) если система линейно зависима, то найдутся такие отличные от нуля коэффициенты, что выполняется равенство ;
в) если равенство выполняется только в том случае, когда все коэффициенты , то система линейно зависима;
г) если система линейно независима, то равенство выполняется в том случае, когда все коэффициенты равны нулю.
Верный ответ: б), г).
Какие из следующих утверждений являются правильными?
а) если система линейно зависима, то равенство выполняется только в том случае, когда все коэффициенты равны нулю;
б) если система линейно зависима, то равенство выполняется в том случае, когда все коэффициенты равны нулю;
в) если система линейно независима, то равенство выполняется в том случае, когда все коэффициенты равны нулю
г) если система линейно независима, то равенство выполняется только в том случае, когда все коэффициенты равны нулю.
Верный ответ: б), в), г).
2-й вопрос
Какие из следующих утверждений являются правильными?
а) если система
содержит
![]() ,
то она линейно зависима;
,
то она линейно зависима;
б) любая линейно зависимая система содержит ;
в) система, содержащая линейно независимую подсистему, линейно независима; г) любая подсистема линейно независимой системы линейно независима.
Верный ответ: а), г).
Какие из следующих утверждений являются правильными?
а) любая линейно зависимая система содержит линейно зависимую подсистему, не совпадающую с ней самой;
б) система, содержащая линейно зависимую подсистему, линейно зависима;
в) если система линейно зависима, то какой-либо из ее элементов можно представить в виде линейной комбинации остальных;
г) если система линейно зависима, то любой из ее элементов можно представить в виде линейной комбинации остальных.
Верный ответ: б), в).
Какие из следующих утверждений являются правильными?
а) если система линейно зависима, то какой-либо из ее элементов можно представить в виде линейной комбинации остальных;
б) если система линейно зависима, то любой из ее элементов можно представить в виде линейной комбинации остальных;
в) если какой-либо из элементов системы можно представить в виде линейной комбинации остальных, то эта система линейно зависима;
г) если любой из элементов системы можно представить в виде линейной комбинации остальных, то эта система линейно зависима;
Верный ответ: а), в), г).
3-й вопрос
Из следующих систем векторов линейно зависимыми являются:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
Верный ответ: б), в), г).
Из следующих систем векторов линейно зависимыми являются:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
Верный ответ: а), б), в).
Из следующих систем векторов линейно зависимыми являются:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
Верный ответ: в), г), д).
Из следующих систем векторов линейно независимыми являются:
а) ; б) ; в) ;
г) ; д) .
Верный ответ: а), д).
Из следующих систем векторов линейно независимыми являются:
а) ; б) ; в) ;
г) ; д) .
Верный ответ: г), д).
Из следующих систем векторов линейно независимыми являются:
а) ; б) ; в) ;
г) ; д) .
Верный ответ: а), б).
Из следующих систем функций линейно зависимыми являются:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
Верный ответ: б), в), г).
Из следующих систем функций линейно зависимыми являются:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
Верный ответ: а), в), г).
Из следующих систем функций линейно зависимыми являются:
а) ; б) ; в) ; г) ; д) .
Верный ответ: а), в), д).
Из следующих систем функций линейно независимыми являются:
а) ; б) ; в) ; г) ; д) .
Верный ответ: а), д).
Из следующих систем функций линейно независимыми являются:
а) ; б) ; в) ; г) ; д) .
Верный ответ: б), д).
Из следующих систем функций линейно независимыми являются:
а) ; б) ; в) ; г) ; д) .
Верный ответ: б), г).
4-й вопрос
Если векторы линейно независимы, то ранг матрицы, составленной из их координатных столбцов:
а) равен количеству этих векторов;
б) больше количества этих векторов;
в) меньше количества этих векторов;
г) другой ответ.
Верный ответ: а).
Если векторы линейно зависимы, то ранг матрицы, составленной из их координатных столбцов:
а) равен количеству этих векторов;
б) больше количества этих векторов;
в) меньше количества этих векторов;
г) другой ответ.
Верный ответ: в).
5-й вопрос
Если ранг матрицы, составленной из координатных столбцов векторов, равен их количеству, то эти векторы:
а) линейно зависимы;
б) линейно независимы;
в) такого не может быть.
Верный ответ: б).
Если ранг матрицы, составленной из координатных столбцов векторов, больше их количества, то эти векторы:
а) линейно зависимы;
б) линейно независимы;
в) такого не может быть.
Верный ответ: в).
Если ранг матрицы, составленной из координатных столбцов векторов, меньше их количества, то эти векторы:
а) линейно зависимы;
б) линейно независимы;
в) такого не может быть.
Верный ответ: а).
6-й вопрос
В линейном пространстве
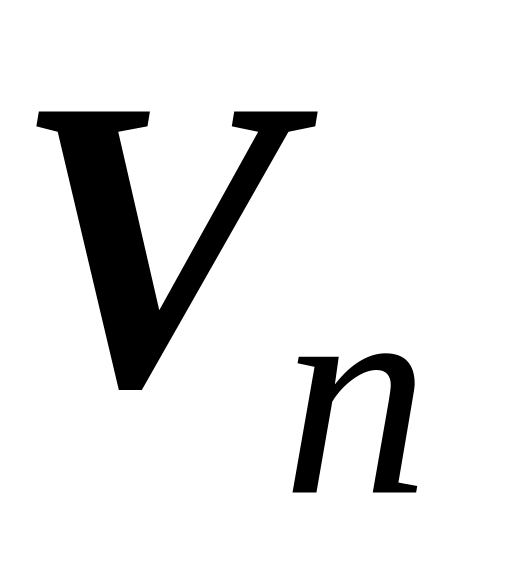 заданы два базиса:
заданы два базиса:
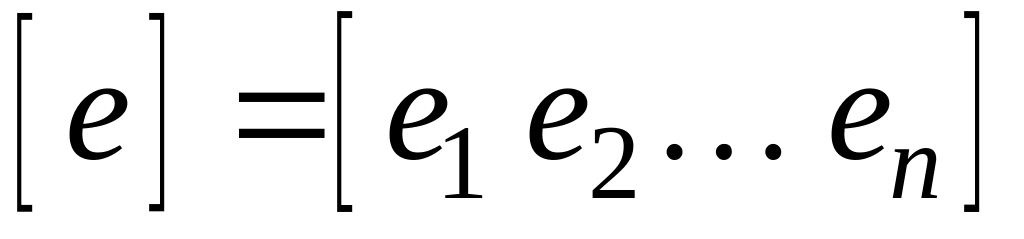 и
и
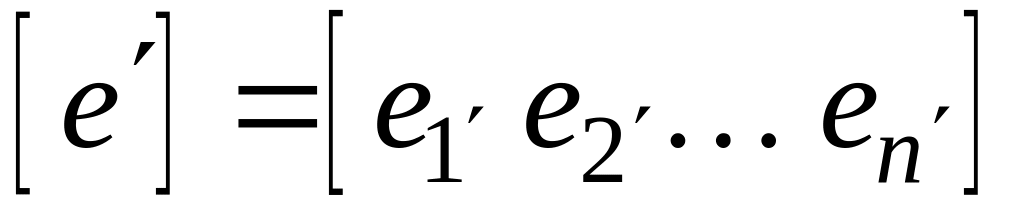 .
Если
.
Если
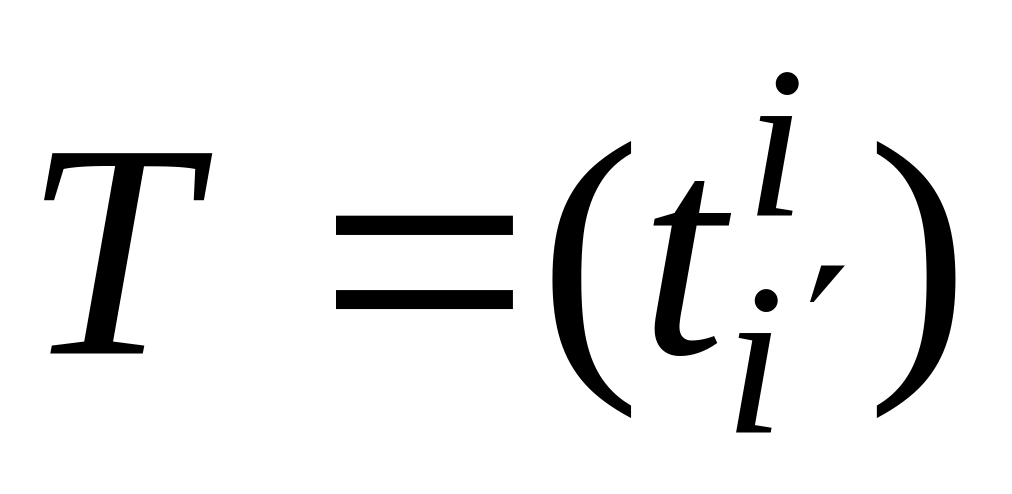 – матрица перехода от первого из них
ко второму,
– матрица перехода от первого из них
ко второму,
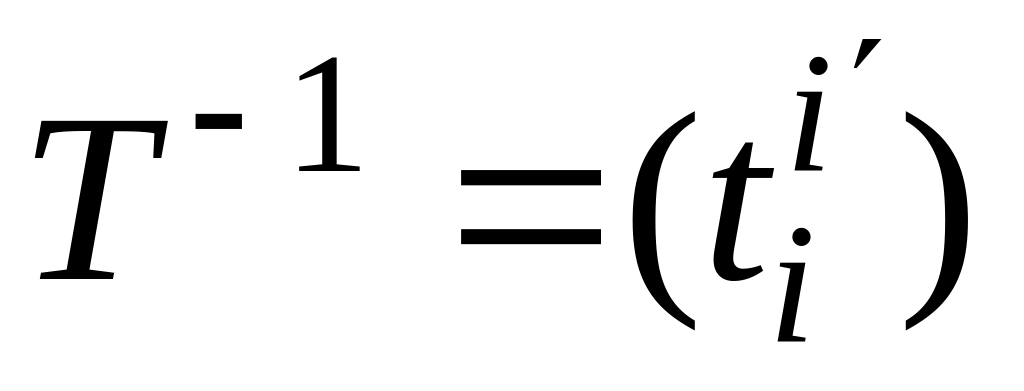 – обратная к ней, то справедливы
следующие равенства:
– обратная к ней, то справедливы
следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Верный ответ: б).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, то справедливы следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Верный ответ: а).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, то справедливы следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
.
;
в)
.
Верный ответ: в).
7-й вопрос
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, то справедливы следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ: а), б).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, то справедливы следующие равенства:
а) ; б) ; в) ; г) .
Верный ответ: в), г).
8-й вопрос
Какие из перечисленных ниже матриц могут служить матрицами перехода от одного базиса к другому в некотором линейном пространстве?
а)
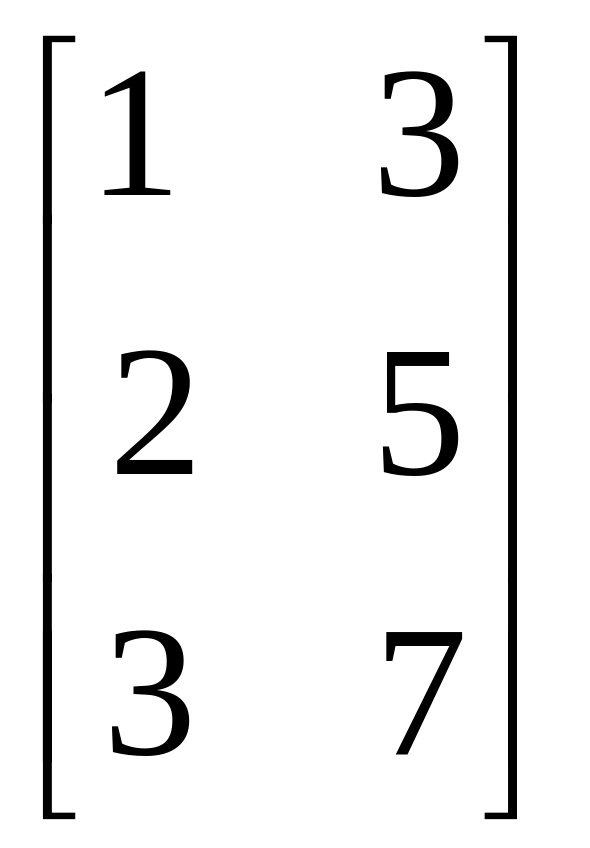 ;
б)
;
б)
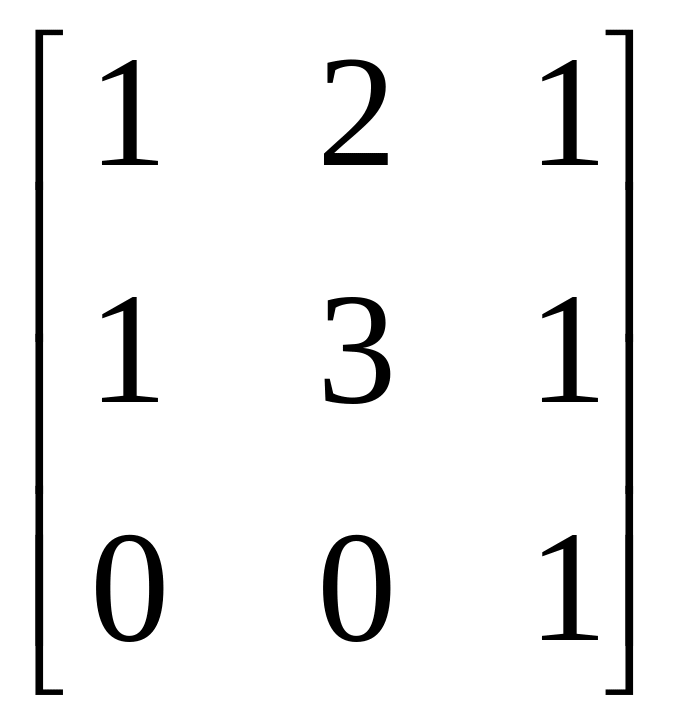 ;
в)
;
в)
 ;
г)
;
г)
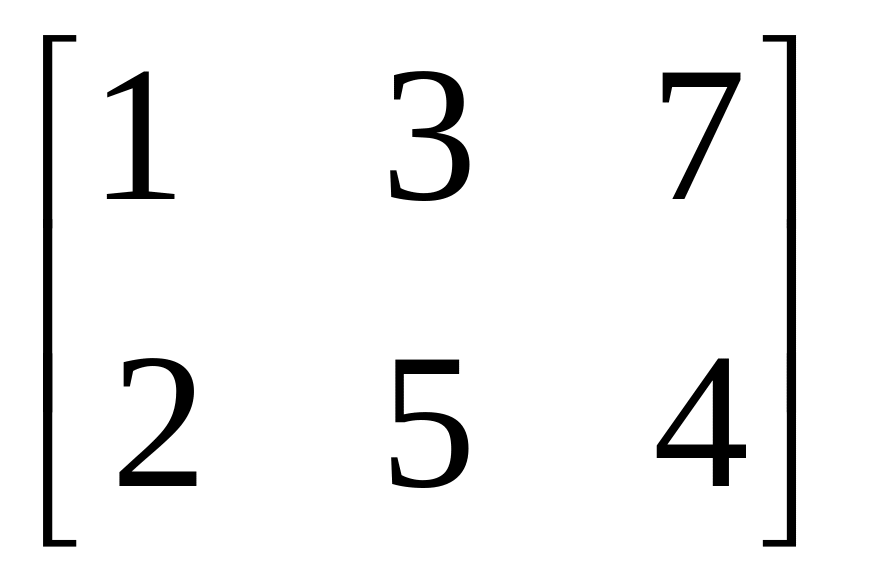 .
.
Верный ответ: б).
Какие из перечисленных ниже матриц могут служить матрицами перехода от одного базиса к другому в некотором линейном пространстве?
а)
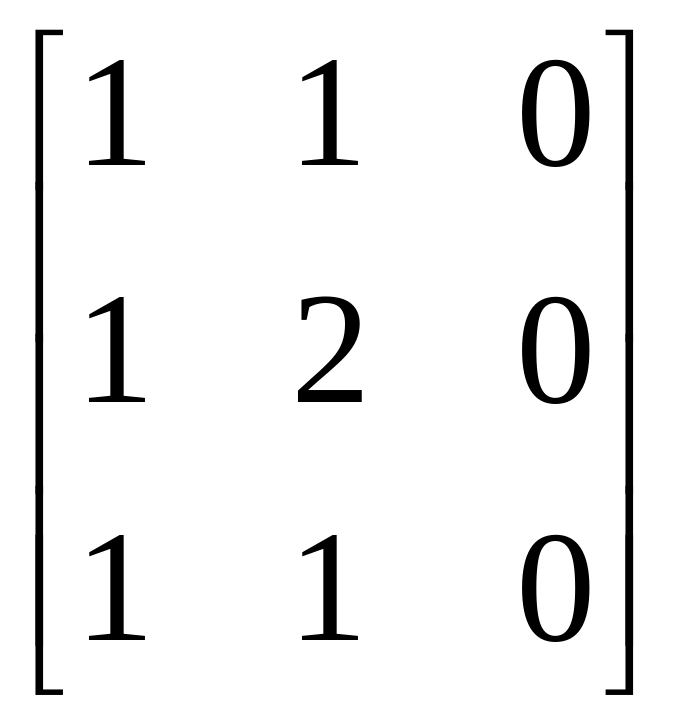 ;
б)
;
в)
;
б)
;
в)
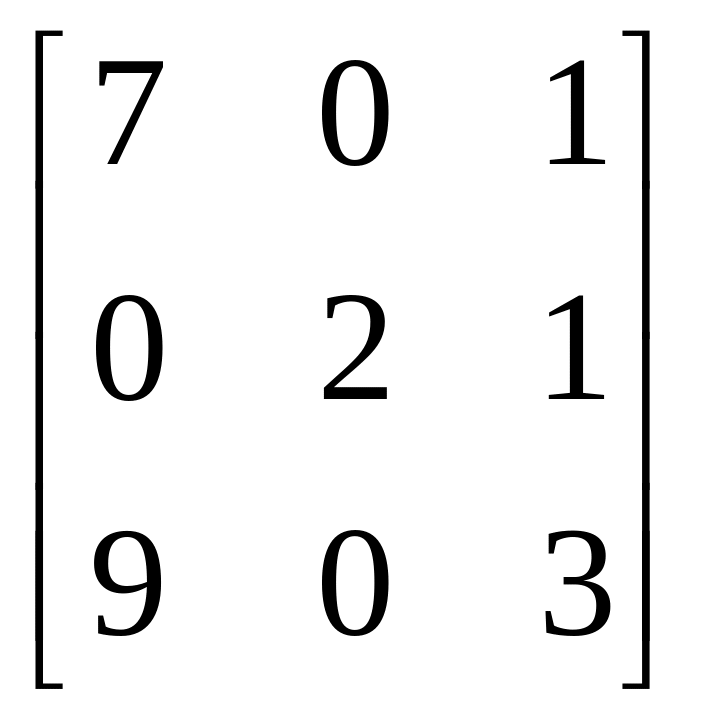 ;
г)
.
;
г)
.
Верный ответ: в).
9-й вопрос
Матрицей перехода от базиса
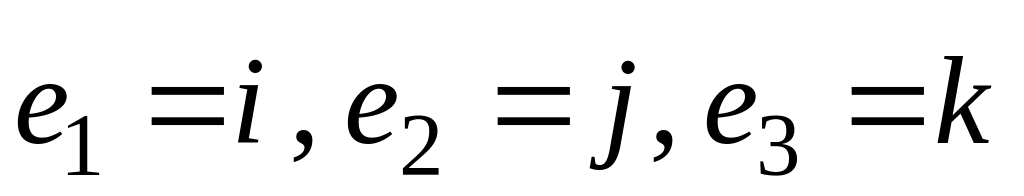 к базису
к базису
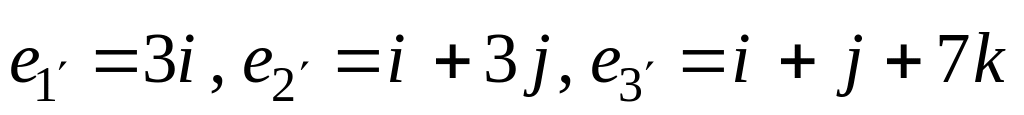 :
является следующая:
:
является следующая:
а)
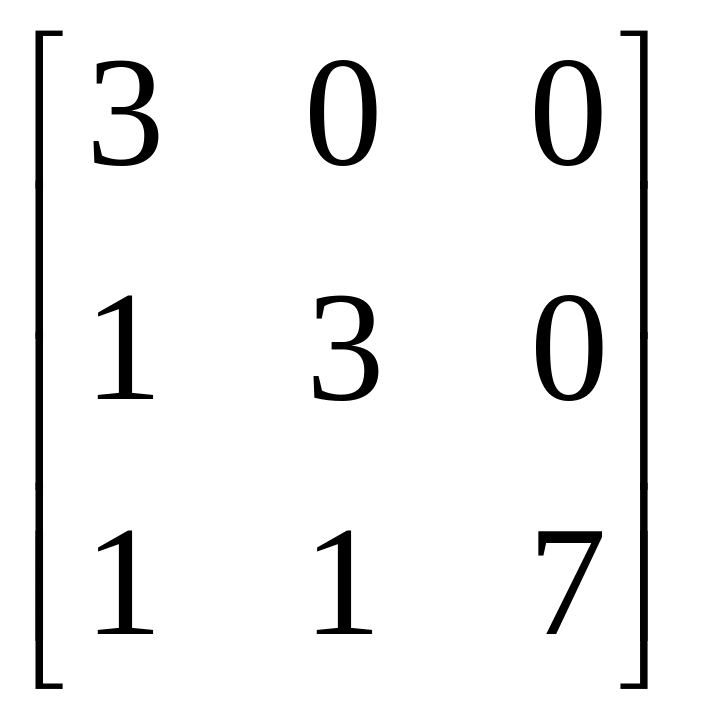 ;
б)
;
б)
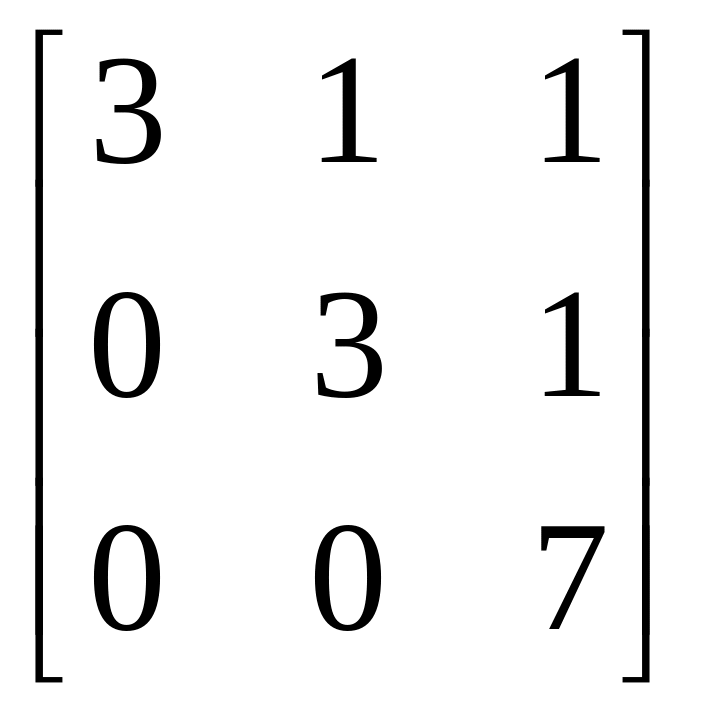 ;
в)
;
в)
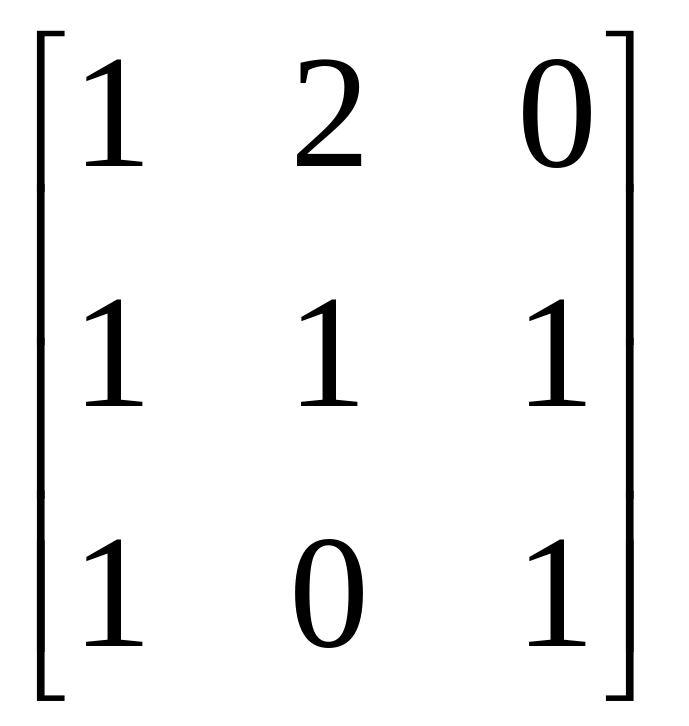 ;
г) другой ответ.
;
г) другой ответ.
Верный ответ: б).
Матрицей перехода от базиса
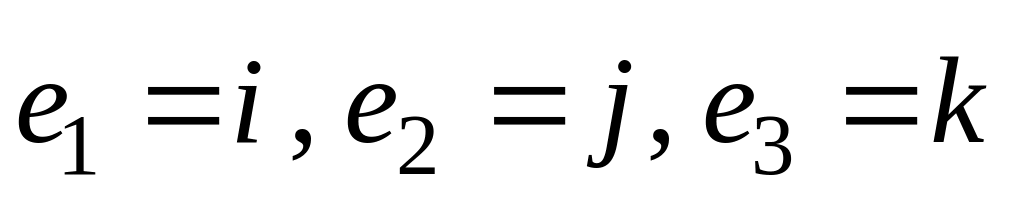 к базису
к базису
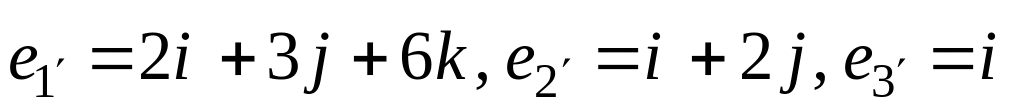 :
является следующая:
:
является следующая:
а)
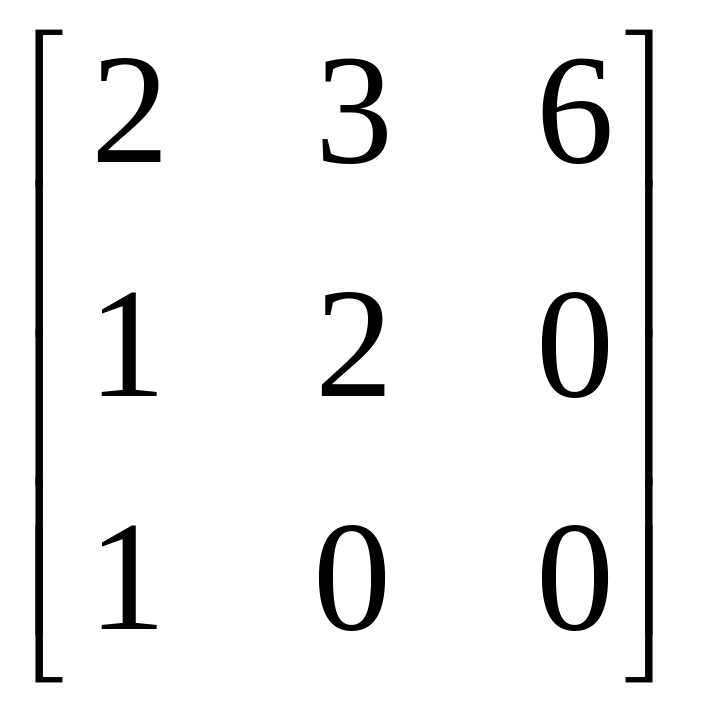 ;
б)
;
б)
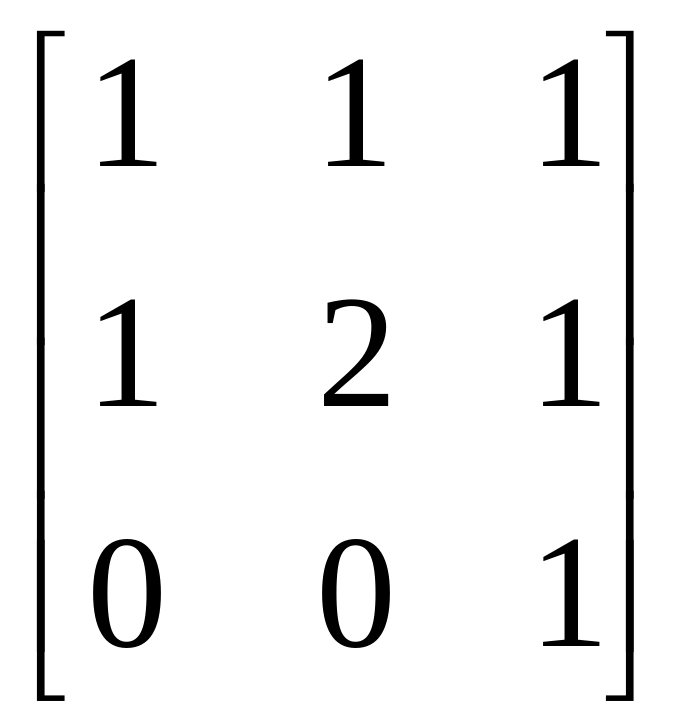 ;
в)
;
в)
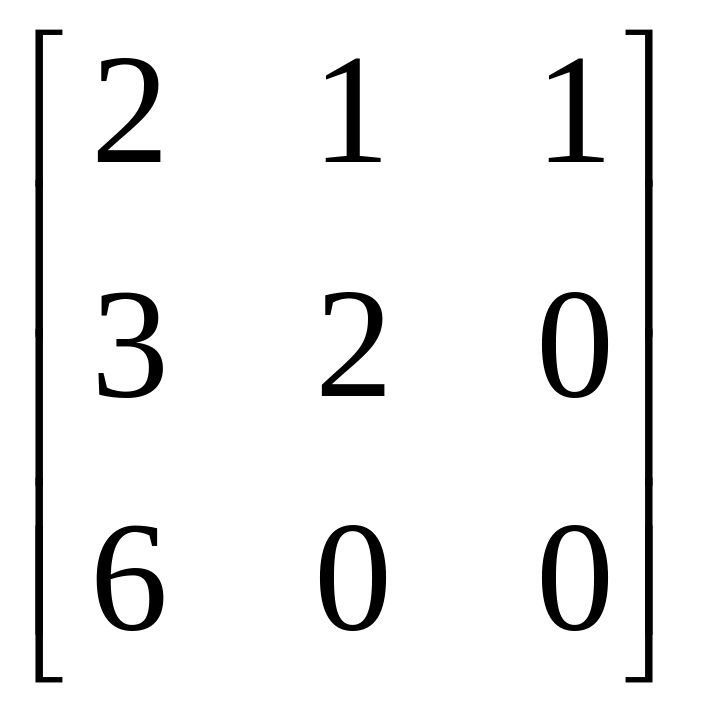 ;
г) другой ответ.
;
г) другой ответ.
Верный ответ: в).
В пространстве свободных векторов матрица
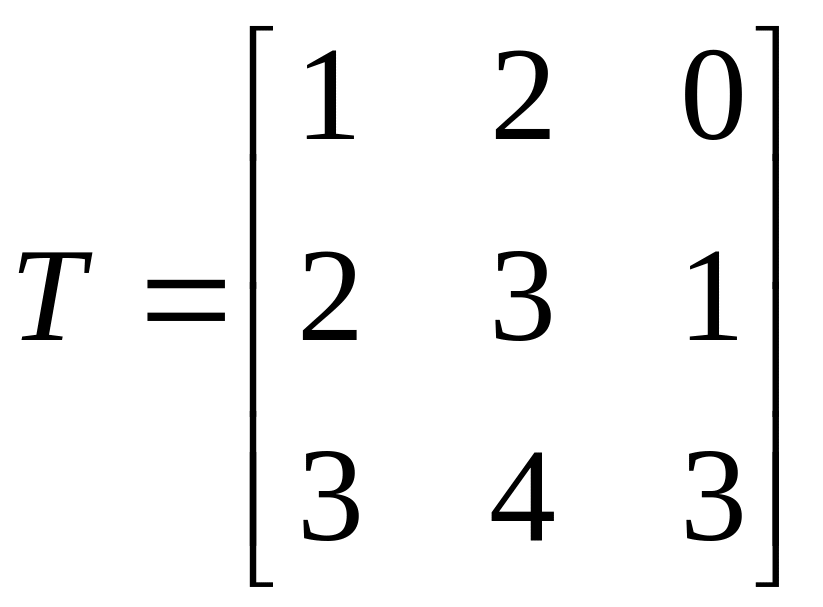 является матрицей перехода от базиса
является матрицей перехода от базиса
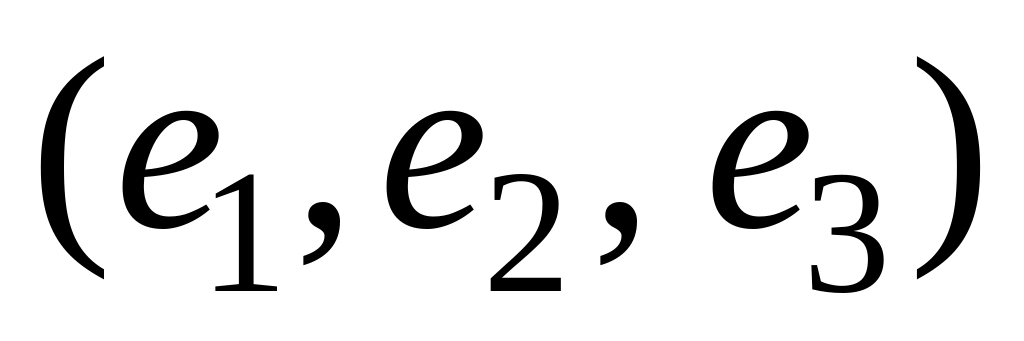 к базису
к базису
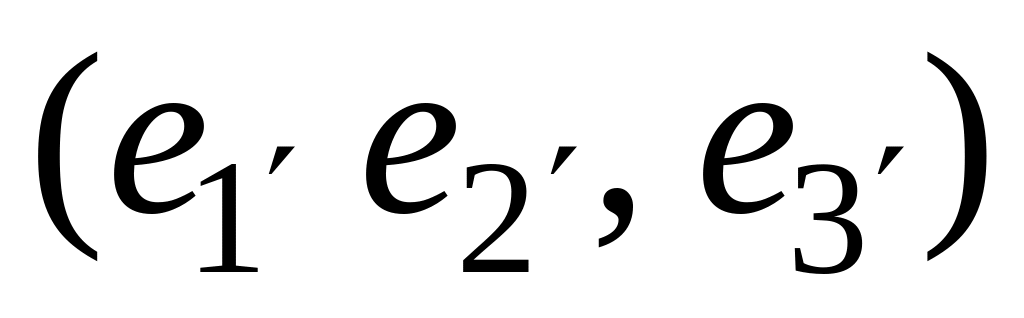 .
Какие из приведенных равенств будут
верными?
.
Какие из приведенных равенств будут
верными?
а)
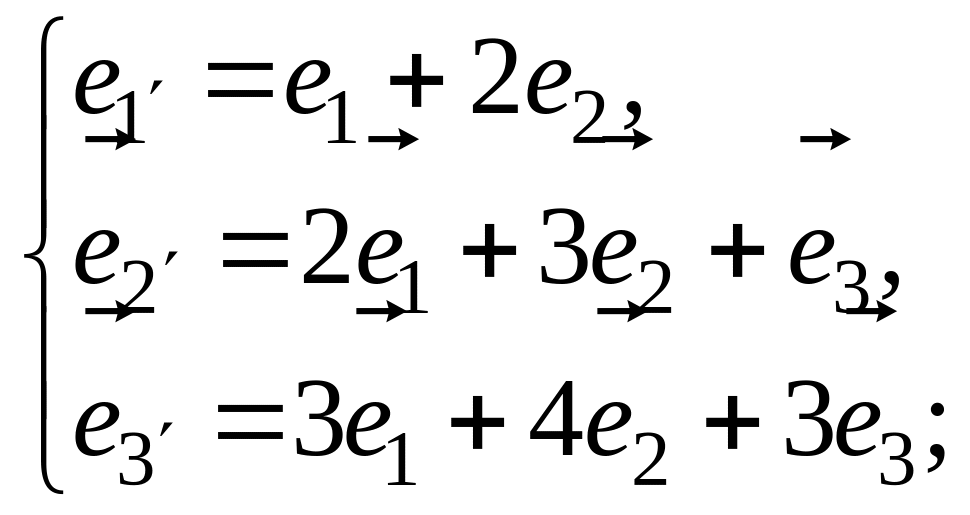 ;
б)
;
б)
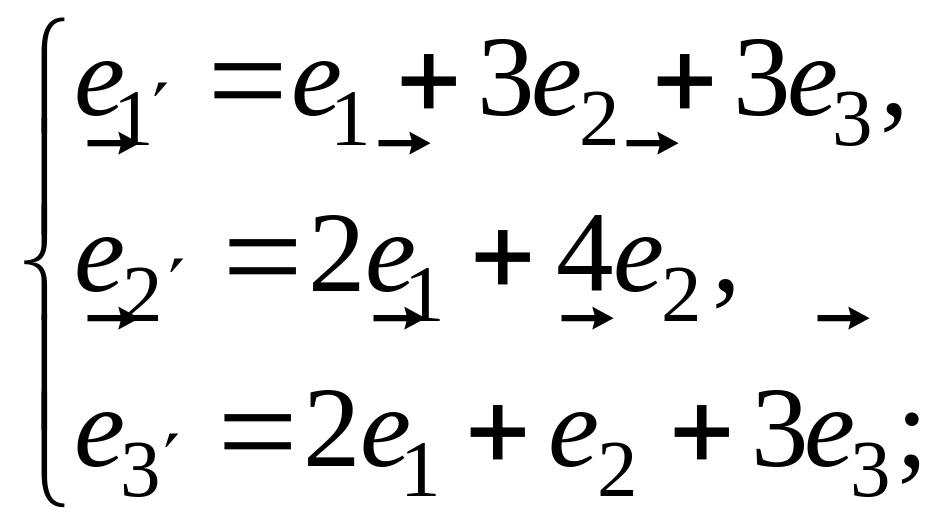 ;
в)
;
в)
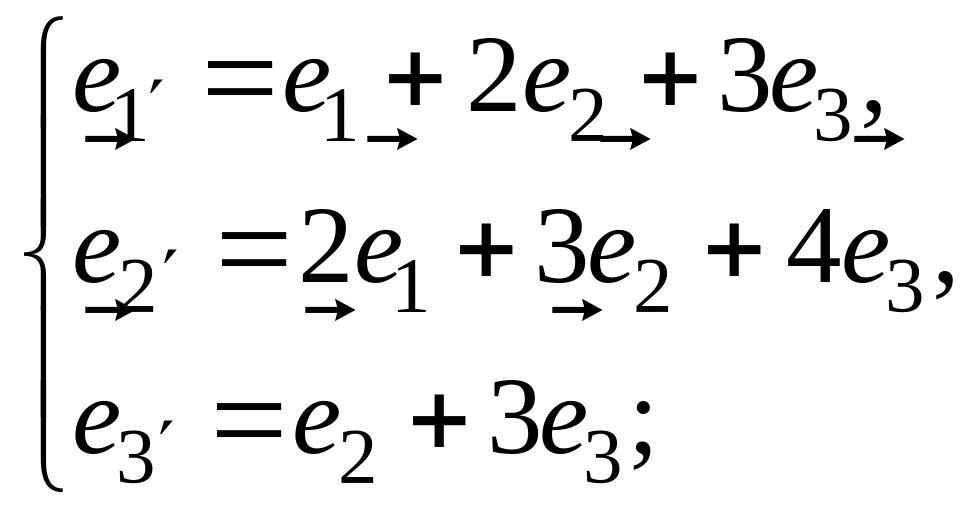 ;
г) другой ответ.
;
г) другой ответ.
Верный ответ: в).
В пространстве свободных векторов матрица
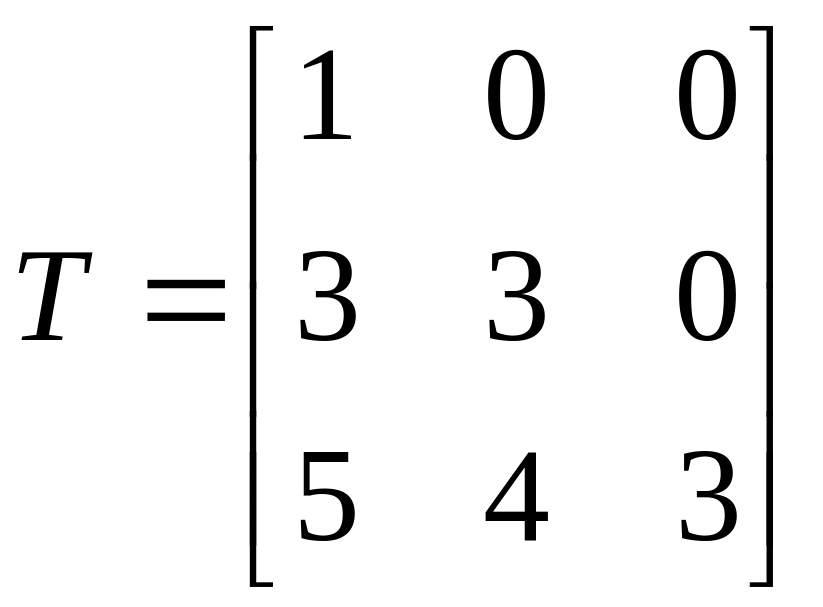 является матрицей перехода от базиса
к базису
.
Какие из приведенных равенств будут
верными?
является матрицей перехода от базиса
к базису
.
Какие из приведенных равенств будут
верными?
а)
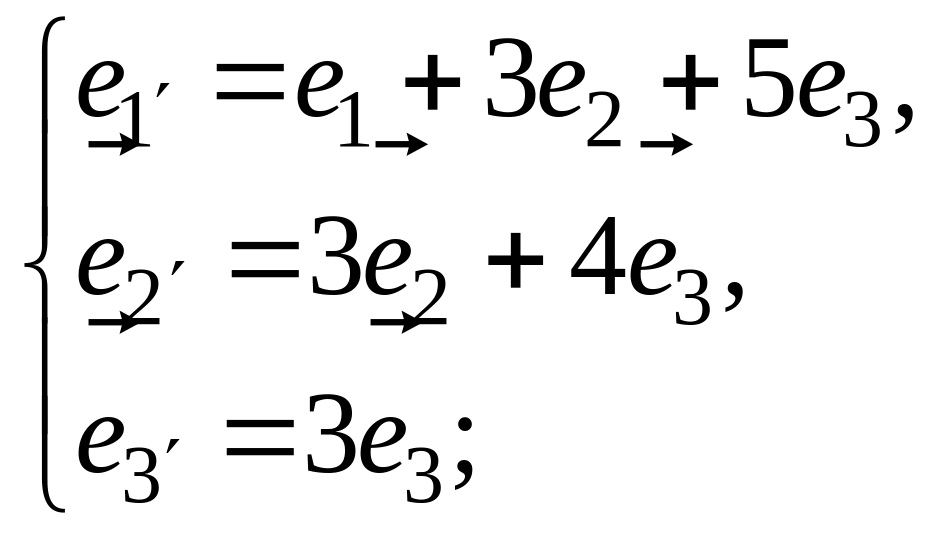 ;
б)
;
б)
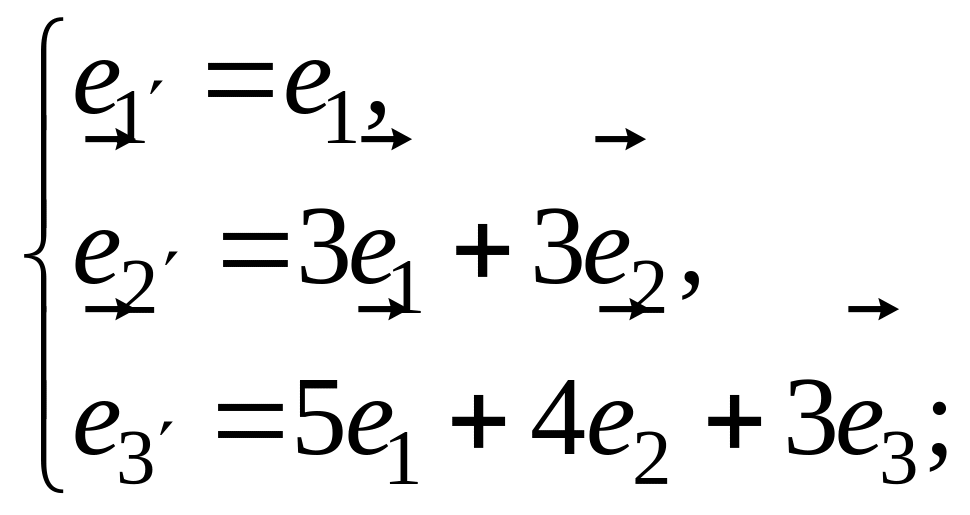 ;
в)
;
г) другой ответ.
;
в)
;
г) другой ответ.
Верный ответ: а).
10-й вопрос
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней,
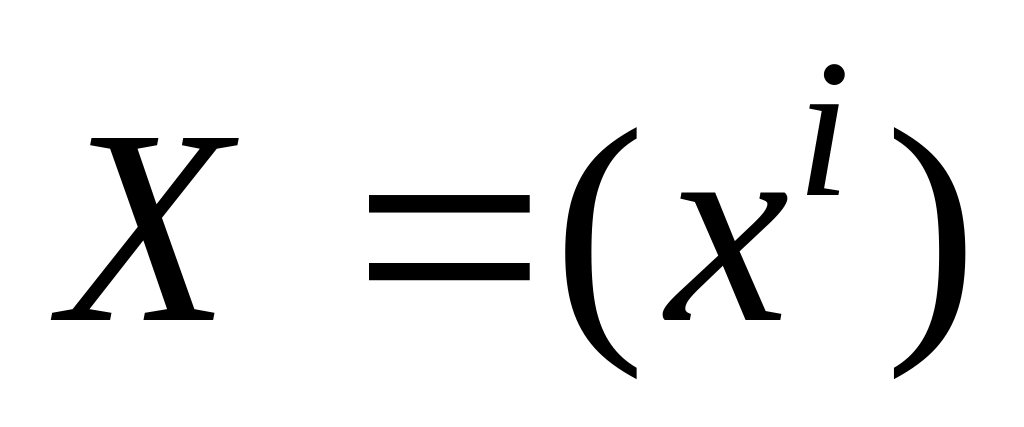 и
и
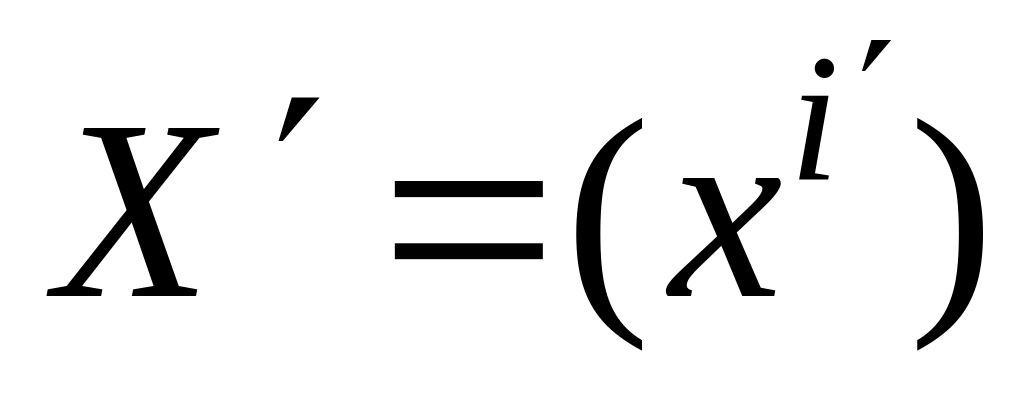 – координатные столбцы вектора
– координатные столбцы вектора
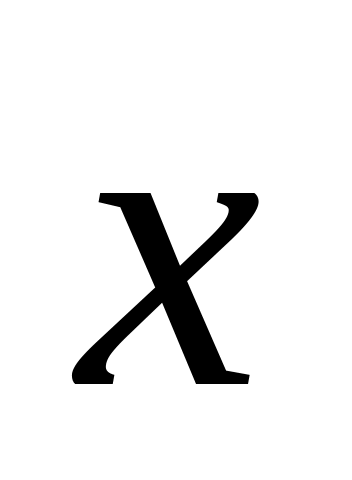 в первом и во втором базисе соответственно,
то справедливы следующие равенства:
в первом и во втором базисе соответственно,
то справедливы следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ: в), г).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, и – координатные столбцы вектора в первом и во втором базисе соответственно, то справедливы следующие равенства:
а)
;
б)
![]() ;
в)
;
г)
.
;
в)
;
г)
.
Верный ответ: а), г).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, и – координатные столбцы вектора в первом и во втором базисе соответственно, то справедливы следующие равенства:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Верный ответ: в), г).
В линейном пространстве заданы два базиса: и . Если – матрица перехода от первого из них ко второму, – обратная к ней, и – координатные столбцы вектора в первом и во втором базисе соответственно, то справедливы следующие равенства:
а) ; б) ; в) ; г) .
Верный ответ: б) , г).
