18. Побудова системи рівнянь для визначення коефіцієнтів кубічних сплайнів

Нехай задані вузлові точки Р0,Р1…Рn

Х0<X1<…<Xn

h=

t=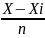

на кожному відрізку tє[0;1] Si=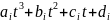

4n – невідомих коефіцієнти. Для їх знаходження побудуємо множину рівнянь використовуючи такі умови поведінки сплайна:

1. Співпадіння значення сплайна з вузловими точками S(Xi)=Yi

2. Неперервність сплайна у цих вузлових точках Si+1(0)=Si(1)

3. Неперервність першої похідної сплайна

4. Неперервність другої похідної сплайна

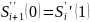
З першої нерівності отримали:

Di=yi

=>

=>

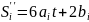Провівши перетворення отримаємо:

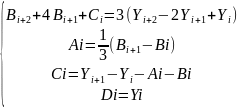
19. Переваги і недоліки растрової структури даних; векторної структури даних.

Найважливішою перевагою растрової моделі є простий зв'язок між координатами і типом інформації. Основним недоліком растрової моделі є великий обсяг пам’яті, тому використовують різні методи стискання растрових файлів.

Перевагами векторної моделі є те, що вона займає мало місця в пам’яті, дозволяє виконувати розрахунки певних точок, відстаней, довжин ліній, площ полігонів, розв’язувати задачі близькості, перетину, порівняння різних геометричних фігур. Недоліком цієї моделі є: назва, модель «спагеті» -- злиття ліній, неспівпадання границь( при записі полігонів по одній лінії проходять 2 рази).

20. Поняття про квадротомічне дерево. Приклад

Одним із методів стискання є пірамідальне кодування. Будується деревоподібна структура – кожен вищий рівень є узагальнення нижчих рівнів – квадрадерево.

Якщо 4 комірки нижчого рівня є однаковими, то вони кодуються лише один раз (0). Якщо 4 комірки різні, то їх позначають (1).

Приклад:

Квадрат омічне дерево 28 символів, кожен символ кодується 3 способами, отже к-сть інформації в квадрат омічному дереві = 84.

Початкова к-сть інформації 256*2=512. Ефективність кодування = 512/84=6,09.