Національний авіаційний університет
Лекція № 4.4
Теорія інформації та кодування Побудова завадостійких кодів. Двійкові коди
2013
Вступ
В попередній лекції при розгляді питання щодо виявлення факту наявності та можливого корегування спотворень був розглянутий, як найпростіший варіант формування надлишкових символів, виходячи із виразу:
,
(1)
розглянута потрібна і допустима надлишковість кодів та сформульована задача її мінімізації.
Отже, надалі розглянемо деякі із завадостійких кодів.
Лекція № 4.4 − “Побудова завадостійких кодів. Двійкові коди”. В лекції будуть розглянуті наступні учбові питання:
1. Способи завдання завадостійких кодів 5
1. Способи завдання завадостійких кодів 5
6
a1 6
a2 6
a3 6
b1 6
b2 6
1 6
0 6
0 6
1 6
1 6
0 6
2 6
0 6
1 6
0 6
1 6
1 6
3 6
0 6
1 6
1 6
0 6
1 6
4 6
1 6
0 6
0 6
0 6
1 6
5 6
1 6
0 6
1 6
1 6
1 6
6 6
1 6
1 6
0 6
1 6
0 6
7 6
1 6
1 6
1 6
0 6
0 6
8 6
0 6
0 6
0 6
0 6
0 6
2. Двійкові коди з перевіркою на парність або на непарність (контроль по модулю 2) 9
2. Двійкові коди з перевіркою на парність або на непарність (контроль по модулю 2) 9
3. Двійкові матричні коди 10
3. Двійкові матричні коди 10
4. Код Хеммінга 12
4. Код Хеммінга 12
Способи завдання завадостійких кодів
При завданні коду звичайно указують, які інформаційні одиничні елементи базового кодового слова і як беруть участь у формувань кожного з k перевірочних символів.
Перший спосіб завдання − описовий, коли приводиться словесно − формульний опис процедури розрахунку контрольних символів при відомих інформаційних. При завданні коду можна вказати всі дозволені для цього коду комбінації.
Наприклад, для коду з n = 5, m = 3 і k = 2 кожен перевірочний символ bі може визначатися за правилом:
b1
= a2
a3,
b2
= a1
a2,
де аі інформаційні символи. Комбінація такого коду записується у вигляді b2b1a3a2a3. При завданні коду можна вказати всі дозволені для цього коду комбінації. При більш формалізованому підході це є еквівалентним завданню системи перевірочних рівнянь, що визначають правила формування перевірочних символів по відомим інформаційним:
,
де:
позначка
означає
додавання за певним модулем, наприклад,
за
модулем 2.
j − номер перевірочного символу;
і − номер інформаційного символу;
сіj − коефіцієнти, що приймають значення відповідно до правил формування конкретних кодів, наприклад, сіj = 1.
Другий спосіб завдання − шляхом перерахуванням кодових слів, тобто складанням таблиці − списку всіх кодових слів коду.
Приклад. У таблиці 2 представлені всі кодові слова (5, 3) − двійкового коду (aі − інформаційні, а bі − перевірочні символи).
Таблиця 2 Таблиця кодових слів коду (5,3) |
|||||
|
a1 |
a2 |
a3 |
b1 |
b2 |
1 |
0 |
0 |
1 |
1 |
0 |
2 |
0 |
1 |
0 |
1 |
1 |
3 |
0 |
1 |
1 |
0 |
1 |
4 |
1 |
0 |
0 |
0 |
1 |
5 |
1 |
0 |
1 |
1 |
1 |
6 |
1 |
1 |
0 |
1 |
0 |
7 |
1 |
1 |
1 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
Третій спосіб завдання − у вигляді матриці, що породжує, в так званій канонічній формі. При цьому перші (праві) m стовпців цієї матриці містять по одній одиниці і утворюють одиничну матрицю. Решта стовпців указує правила формування перевірочних одиничних елементів.
Так, для приведеного прикладу двійкового коду матриця, що породжує, в канонічній формі має вигляд:
G
(5, 3) =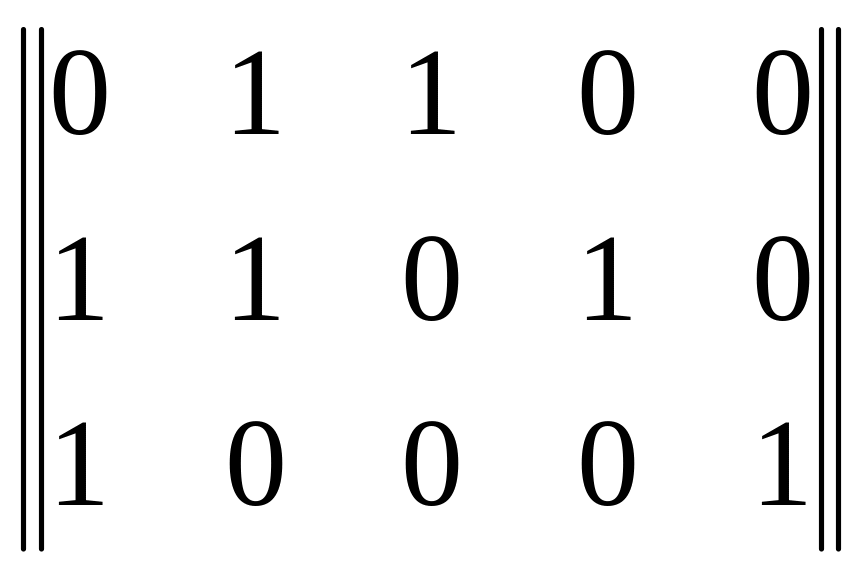
З прикладу видно, що перші три стовпці складають одиничну матрицю
І
(m,
m)
=
,
четвертий
стовпець показує, що при формуванні
першого перевірочного символу беруть
участь другий і третій інформаційні
символи. П’ятий стовпець що при нормуванні
другого перевірочного символу беруть
участь перший і другий інформаційні
символи. Таким чином, при написанні
матриці, що породжує, в канонічній формі
спочатку пишуть одиничну матрицю
розміром m
m,
а потім приписують до неї k
стовпців, кожний з яких показує правила
формування перевірочних символів. Тобто
матрицю, що породжує, в канонічній формі
можна позначити таким чином:
G
(n,
m)
=
.
Варіантів запису матриць, що породжує, в загальному випадку досить багато.
Канонічна форма матриці, що породжує, може бути також записаною у вигляді
G
(n,
m)
=
.
При такому способі опису процес кодування математично записується у вигляді добутку матриці-рядка, що відображає вихідну кодову комбінацію, на матрицю, що породжує. (При виконанні всіх математичних перетворень додавання здійснюється по модулю 2). Припустимо, що вихідна кодова комбінація записана так:
А
=
.
Тоді процес кодування запишеться у вигляді
F = А G (n, m) = bkbk-1…b1amam-1…a1,
де, як і раніше, bі (і = 1, 2,...k) – перевірочні, а aі (і = 1, 2,..., m) – інформаційні символи.
В результаті кодування одержимо комбінацію, де перші m символів − інформаційні (aі), а останні k символів − перевірочні (bі). Наприклад, закодуємо кодову комбінацію A = 1011 кодом (7, 4) з матрицею, що породжує,
G
(7, 4) =
.
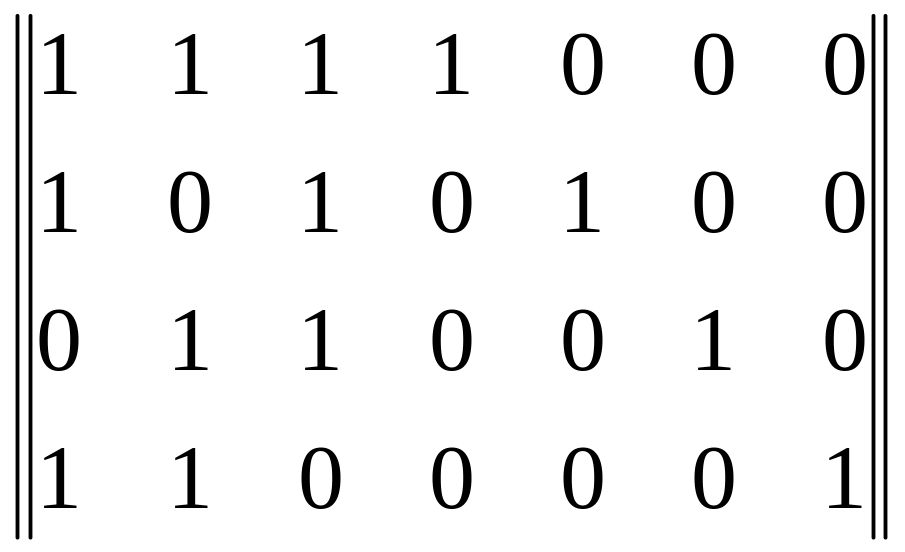Для цього перемножимо матриці A і G: F = A G (7, 4). Одержимо
F
=
= 0101011,
де перші чотири символи (1011) − інформаційні, а останні три (010) − перевірочні.
При декодуванні на приймальній стороні здійснюється стільки ж перевірок, скільки виконувалося і на передаючій, Кожна перевірка включає, окрім інформаційних символів, перевірочні символи.
Результат цих перевірок указує або тільки на наявність або відсутність спотворення, або ще й номер спотвореного символу.