18

Національний авіаційний університет

Теорія інформації та кодування

Лекція № 4.6

Циклічні коди в режимі виправлення спотворень. Перемежування та виграш від кодування

2013

Вступ

Лекція № 4.6 − “Циклічні коди в режимі виправлення спотворень. Перемежування та виграш від кодування”. В лекції будуть розглянуті наступні учбові питання:

1 Способи опису циклічних кодів 3

2 Виявлення і виправлення спотворень в циклічних кодах 5

3 Метод перемежування 10

4 Визначення необхідної глибини перемежування 12

5 Виграш від кодування 14

6 Визначення шляхів зменшення надлишковості кодів 16

1Способи опису циклічних кодів

Циклічні коди, як і інші завадостійкі коди можуть бути заданими, по-перше, описово, коли приводиться словесно − формульний опис процедури розрахунку контрольних символів при відомих інформаційних. Таке завдання цих кодів щойно розглянуто.

По-друге, шляхом перерахуванням кодових слів, тобто складанням таблиці − списку всіх кодових слів коду. Цей можливий спосіб розглядати не будемо.

Третій спосіб завдання циклічних кодів − у вигляді матриць використовується дуже часто. Циклічний код може бути заданий породжуючою і перевірочною матрицями. Для їх побудови досить знати породжуючий Р(x) і перевірочний Н(x) багаточлени.

Тоді коди задаються перевірочними матрицями або матрицями, що породжують. Вид цих матриць визначається способом утворення циклічних кодів (роздільних несистематичних чи нероздільних систематичних) і утворюючим багаточленом Р(х). Нагадаємо, що канонічна форма матриці, що породжує, може бути записаною у вигляді

G_{(n, m)} = .

де:

I_т – одинична підматриця розмірністю т т;

– прямокутна підматриця розмірністю k т для обчислення k перевірочних символів.

Приклад. Породжуюча матриця в систематичному вигляді для (5, 3) – коду (п = 5, т = 3, k = 5 – 3 = 2) має вигляд:

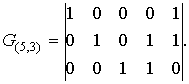
Нагадаємо, що при кодуванні вихідна кодова комбінація записується як матриця – рядок:

А_(m,1) = ,

а процес кодування здійснюється у вигляді матричного множення утворюючої матриці на цю транспоновану матрицю, в наслідок чого одержують закодоване повідомлення як матрицю – рядок:

F_(п,1) = G (n, m) = a_ma_m-1…a₁ b_kb_k-1…b₁,

де, як і раніше, b_і (і = 1, 2,...k) – перевірочні, а a_і (і = 1, 2,..., m) – інформаційні символи.

Між породжуючою і перевірочною матрицями існує однозначна відповідність, а саме:

,

а, отже, перевірочна матриця одержується із породжуючої і має вид:

,

де: I_k – одинична матриця розмірністю k k, – прямокутна транспонована матриця із породжуючої матриці G (n, m).

Приклад. Перевірочна матриця Н_{(5, 3)} із наведеної вище породжуючої матриці G_{(n, m)} має вигляд:

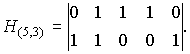
Тоді процедура декодування здійснюється у вигляді операції матричного множення транспонованої перевірочної матриці на матрицю – рядок закодованої послідовності, в наслідок чого одержують синдром спотворення як матрицю – рядок:

.

Надалі здійснюють аналіз наступних можливих ситуацій.

1. Добуток будь-якого неспотвореного кодового слова, наприклад F_(1,n), на транспоновану перевірочну матрицю дає нульовий вектор – синдром розмірності (п – m) .

Наприклад. для коду (5, 3):

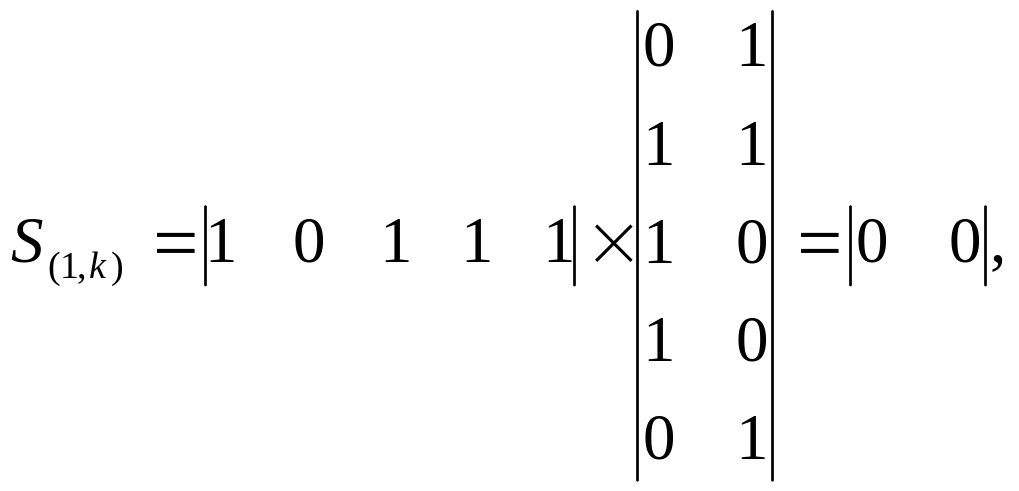
що свідчить про відсутність спотворення.

2. Добуток деякого спотвореного кодового слова, тобто з слова із помилкою, на транспоновану перевірочну матрицю є ненульовим синдромом:

що свідчить про наявність спотворення.