Основні дані броньових пластинчастих магнітопроводів

Тип магніто- провода				Розміри , мм																										Пере-тин магні-топро-вода, см2					Дов-жина магніт-ної силової лінії, см				Основ-ний параметр транс-форма-тора, см4				Орієнтована потужність
																																											f, Гц
				a				h				c				C				H					b					Sст					lст				SстS0				5					400
1	2				3				4				5				6				7					8					9					10					11					12
Ш 09Х09			9				22,5				9				36				31,5					9					0,81					7,72				1,62				2					15
Ш 09Х12																								12					1,08									2,16				2,5					17
Ш 12Х10	12				30				12				48				42					10					1,08					10,03						4,3				5		30
Ш 12Х12																							12					1,44									5,2			5,5					33
Ш 12Х16																							16					1,92									6,8			7					44
Ш 12Х20																							20					2,4									8,6			8,5					52
Ш 12Х25																							25					3									10,8			10					60
Ш 16Х12	16				40				16				64				56				12					1,92					13,7					12,1					12					72
Ш 16Х16																							16					2,56									16,6			15					92
Ш 16Х20																							20					3,2									20,5			18					110
Ш 16Х25																							25					4									25,6			22					130
Ш 16Х32																							32					5,12									32,6			27					150
Ш 20Х20	20				50				20				80				70				20					4					17,4					40					32					185
Ш 20Х25																							25					5									50			40					220
Ш 20Х32																							32					6,4									64			48					260
Ш 20Х40																							40					8									80			58					320
Ш 25Х16	25				62,5				25				100				87,5				16					4,8					21,4					62,5					50					280
Ш 25Х20																							20					5									78			60					325
Ш 25Х25																							25					6,25									97,5			72					385
Ш 25Х32																							32					8									125			90					480
Ш 25Х40																							40					10									156			100					525
Ш 25Х50																							50					12,5									195			130					655
Ш 32Х20	32				80				32				128				112				20					6,4					27,4					164					110					600
Ш 32Х25																							25					8									205			140					740
Ш 32Х32																							32					10,2									260			170					900
Ш 32Х40																							40					12,8									328			210					1000
Ш 32Х50																							50					16									410			250					1160
Ш 32Х64																							64					20,4									522			300					1400
Ш 40Х25		40				100				40				160				140					25					10					34,3				400			250					1250
Ш 40Х32																							32					12,6									512			310					1550
Ш 40Х40																							40					16									640			375					1750
Ш 40Х50																							50					20									800			450					2050
Ш 40Х64																							64					25,6									1025			550					2400
Ш 40Х80																							80					32									1280			600					2650

Таблиця 13

Основні дані броньових стрічкових магнітопроводов типу ШЛ

Тип магніто- провода	Розміри , мм																									Пере-тин магні-топро-вода, см2					Дов-жина магніт-ної силової лінії, см					Основ-ний параметр транс-форма-тора, см4						Орієнтована потужність
																																										f, Гц
			a				h				c				C				H				b					Sст					lст					SстS0					50				400
1					2				3				4				5				6				7					8					9					10					11				12
ШЛ 6Х6,5				6				15				6				25				22				6,5					0,39					4,7					0,35					-				4,5
ШЛ 6Х8																								8					0,48										0,43					-				5
ШЛ 6Х10																								10					0,6										0,54					-				6
ШЛ 6Х12,5																								12,5					0,75										0,67					-				7
ШЛ 8Х8				8				20				8				33				29				8					0,64					6,8					1,02					-				15
ШЛ 8Х10																								10					0,8										1,28					-				20
ШЛ 8Х12,5																								12,5					1										1,6					-				24
ШЛ 8Х16																								16					1,28										2,05					-				30
ШЛ 10Х10				10				25				10				40				35				10					1					8,5					2,5					-				37
ШЛ 10Х12,5																								12,5					1,25										3,12					-				47
ШЛ 10Х16																								16					1,6										4					-				56
ШЛ 10Х20																								20					2										5					-				67
ШЛ 12Х12,5				12				30				12				48				42				12,5					1,5					10,2					5,4					3				80
ШЛ 12Х16																								16					1,92										6,9					5				94
ШЛ 12Х20				12				30				12				48				42				20					2,4										8,7					7				112
ШЛ 12Х25																								25					3										10,8					10				135
ШЛ 16Х16		16				40				16				64				56				16					2,56					13,6					16,6				15					158
ШЛ 16Х20																						20					3,2										20,5				22					195
ШЛ 16Х25																						25					4										25,6				32					250
ШЛ 16Х32																						32					5,1										32,6				40					300
ШЛ 20Х20		20				50				20				80				70				20					4					17,1					40				45					330
ШЛ 20Х25																						25					5										50				54					380
ШЛ 20Х32																						32					6,4										64				68					450
ШЛ 20Х40																						40					8										80				86					510
ШЛ 25Х25		25				62,5				100				87,5				87,5				25					6,25					21,3					98				110					610
ШЛ 25Х32																						32					8										125				135					730
ШЛ 25Х40																						40					10										156				170					810
ШЛ 25Х50																						50					12,5										195				210					990
ШЛ 32Х32		32				80				32				128				112				32					10,2					27,3					261				260					1200
ШЛ 32Х40																						40					12,8										328				310					1400
ШЛ 32Х50																						50					16										410				390					1650
ШЛ 32Х64																						64					20,5										523				490					1940
ШЛ 40Х40		40				100				40				160				140				40					16					34,2					640				600					2200
ШЛ 40Х50																						50					20										800				690					2500
ШЛ 40Х64																						64					25,6										1025				850					3000
ШЛ 40Х80																						80					32										1280				1000					3500

Таблиця14

Орієнтовані значення спадання напруги на обмотках

Час-тота, Гц	Падіння напруги	Сумарна потужність вторинних обмоток Sн, В.А
		5…13	15…50	50…100	150…300	300…1000	1000…2500
50	%	20…13	13…6	6…4,5	4,5…3	3…1
	%	25…18	18…10	10…8	8…6	6…2
400	%	10…8	8…4	4…1,5	1,5…1	1…0,5	0,5
	%	8,5…10	10…5	5…2	2…1,2	1,2…0,5	0,5

Враховуючи, що ЕРС на один виток для кожної обмотки Е_вт=Е_i /w_i, одержуємо вираження для визначення числа витків первинної обмотки:

,

а також для кожної з вторинних обмоток.

ЕРС одного витка:

E_вт =4.44 ^.f ^.B ^.S_ст ^.K_с .

У випадку регулювання вторинної напруги зміною числа витків первинної обмотки укладання виробляється по повному числу витків W₁+W_рег, де W_рег визначається в залежності від ступеня регулювання за завданням (наприклад, при регулюванні 6% повне число витків первинної обмотки дорівнює W₁+0,06W₁).

Для того щоб розмістити обмотки в робочому просторі, потрібно накреслити вікно трансформатора і розташувати в ньому ізолюючий каркас, що виготовляється з ізоляційного картону товщиною 0,5...1,0 мм. По робочій висоті каркаса визначають число витків, розташовуваних в одному шарі, і повне число шарів, а також товщину кожної обмотки. Ескіз вікна з обмотками накреслюють у масштабі.

Число витків у шарі I-ї обмотки:

,

де: h_сл – висота шару; К_у – коефіцієнт укладання, К_у = 0,85...0,95.

Висота шару первинної обмотки h_сл1 дорівнює різниці між висотою вікна і подвоєною товщиною каркаса. Для кожної наступної обмотки висота шару зменшується на 0,5...1 мм.

Число шарів I -ї обмотки заокруглюється до більшого цілого числа.

Товщина котушки I -ї обмотки:

де: - товщина мїжшарової ізоляції, прийнята за табл.15.

Таблиця 15

Товщина міжшарової ізоляції

Діаметр провода, мм	Тип ізоляції и товщина, мм
0,1; 0,2; 0,3	Конденсаторний папір 0,001; 0,002; 0,003
0,3…0,6	Намотувальний папір 0,05
0,6…0,9	Намотувальний папір 0,07
Понад 0,9 мм	Кабельний папір 0,12

Товщина всіх котушок з обліком міжкотушкової ізоляції і товщини гільзи:

,

де: К_р= 1,05. ..1,1; = 0.7.. .2 мм (великі значення відносяться до більш великих магнітопроводів) .

Зазор між котушкою і зовнішнім стрижнем при номінальному значенні вікна складає 0,5...2 мм. При великих значеннях варто вибрати сердечник з меншим вікном.

Задача 3. Асинхронний двигун з фазним ротором.

До пункту 2.

Г-подібна заступна схема і її параметри наведені в [ 1, с. 258-282, 3, с. 146-149].

Опори обмоток статора і ротора задані у табл. 4, а для визначення опорів вітки намагнічування R_m i X_m треба скористуватися заданими параметрами холостого ходу з урахуванням енергетичної діаграми активної поттужності для цього режима. Після визначення X_m розраховується спрощене значення коефіцієнта С₁.

До пункту 3.

Для визначення усіх величин у номінальному режимі слід за заданою частотою обертання ротора n_н визначити синхронну частоту обертання поля статора n₁ і номінальне ковзання s_н. Увесь подальший розрахунок вести з використанням Г-подібної заступної схеми, з урахуванням енергетичної діаграми двигуна для режиму навантаження і рівнянь для електромагнітного момента двигуна.

При з'єднанні обмотки статора зіркою номінальна фазна напруга:

а фазний струм дорівнює лінійному:

При з'єднанні обмотки статора трикутником номінальна фазна напруга:

а фазний струм:

3.3. Номінальний електромагнітний обертальний момент двигуна, Н ^. м

,

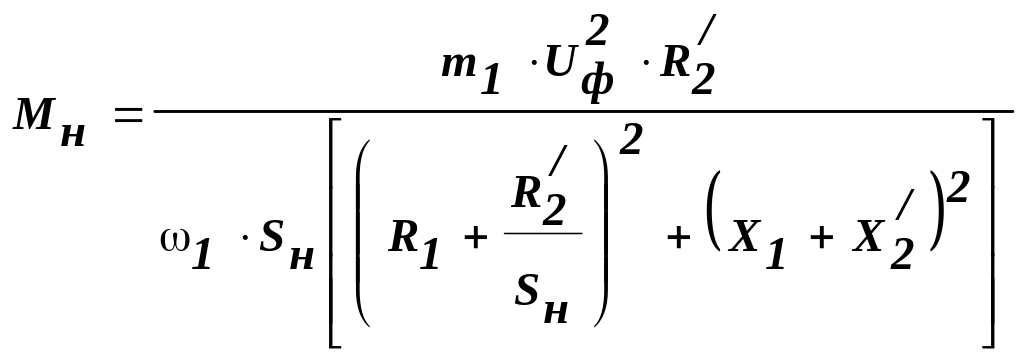де: синхронна кутова швидкість обертання магнітного поля;

m₁ - число фаз.

Номінальний обертальний момент на валу машини:

М_2н=9550Р_н/n_н,

де: Р_н – номінальна потужність, кВт.

Момент холостого ходу визначається як різниця між електромагнітним моментом і моментом на валу:

М₀ = М - М_2н.

Максимальний електромагнітний обертальний момент двигуна, Н ^. м:

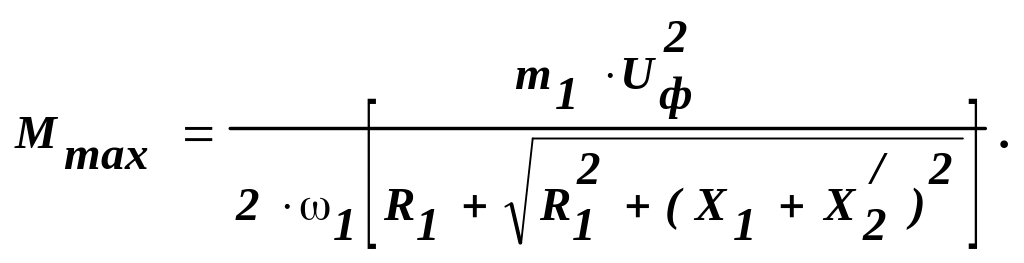
Кратність максимального моменту:

.

3.4. Струм статора при пуску двигуна (s=1) із замкненим накоротко ротором без обліку струму, що намагнічує, у цьому режимі визначається за спрощеною заступною схемою:

.

Дійсний струм ротора при пуску двигуна з короткозамкненим ротором:

,

де: K_i - коефіцієнт трансформації по струму системи статор-ротор;

Для АМ з фазним ротором К_i=К_е; К_е— коефіцієнт трансформації по ЕРС системи статор-ротор:

де: Е₁ – ЕРС обмотки статора:

Е₁=К_н ^. Uф.

Для АД з фазним ротором коефіцієнт К_н=0,95...0,98.

Треба нагадати, що обмотки ротора з’єднуються за схемою “зірка”, тому:

Коефіцієнт потужності двигуна при пуску з короткозамкненим ротором:

.

Обертальний момент при пуску двигуна з замкненим накоротко ротором (на природній характеристиці):

.

Необхідно зробити висновок про можливість запуску двигуна з короткозамкненим ротором при номінальному навантаженні.

3.5. Приведений опір фази пускового реостата, необхідний для одержання при пуску максимального значення моменту, визначається з умови s_n=s_k=1, тобто:

,

відкіля:

.

Дійсне значення опору фази пускового реостата

.

3.6. Струм статора при пуску двигуна з реостатом (на штучній характеристиці):

Дійсний струм ротора при пуску двигуна з реостатом, що забезпечує максимальне значення пускового моменту:

I_2nш = I_1nшK_i.

Коефіцієнт потужності при реостатної пуску двигуна:

Необхідно проаналізувати причини збільшення коефіцієнта потужності при пуску з реостатом у порівнянні з пуском без реостата.

3.7. Кратність пускового моменту при пуску двигуна: з короткозамкнутим ротором:

.

Кратність пускового моменту при реостатному пуску двигуна:

.

Відповідні значення кратності пускового струму:

Порівнявши отримані результати обчислень, можна зробити висновок, що введення опору пускового реостата в коло ротора АД збільшує пусковий момент при зменшенні пускового струму.

До пункту 4. Природну механічну характеристику АД розраховують по рівнянню:

.

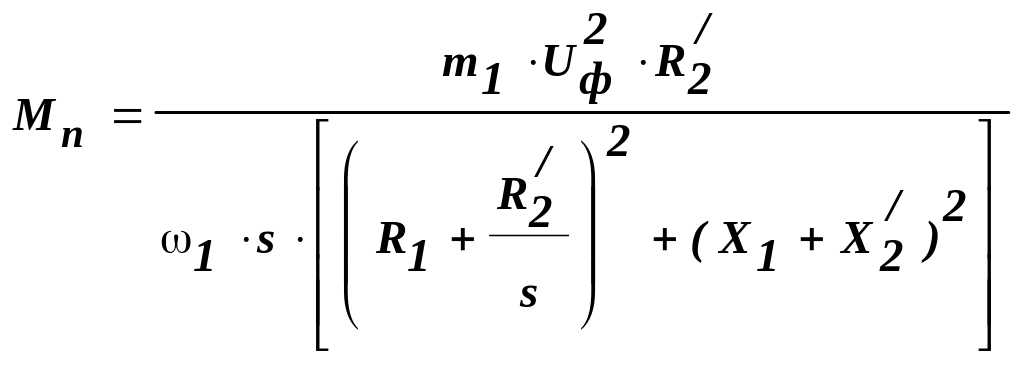Для розрахунку природної характеристики варто задаватися низкою значень ковзання s від нуля до 1,0 (з обов'язковим обліком s= s_k і s= s_н ), і знаходити для них значення М_п. Частота обертання ротора визначається для кожного значення ковзання

n = n₁ ^.(1 - s).

Розрахунки доцільно звести в табл.16.

Таблиця 16

Результати розрахунку природної механічної характеристики

s	0	sн	0,05	0,1	sk	0,2	0,4	0,6	0,8	1,0
n, об/хв
Mп, Н-м

За даними табл.16 будують графік природної механічної характеристики, що має наступні характерні точки: точку ідеального холостого ходу (n=n₁, s=0, M=0), точку номінального режиму (n=n_н, s=s_н, M=M_н), точку максимального моменту (s=s_k, M=M_max), точку пуску двигуна (n=0, s=1, M=М_nе). По вісі абсцис у масштабі відкладають значення s, а по вісі ординат – M і будують графік залежності M = f(s) .

До пункту 5. Штучну реостатну механічну характеристику АД при включенні у коло ротора опору по п.3.5 розраховують по рівнянню:

.

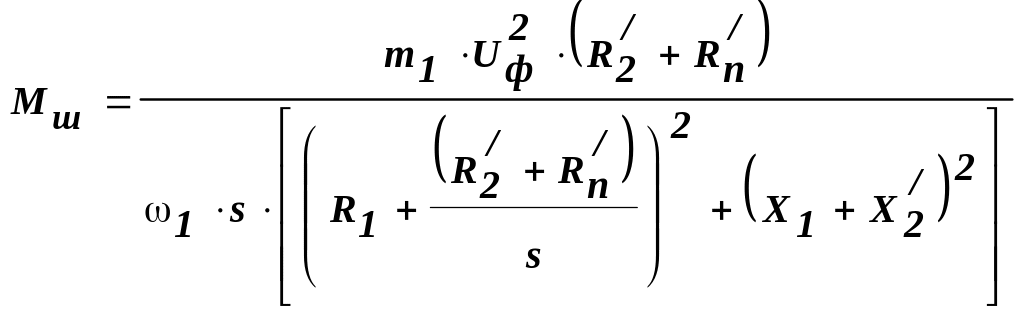Подальші розрахунки і побудови виконують аналогічно п.4.

До пункту 7. Криву I₂ = f(s) розраховують по рівнянню:

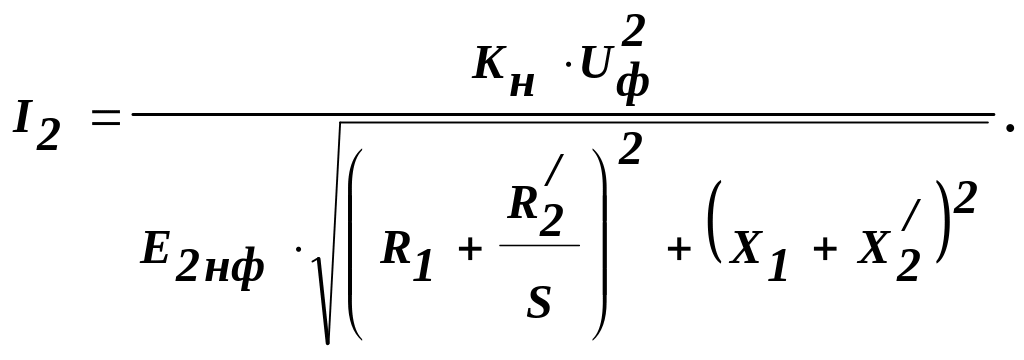
До пункту 8. Спрощений запис механічної характеристики представляється у вигляді формули Клосса:

,

де: М – значення моменту, яке відповідає значенню ковзання s.

Для розрахунку механічної характеристики варто задати ряд значень s (аналогічно п.4). Результати розрахунку доцільно звести в таблицю.

До пункту 9. У теорії ЕМ прийнято розподіл споживаної двигуном потужності з мережі при електромеханічному перетворенні енергії представляти у вигляді енергетичної діаграми. У ній потужності і втрата енергії на відповідних ділянках діаграми дорівнюють ширині цих ділянок:

Р₁ – потужність, яка підводиться до статора АД з мережі;

P_с – магнітні втрати на гистерезис і у вихрові струми в сталі магнітопровода статора;

Р_ел1 – електричні утрати потужності в обмотці статора:

Р_ел1= m₁ ^.І_1ф^{2 .} R₁;

Р_ем – електромагнітна потужність, яка передається обертовим магнітним полем ротору через повітряний зазор:

Р_ем=Р₁ - (Р_с1+Р_ел1);

Р_ел2 – електричні утрати потужності в обмотці ротора:

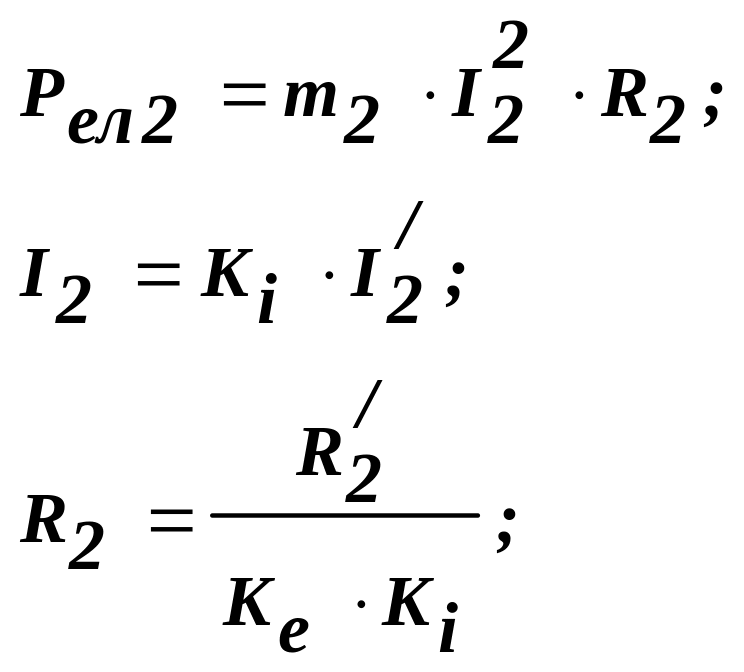
Р_мех – повна механічна потужність ротора:

Р_мех= Р_ем - Р_ел2 ;

Р_мх – механічні втрати в двигуні на тертя в підшипниках, тертя щіток об кільця, тертя ротора об повітря, включаючи втрати на вентиляцію;

Р_дод – додаткові втрати, які обумовлені зубцевою поверхнею статора і ротора:

;

Р₂ – корисна потужність на валу машини.

Втрати в сталі статора і механічні утрати приблизно рівні. Тоді:

де: – сумісні втрати потужності в двигуні,

.

З іншого боку:

=Р₁ – Р₂ .

У контрольній роботі на енергетичній діаграмі ширину ділянок, що відповідають розрахунковим потужностям, варто зображувати пропорційно цим потужностям.

Задача № 4. Асинхронний виконавчий двигун (АВД).

До пункту 3. Відносна частота обертання ротора АВД:

,

де: n – частота обертання ротора;

n₁ = 60f₁/p – синхронна частота обертання.

У випадку, якщо в завданні частота обертання, об/хв, ротора не визначена, її варто обчислити через номінальну потужність і момент:

.

До пункту 4. АВД розвиває максимальний обертальний момент при круговому обертовому магнітному полі, що має місце при пуску двигуна з ефективним коефіцієнтом сигналу . При амплітудному керуванні:

,

причому коефіцієнт трансформації можна визначити за номінальним значенням напруг U_y і U_в , що приведені в завданні.

Знаючи відносну частоту обертання ротора і номінальний обертальний момент М_н при = 1, можна визначити максимальний пусковий момент (якщо відносний момент визначити по механічній характеристиці, зображеної на рис.5), Н ^. м:

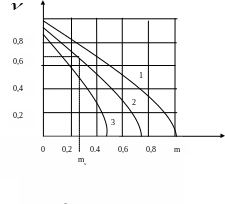
Рисунок 5.2 - Графічне визначення відносного моменту АВД по механічній характеристиці: 1) =1; 2) =0,75; 3) =0,5.

Менш точно m_н можна визначити з рівняння механічної характеристики ідеалізованого АВД:

,

тому що в ідеалізованому АВД механічні характеристики прямолінійні, у той час як у реальному двигуні вони криволінійні.

До пункту 5. При визначенні напруги рушіння варто скористатися графіками регулювальних характеристик (у відносних одиницях), приведених у рекомендованій літературі. Визначеному відносному моменту відповідає ефективний коефіцієнт сигналу.

До пункту 6. Попередньо варто визначити частоту обертання ротора при заданих умовах ( і m ), після чого відносне значення механічної потужності з відповідних графіків Р_мех = f( ) при = const знаходиться відомим способом.

До пункту 8. ККД двигуна .

Задача № 5. Синхронний двигун.

До пункту 2. Визначаються фазні значення напруги і струму синхронного двигуна. З огляду на те, що обмотки статора з'єднані зіркою, одержуємо:

;

I_ф = I_л .

Повний опір однієї фази обмотки статора, Ом:

Z=U_ф / I_ф .

Абсолютні індуктивні опори X_d , X_q визначаються через їх задані відносні значення, Ом:

Індуктивний опір розсіювання обмотки якоря , в.о.:

,

відкіля: .

Абсолютне значення, Ом:

.

До пункту 3. Обертальний момент на валу машини, Н ^. м:

,

де: Р_н – номінальна потужність, кBт;

– кутова швидкість обертання ротора.

До пункту 4. Векторну діаграму зручно будувати у відносних одиницях. Діаграму напруг перезбудженого двигуна при заданих номінальних

значеннях струму (I_фн* = 1) і напруги (U_фн* = 1) будують у наступному порядку:

1. Спочатку будують універсальну характеристику холостого ходу (рис. 6).

2. В тому ж масшстабі, як і на характеристиці холостого ходу, проводять в напрямі вісі ординат вектор напруги U і під кутом =arccos до нього — вектор випереджального фазного струму I (рис.6).

3. Під кутом 90⁰ до вектора I з кінця вектора U проводять вектор j ^.I ^.X_падіння напруги на на індуктивному опорі розсіювання. Отримаєм вектор ЕРС E_який відповідає результівному потоку _ у зазорі машини.

4. По характеристиці холостого ходу (точка А) знаходимо МРС F_, яка необхідна для створювання потока _ . Будуємо вектор F_ перпендикулярно до вектора E_До нього добудовуємо вектор F_а^/ (його визначення очевидно з рис. 6). Вектор F_а^/ співпадає за напрямом з вектором струму I і показує величину МРС реакції якоря, яка приведена до обмотки збудження.

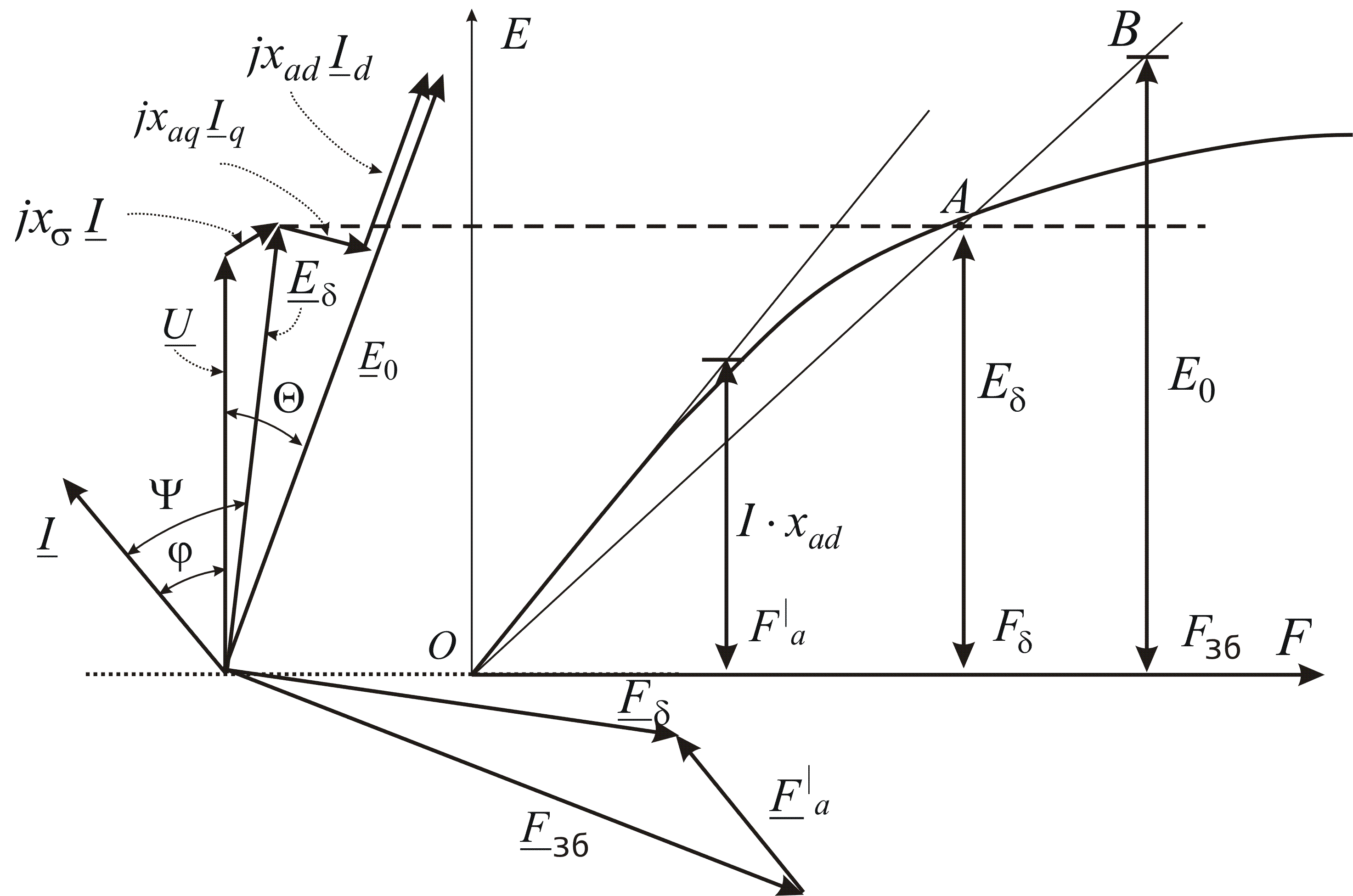
Рисунок 5.3 - Векторна діаграма перезбудженого СД

5. З початку координат до початку вектора F_а^/ проводять прямий відрізок, який відповідає МРС збудження F_зб . ПротиЕРС -E₀ випереджає його на 90⁰. Подальше будування діаграми очевидно. З векторної діаграми визначаємо кут навантаження _н для номінального момента на валу двигуна.

По основному комплексному рівнянню синхронної машини може бути побудована векторна діаграма. Однак для СД в основне рівняння замість напруги машини U треба підставити -U_c , тому що термін "напруга двигуна" звичайно не вживається. При цьому для явнополюсного СД:

-U_c = E₀ – j ^.I _d ^.X_d – j ^.I_q ^.X_q ,

де: E₀ – ЕРС обмотки якоря при холостому ході синхронної машини (при скиданні навантаження);

I_d, I_q- подовжня і поперечна складові струму якоря I:

Д о пункту 5. Під кутовою характеристикою розуміють залежність електромагнітного моменту M_ем (чи електромагнітної потужності Р_ем ) від кута між ЕРС Е₀ і напругою -U_c. Кутова характеристика повинна бути побудована для абсолютних значень М_ем у діапазоні зміни кута від 0 до 180° (рис.7).

Розрахунок М_ем проводиться по рівнянню:

,

де: ;

Е₀ – ЕРС в обмотці статора. Для її визначення використовуємо діаграму Потьє: через точку А і початок координат проводимо пряму; на вісі абсцис відкладаєм значення F_в і проводимо перпендикуляр до перетину з прямою ОА. Відрізок ВС у прийнятому масштабі і є питома ЕРС Е₀.

В рівняння моменту підставляють значення параметрів X_d і X_q для ненасиченої машини і ЕРС Е₀, визначену з векторної діаграми і

приведену до абсолютного значення (Е₀ = Е_o* U_фн). По кутовій характеристиці визначають кут навантаження , при якому двигун розвиває максимальний обертальний момент.

Рисунок 5.4 - Кутова характеристика СД: М_в - складова момента, що залежить від струму збудження; М_р - реактивна складова момента;

М_ем – сумарний електромагнітний момент

До пункту 6. Статична перевантажувальна здатність двигуна

,

причому варто обчислити для кута , визначеного по векторній діаграмі. Статична перевантажувальна здатність для СД загального призначення повинна бути не нижче 1,65. Електромагнітний момент при куті перевищує момент на валу М_2н на значення момента холостого ходу М₀, обумовленого механічними втратами в двигуні. Це дозволяє контролювати правильність побудови векторної діаграми і визначення по ній кута навантаження.

До пункту 7. Векторну діаграму (рис. 6) використовуємо також для побудування U-подібних характеристик двигуна (рис.9). При цьому будемо рахувати, що вектор F_ перпендикулярний до вектора напруги U . Тоді отримаєм наступну векторну діаграму (рис.8), де ОА_І , ОВ_І , ОС_І , ОD_I – вектори струму I, кінці яких ковзають по лінії, яка перпендикулярна до вектора напруги U; ОА_зб , ОВ_зб , ОС_зб , ОD_зб – вектори МРС F_зб*.

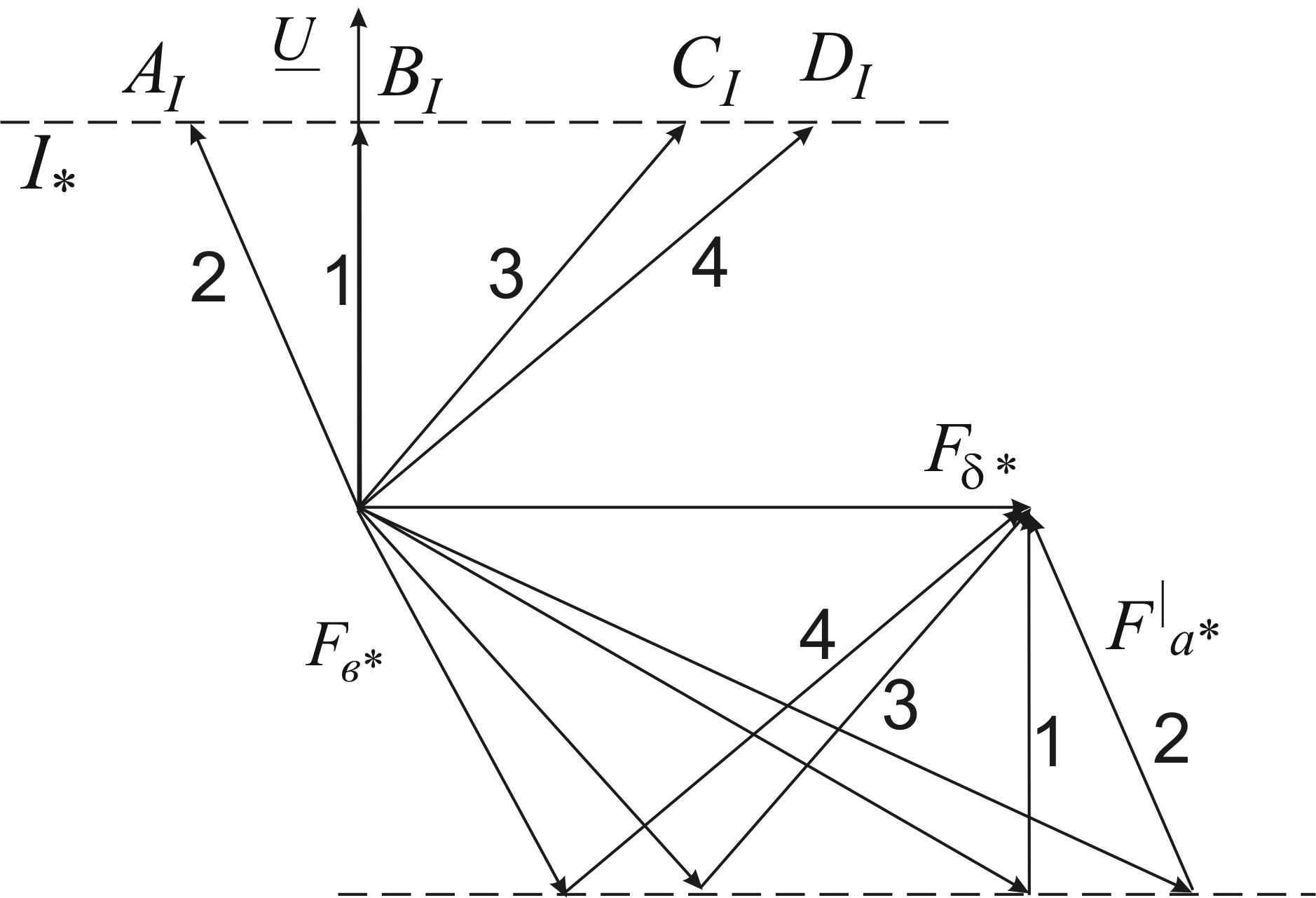
Рисунок 5.5 - До побудування V- подібних характеристик синхронного двигуна

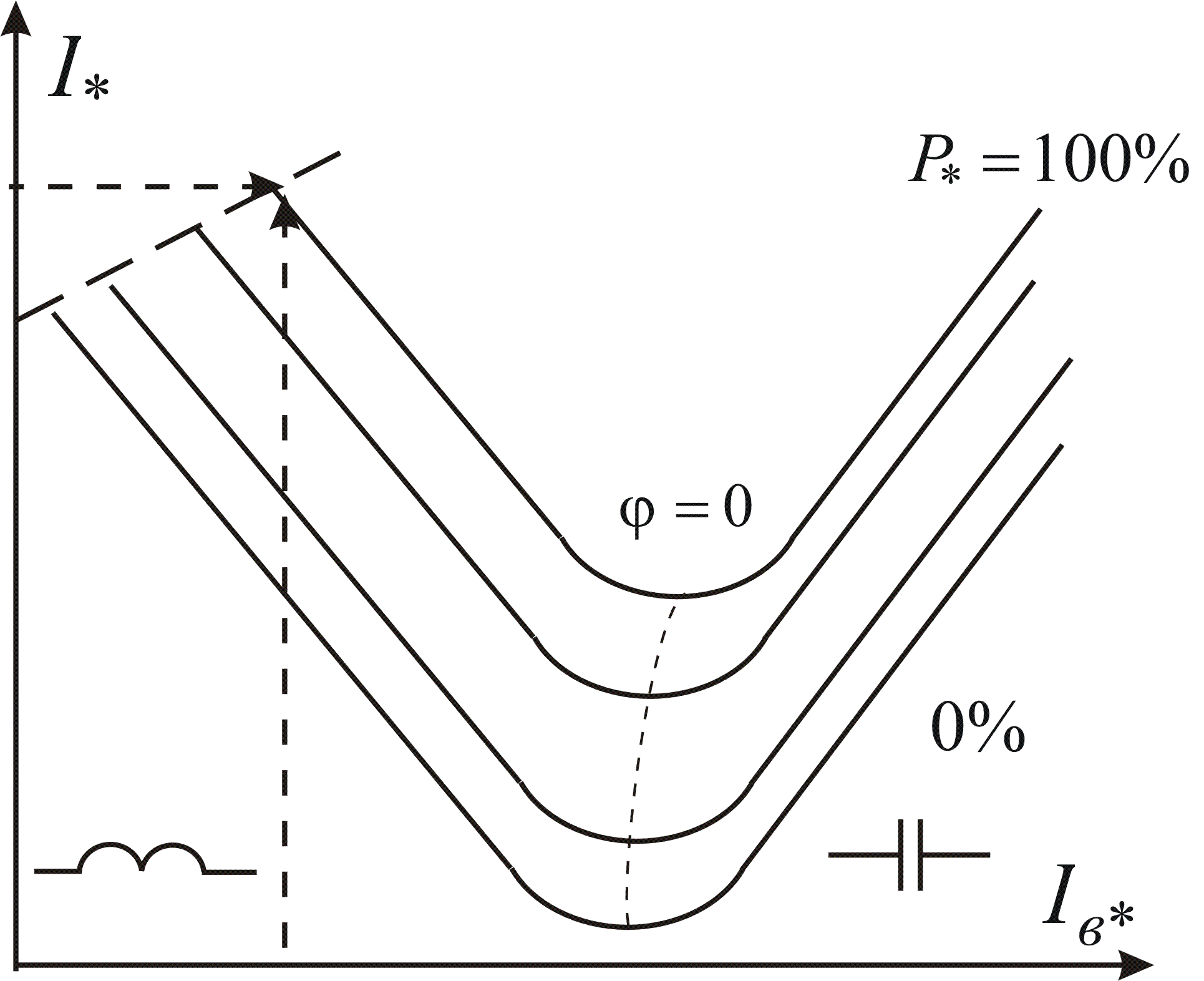
Рисунок 5.6 - V- подібні характеристики синхронного двигуна

До пункту 8. Активна потужність на затискачах двигуна:

.

Для явнополюсного СД без обліку втрат у міді обмоток статора:

.

Реактивна потужність:

, або ,

де: S – удавана (повна) потужність двигуна:

.

До пункту 10. Активна потужність, що розвивається двигуном без збудження:

.

Задача № 6. Двигун постійного струму.

До пункту 1. Для визначення струму I_н, споживаного двигуном з мережі, спочатку знаходять потужність, споживану двигуном з мережі при номінальному навантаженні:

.

Тоді:

.

Струм у колі якоря при номінальному навантаженні:

I_ан=І_н – І_зб,

де: I_зб – струм збудження обмотки паралельного збудження,

Тут: — опір обмотки збудження в нагрітому стані при 75 °С (у завданні - при 20 °С).

До пункту 2. Потужність Р_н (кВт) і момент M_2н (Н ^.м) на валу і частота обертання вала n_н (об/хв) зв'язані між собою співвідношенням:

.

Електромагнітний момент:

М = С_м ^.Ф_б ^.I_ан ,

де: С_м - постійна машини, ;

- магнітний потік.

Для визначення магнітного потоку необхідно скористатися основним рівнянням рівноваги ЕРС двигуна постійного струму:

.

Відкіля, знаючи ЕРС E_а , можна визначити магнітний потік :

,

де: - постійна машини, .

До пункту 3. Максимальний припустимий по струму якоря пусковий обертальний момент:

.

У момент пуску якір двигуна нерухомий ( n=0 ), тому струм якоря:

,

відкіля при можна визначити опір пускового реостата R_n, що забезпечує пусковий момент M_{n max} .

До пункту 4. Для двигуна з паралельним збудженням, у якого магнітний потік =const, рівняння природної механічної характеристики:

,

а графік цієї характеристики – пряма лінія, яку будують по двох точках: ідеального холостого ходу (М = 0) і номінального режиму роботи (для чого у формулу необхідно підставити електромагнітний момент М, визначений у п.2).

Значення частоти обертання n, обчислене для номінального режиму роботи, повинне збігатися з заданим значенням n_н.

До пункту 5. Рівняння штучної механічної характеристики:

.

Її будують по двох точках: ідеального холостого ходу (М = 0) і пуску двигуна ( n =0).

До пункту 6. Струм збудження зменшиться до значення

.

Для знаходження магнітного потоку варто скористатися приведеною в табл.17 залежністю магнітного потоку від струму збудження I_зб . За одиницю прийняті номінальні значення відповідно магнітного потоку і струму збудження.

Таблиця 17