4.2) Находим , , , .

- передаточная функция разомкнутой системы.

- передаточная функция замкнутой системы.

- передаточная функция по ошибке.

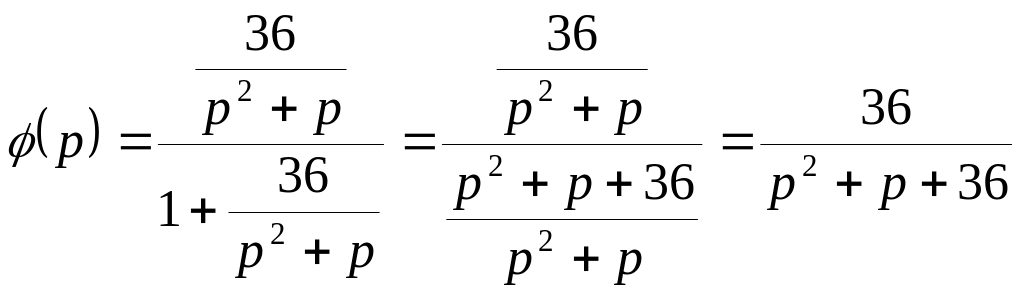
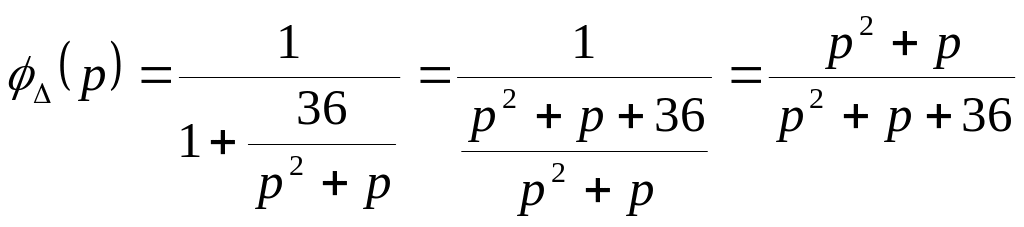
- передаточная функция по внешнему воздействию.

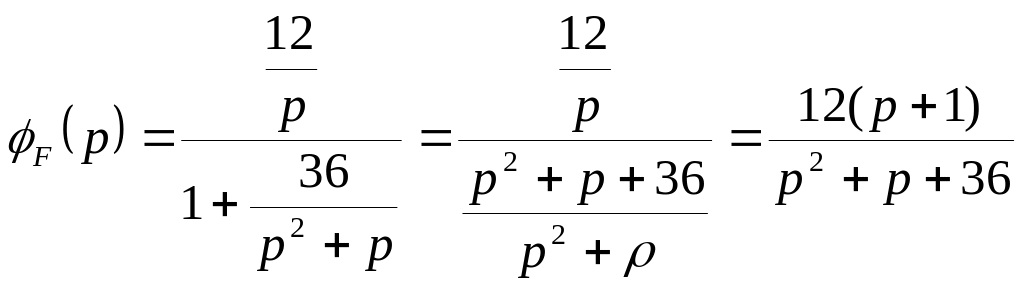
Вывод: В данном пункте были рассчитали четыре передаточных функции: функция разомкнутой системы, функция замкнутой системы, функция по ошибке, функция по внешнему воздействию.

4.3) Находим ачх и фчх для найденной . Строим лачх и лфчх.

- передаточная функция разомкнутой системы, где - общий коэффициент усиления, , постоянная времени.

- оператор дифференцирования (Лапласа)

- амплитудо-частотная характеристика (АЧХ).

- фазо-частотная характеристика (ФЧХ).

- логарифмическая амплитудо-частотная характеристика (ЛАЧХ).

Построим найденные характеристики:

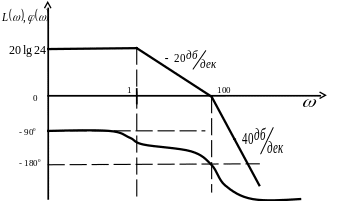
Рисунок 13 - ЛАЧХ и ЛФЧХ для

Вывод: Данное звено представляет собой последовательное соединение двух апериодических звеньев 1-го порядка. Сдвиг фазы передаточной функции равен –180⁰. ЛАЧХ отклоняется сначала вверх на , а затем вниз на .

4.4) Исследуем на устойчивость по критериям: Гурвица, Михайлова и Найквиста.

- передаточная функция разомкнутой системы.

Запишем эту функцию в виде характеристического уравнения:

, т. е.

Критерий Михайлова:

Представим это уравнение в виде характеристического вектора ,

который получается заменой - оператор дифференцирования (Лапласа):

, откуда получаем

- действительная составляющая.

- мнимая составляющая.

Построим график:

0	0	24
1	1	23.99
10	10	23.9
100	100	23
1000	1000	14
10000	10000	-76

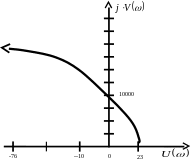
Рисунок 14 - Практическое изображение характеристического вектора

Так как характерный вектор САУ при изменении частоты от 0 до выходя из , проходит 2 квадранта против часовой стрелки, описывающая расходящуюся спираль, то система устойчива.

Критерий Гурвица:

Из характеристического уравнения составляем, по определённым правилам, основной определитель :

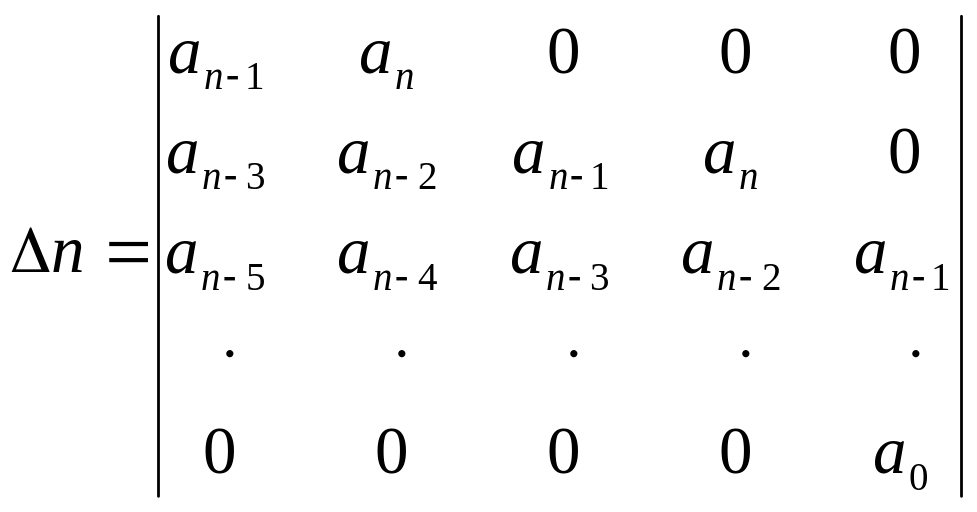
а - при , , 0, определитель Гурвица получается из основного определителя путём вычёркивания соответствующих строк и столбцов.

Составляем определитель второго порядка:

б - , так как 0, то по данному критерию система устойчива.

Критерий Найквиста:

Построим график, подставляя в ранее найденные и для :

1	70.7	-45.6
2	44.7	-64.6
5	31.6	-73.3
10	19.6	-81.5
20	10.9	-88.8
50	4.9	81.6
100	3.2	75.2

Рисунок 15 - Теоретическая АЧХ разомкнутой системы на комплексной плоскости

Из графика видно, что АЧХ разомкнутой системы не охватывает на плоскости точку с координатой , то система по данному критерию устойчива.

- 23 -

Вывод: Данная функция является устойчивой. Это подтвердили три критерия: Гурвица, Михайлова и Найквиста.

4.5) Определяем точность структурной схемы. Находим общую ошибку.

а) Ищем ошибку по задающему воздействию:

Воспользуемся - передаточная функция по ошибке.

В этой функции числитель делим на знаменатель:

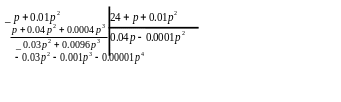
Получаем ; - постоянные коэффициента ошибок.

Исходя из исходных данных: - задающее воздействие.

- ошибка по задающему воздействию.

б) Ищем ошибку по возмущающему воздействию:

Воспользуемся - передаточная функция по внешнему воздействию.

В этой функции числитель делим на знаменатель:

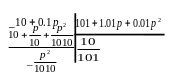
Получаем - постоянная коэффициента ошибок.

Исходя из исходных данных: - возмущающее воздействие.

- ошибка по возмущающему воздействию.

в) Ищем общую ошибку:

Вывод: Определена точность работы системы. Найдена ошибка по задающему воздействию, по возмущению и общая ошибка.