Пензенский государственный университет Институт систем управления и информационной безопасности Кафедра «аиус»

Курсовой проект на тему: «Исследование линейных систем автоматического

управления»

Содержание курсового проекта

1. Реферат ……………………………………………………………………….. 3

2. Задание на курсовой проект ……………………………………………….. 4

3. Теоретическая часть ………………………………………………………... 5

4. Основная часть:

4.1 Находим АЧХ и ФЧХ для и . Строим ЛАЧХ и ЛФЧХ…. 14

4.2 Находим , , , ………………………………………… 19

4.3 Находим АЧХ и ФЧХ для найденной . Строим ЛАЧХ и ЛФЧХ……………………………………………………………………….. 20

4.4 Исследуем на устойчивость по критериям: Гурвица,

Михайлова и Найквиста………………………………………………… 22

4.5 Определяем точность структурной схемы. Находим общую

ошибку……………………………………………………………………... 24

4.6 Для рассчитаем переходную характеристику и построим её…………………………………………………………………………… 25

4.7 Определяем по графику основные показатели качества…………… 27

5. Заключение…………………………………………………………………... 29

6. Список используемой литературы……………………………………….. 30

6. Приложение А.................................................................................................. 31

РЕФЕРАТ

Курсовой проект содержит 31 страниц, 17 рисунков.

ПЕРЕДАТОЧНЫЕ ФУНКЦИИ и , ЗАДАЮЩЕЕ ВОЗДЕЙСТВИЕ , ВОЗМУЩАЮЩЕЕ ВОЗДЕЙСТВИЕ .

Целью работы является исследование линейных систем автоматического управления.

В процессе работы произведен расчет соответствующих передаточных функций (нахождение и построение АЧХ, ФЧХ, ЛАЧХ), проведено исследование на устойчивость по критериям Гурвица, Михайлова и Найквиста, определены точность работы структурной схемы и общая ошибка, найдены основные показатели качества, а так же даны обоснования и выводы.

В результате работы была исследована исходная линейная сау.

3. Теоретическая часть

Типовым динамическим звеном САУ является составная часть системы, которая описывается дифференциальным уравнением не выше второго порядка. Звено, как правило, имеет один вход и один выход. По динамическим свойствам типовые звенья делятся на следующие разновидности: позиционные, дифференцирующие и интегрирующие. Позиционными звеньями являются такие звенья, у которых в установившемся режиме наблюдается линейная зависимость между входными и выходными сигналами. При постоянном уровне входного сигнала сигнал на выходе также стремится к постоянному значению. Дифференцирующими являются такие звенья, у которых в установившемся режиме выходной сигнал пропорционален производной по времени от входного сигнала. Интегрирующими являются такие звенья, у которых выходной сигнал пропорционален интегралу по времени от входного сигнала. Звено считается заданным и определенным, если известна его передаточная функция или дифференциальное уравнение. Кроме того, звенья имеют временные и частотные характеристики. Наличие нулевых корней в числителе или знаменателе ПФ типовых звеньев - это признак для разбиения последних на три группы:

Позиционные звенья: 1, 2, 3, 4, 5, - не имеют нулевых корней, и, следовательно, в области низких частот (т.е. в установившемся режиме), имеют коэффициент передачи равный k. Интегрирующие звенья: 6, 7, 8, - имеют нулевой корень-полюс, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к бесконечности. Дифференцирующие звенья: 9, 10 - имеют нулевой корень-ноль, и, следовательно, в области низких частот, имеют коэффициент передачи, стремящийся к нулю.

Частотные характеристики.

В условиях реальной эксплуатации САУ часто возникает необходимость определить реакцию на периодические сигналы, т.е. определить сигнал на выходе САУ, если на один из входов подается периодически сигнал гармонической формы.

Решение этой задачи возможно получить путем использования частотных характеристик. Частотные характеристики могут быть получены экспериментальным или аналитическим путем. При аналитическом определении исходным моментом является одна из передаточных функций САУ (по управлению или по возмущению). Возможно также определение частотных характеристик исходя из передаточных функций разомкнутой системы и передаточной функции по ошибке. Если задана передаточная Функция W(р), то путём подставки p=jω получаем частотную передаточную функцию W(jω), которая является комплексным выражением т.е. W(jω)=U(ω)+jV(ω), где U(ω) - вещественная составляющая , а V(ω) - мнимая составляющая. Частотная передаточная функция может быть представлена в показательной форме:

W(jω)=A(ω)e^jφ(ω)

, где - модуль; 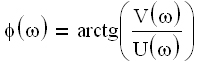- аргумент частотной передаточной функции.

Функция A(ω), представленная при изменении частоты от 0 до получило название амплитудной частотной характеристики (АЧХ). Функция Φ(ω), представленная при изменении частоты от 0 до называется фазовой частотной характеристикой (ФЧХ). Таким образом, дифференциальное уравнение движения системы связывает входной и выходной 1000 сигналы (т.е. функции времени), ПФ связывает изображения Лапласа тех же сигналов, а частотная ПФ связывает их спектры. Частотная передаточная функция W(jω) может быть представлена на комплексной плоскости. Графическое отображение для всех частот спектра отношений выходного сигнала САУ к входному, представленных в комплексной форме будет представлять собой амплитудно-фазовую частотную характеристику (АФЧХ) или годограф Найквиста. Величина отрезка от начала координат до каждой точки годографа показывает во сколько раз на данной частоте выходной сигнал больше входного - АЧХ, а сдвиг фазы между сигналами определяется углом до упомянутого отрезка - ФЧХ. При этом отрицательный фазовый сдвиг представляется вращением вектора на комплексной плоскости по часовой стрелке относительно вещественной положительной оси, а положительный фазовый сдвиг представляется вращением против часовой стрелки. Для упрощения графического представления частотных характеристик, а также для облегчения анализа процессов в частотных областях используются логарифмические частотные характеристики: логарифмическая амплитудная частотная характеристика (л.а.ч.х.) и логарифмическая фазовая частотная характеристика (л.ф.ч.х.).