7.Классическая задача потребления. Функция индивидуального спроса.

Пусть денежный доход потребителя равен M. Вектор цен обозначим через P=(p₁,p₂,…,p_n), где p_j – цена товара вида j. Допустимое мно-во наборов для потребителя удовлетворяет неравенствам: . Граница этого мн-ва, вдоль которого называется бюджетной линией, а само равенство бюджетным ограничением.

Классическая задача потребления заключается в выборе «самого предпочтительного» набора товаров из допустимого мн-ва

Функция индивидуального спроса. Количество спрашиваемого индивидом блага зависит от: цены данного блага (Pi), цен других благ (Pj) и бюджета индивида (М):

Г рафик функции индивидуального спроса. Отрицательный наклон линии спроса отображает закон спроса. Влияние других аргументов функции QiD на количество спрашиваемого блага выражается в соответствующем сдвиге линии спроса. Так, при увеличении бюджета потребитель по каждой цене будет спрашивать большее количество, т.е. его кривая спроса сдвинется вправо. В связи с этим важно различать изменение объема спроса на каждое благо (перемещение по линии D) и изменение спроса (сдвиг линии D). Когда все факторы, определяющие объем спроса на благо, кроме его цены, постоянны, функция спроса принимает частный вид функции спроса по цене: Q = Q(P).

Допустим, что индивид потребляет лишь три вида благ (А,В,С); их воздействие на уровень полезности отображается функцией (1):

Бюджет индивида равен М, тогда его бюджетное ограничение задается следующим равенством (2): M = P_AQ_A + P_BQ_B + P_CQ_C

Чтобы узнать, какая структура покупок обеспечивает потребителю максимум полезности, нужно максимизировать функцию Лагранжа (3):

Условие ее максимизации следующее (4):

Так как в левой части равенств (4) стоит предельная полезность каждого из благ, то легко заметить, что условие максимизации функции Лагранжа представляет В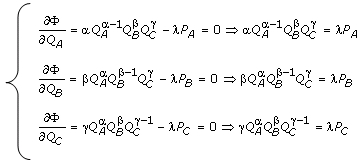 торой закон Госсена: максимум полезности обеспечивает такая структура покупок, при которой отношение предельной полезности (u) блага к его цене (Р) одинаково для всех благ:

Разделив первое равенство поочередно на второе и третье равенства, после преобразований получим (5):

Подставив значения (5) в бюджетное уравнение (2), получим функцию спроса индивида на благо А:

Заменив в выражениях (5) объем спроса функцией спроса на благо А, получим функции спроса на два других блага (6):

Обратим внимание на то, что среди аргументов функций спроса на каждое благо не оказалось цен других благ, т.е. объем спроса на одно благо не зависит от цен других благ. Такой результат связан с особым типом функции полезности индивида в рассмотренном случае. Если предпочтения потребителя отображаются функцией полезности типа (1), то объем спроса на благо зависит только от его цены и величины бюджета; цены других благ не влияют на объем спроса данного блага, так как в этом случае вкусы потребителя таковы, что он на каждый вид благ выделяет фиксированную долю бюджета. Эта доля определяется как отношение показателя степени, к сумме всех показателей степени функции полезности.

Таким образом, вид функции полезности определяет характер зависимости объема спроса потребителя от его бюджета и цен благ.