НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

им. Р.Е. АЛЕКСЕЕВА

Факультет автоматики и электромеханики

Кафедра теоретической и общей электротехники

ВЕКТОРНЫЕ ТОПОГРАФИЧЕСКИЕ ДИАГРАММЫ В ЦЕПЯХ

ТРЕХФАЗНОГО ПЕРЕМЕННОГО ТОКА

Представил Башев А.А.

Н.Новгород, 2010.

ЦЕПИ ТРЁХФАЗНОГО ПЕРЕМЕННОГО ТОКА

§ 1. Основные понятия и определения, относящиеся к трёхфазному току

Многофазной системой электрических цепей называют совокупность электрических цепей, в которых действуют синусоидальные э.д.с одной и той же частоты, сдвинутые друг относительно друга по фазе и создаваемые общим источником электрической энергии. Отдельные электрические цепи, входящие в состав многофазной электрической цепи, называют фазами. Число фаз многофазной системы будем обозначать через m.

В частности, при m=3 имеем трехфазную цепь.

Источником трёхфазной системы э.д.с. служит трёхфазный генератор.

Под трёхфазной симметричной системой э.д.с. понимают совокупность трёх синусоидальных э.д.с. одинаковой частоты и амплитуды, сдвинутых относительно друг друга на (рис. 1).

Мгновенные значения трёхфазной симметричной системы э.д.с. генератора можно записать так:

Если начальную фазу э.д.с. принять равной нулю, то

В символической форме записи для действующих значений э.д.с. имеем

если вектор направить по оси вещественных чисел (рис. 1, б).

На рис. 1, а представлена временная развёртка мгновенных значений фазных э.д.с. генератора , и , а на рис. 1, б изображена соответственно векторная диаграмма действующих значений этих э.д.с. на комплексной плоскости.

Рис. 1.

Генератор или питающая обмотка трансформатора могут быть соединены звездой или треугольником. Однако соединение обмоток генератора треугольником, как правило, не применяют. При соединении звездой с нейтральным проводом можно получить два напряжения.

Приёмники (нагрузку) соединяют и звездой, и треугольником независимо от способа соединения обмоток генератора или трансформатора.

Фазы генератора и приёмника имеют по два вывода, которые называют “началами” и “концами”. За начало обмотки генератора принимают тот вывод, к которому напрвлена (имеется в виду положительное направление) э.д.с. Начала фаз генератора обозначим через А, В, С, концы – через X, Y, Z и соответственно у приёмника – через a, b, c, x, y, z. Общие точки при соединении фаз генератора (рис. 2) и приёмника (рис. 4, 5) звездой называются нейтральными (нулевыми) и обозначаются соответственно О и O’, а соединяющий их провод – нейтральным (нулевым) проводом. Провода, соединяющие начала фаз генератора и приёмника, называют линейными проводами.

Положительные направления тока в линейных проводах обычно выбирают от генератора к приёмнику, в нулевом проводе – от нулевой точки О’ приёмника к нулевой точке О генератора (рис. 2).

Напряжения на зажимах фаз генератора и приёмника называются фазными напряжениями и соответственно обозначаются: для генератора (рис. 2) , для приёмника при соединении звездой (рис. 4, 5) , при соединении треугольником (рис. 6) и .

Напряжения между линейными проводами называются линейными напряжениями и обозначаются через , или и .

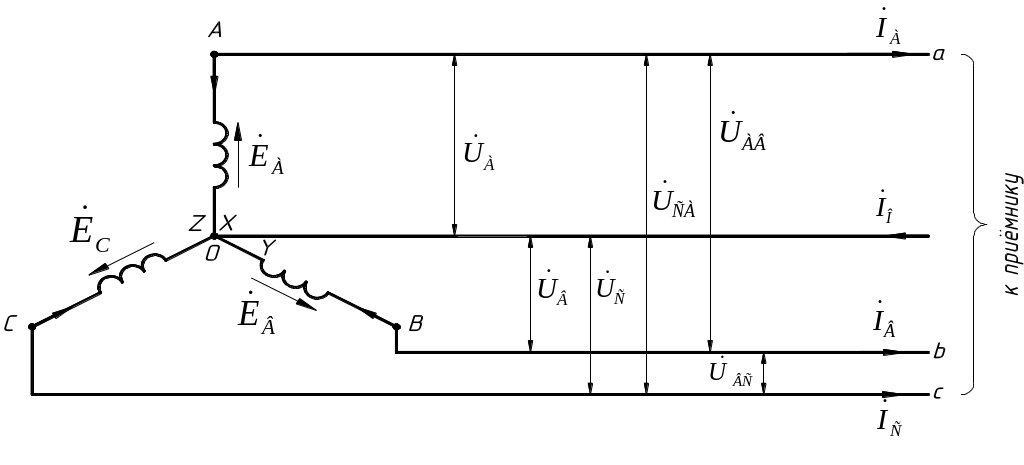
Рис. 2.

Для получения соотношений между фазными и линейными напряжениями генератора запишем их мгновенные значения через потенциалы соответствующих начал и концов фаз генератора; потенциалы концов обмоток генератора (нулевой точки О) принимаем равными нулю.

и

Переходя от мгновенных значений к действующим, в символической форме получим

(1)

На рис. 3, а показано геометрическое построение линейных напряжений, как разность векторов фазных напряжений.

Переместив полученные векторы линейных напряжений параллельно самим себе так, чтобы они образовали замкнутый треугольник, получим топографическую диаграмму напряжений (рис. 3, б). Из неё видно, что первый индекс у линейного напряжения показывает, в какую сторону направлен этот вектор. Согласно выражениям (1) и рис. 3, б векторы линейных напряжений всегда образуют замкнутый треугольник, так как их сумма равна нулю.

Поскольку мощность приёмников обычно значительно меньше мощности источника питания, то линейные напряжения можно считать неизменными, независящими от нагрузки приёмников.

Если пренебречь сопротивлениями линейных проводов или учесть их в сопротивлении фаз приёмника, то можно считать, что зажимы a, b, c приёмников имеют одинаковые потенциалы с соответствующими зажимами A, B, C источника питания.

На рис. 4, 5, 6 показаны соединения приёмников звездой (четырёхпроводная и трёхпроводная цепи) и треугольником.

Рис. 3.

При соединении приёмника звездой в случае симметричной нагрузки фазные напряжения одинаковы по величине, и нулевая точка О’ приёмника (рис. 7, б) имеет потенциал, равный нулю и совпадает с нулевой точкой О источника питания, положение которой, как и положение точек A, B, C, не зависит от нагрузки. В этом случае применяется трёхпроводная цепь и нулевой провод не требуется. К этой группе приёмников относятся трёхфазные электродвигатели.

При неравномерной нагрузке фаз, когда , нарушается симметрия фазных токов, в результате чего напряжения на отдельных фазах нагрузки могут значительно отличаться друг от друга по величине (например, при отключении нагрузки одной из фаз). Поэтому при несимметричной нагрузке фаз применяется четырёхпроводная цепь с нулевым проводом. Обрыв нулевого провода недопустим, вследствие чего в нулевом проводе никогда не устанавливают предохранитель.

Чем меньше сопротивление нулевого провода, тем ближе по величине потенциалы нулевых точек О и О’.

Необходимо стремиться к более равномерной нагрузке в фазах, чтобы ток в нулевом проводе был незначительным. Тогда падение напряжения в нулевом

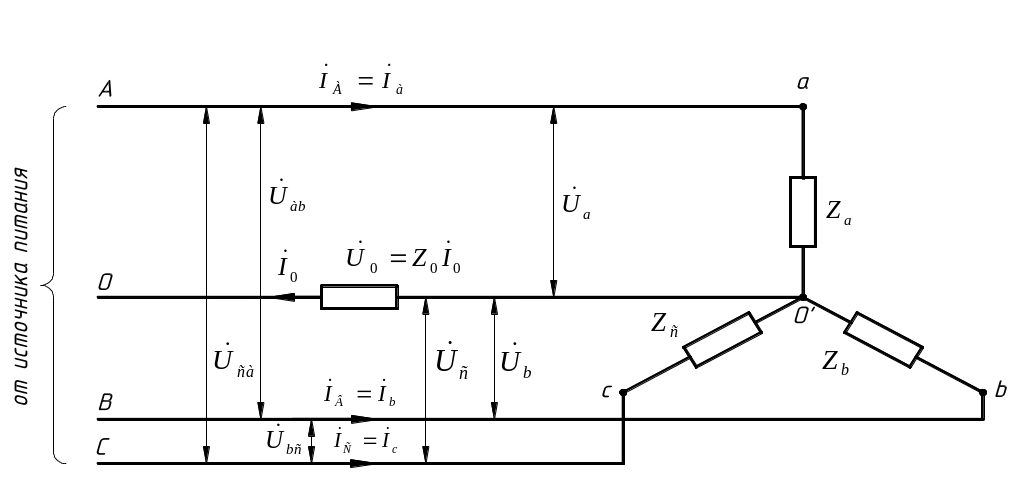Рис. 4.

проводе, называемое узловым напряжением, будет малой величиной и приёмники во всех фазах будут находиться под одинаковым напряжением .

Рис. 5.

Для симметричной трёхфазной цепи, соединённой звездой, справедливо соотношение между линейными и фазными напряжениями . Токи линейные и фазные будут равны между собой .

При соединении приёмника треугольником фазные напряжения равны линейным напряжениям , а токи линейные и фазные различны. Для получения симметричных соотношений между линейными и фазными токами следует, выбирать их положительные направления единообразно, а именно, считая по-прежнему (как и при соединении звездой) положительными направления линейных токов от источника питания к приёмнику, положительные направления для фазных токов – по направлению обхода контура

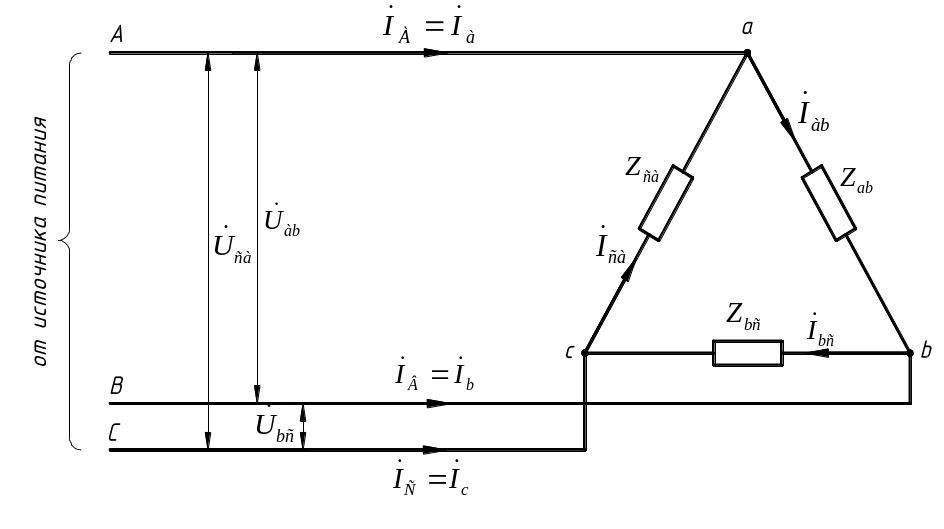
Рис. 6.

треугольника, например, по часовой стрелке (рис. 6). Тогда по первому закону Кирхгофа для мгновенных значений токов относительно узла а можем написать

, откуда

аналогично

и .

Для действующих значений в символической форме:

, и .

то есть линейные токи равны разности соответствующих , протекающих по фазам приёмника.

Из полученных соотношений следует, что сумма линейных токов всегда равна нулю.

, или .

При симметричной трёхфазной цепи, соединённой треугольником, .

Расчёт трёхфазной цепи обычно сводится к определению токов , протекающим по фазам приёмника

,

где – фазное напряжение приёмника.

– сопротивление фазы приёмника.

Фазное напряжение приёмника определяется в зависимости от симметрии системы и схемы соединения.

Если система напряжений источника питания и нагрузка симметричны, то расчёт ведётся на любую из трёх фаз.

Если система напряжений источника питания и нагрузка несимметричны, то токи в каждой из фаз также несимметричны.

Ниже приводятся формулы для определения фазных напряжений , и при отсутствии магнитной связи между фазами приёмника и соединении его звездой.

В случае четырёхпроводной трёхфазной системы, когда заданы фазные напряжения , , источника питания и сопротивления , , , фаз приёмника и нулевого провода (или соответственно проводимости , , , ).

где – узловое напряжение.

В случае трёхпроводной трёхфазной системы, когда заданы линейные напряжения источника питания и сопротивления фаз приёмника

; ; .

Расчёт магнитосвязанных трёхфазных цепей производится аналогично расчёту магнитосвязанных цепей однофазного синусоидального тока .

Ниже рассмотрены наиболее характерные режимы работы в цепях трёхфазного тока при соединении приёмника звездой с нулевым проводом и без него, а также при соединении треугольником.