4.6 Анализ речи на основе линейного предсказания

Анализ речи на основе линейного предсказания базируется на использовании модели речевого сигнала, представленной на рис.4.1, Основная задача метода состоит в том, чтобы по наблюдениям последовательности отсчетов речевого сигнала s[n] определить коэффициенты a[k] цифрового фильтра указанной модели [14,15,17].

Найденные значения коэффициентов, которые называют коэффициентами линейного предиктивного кодирования (ЛПК), могут применяться при определении частоты основного тона, при кодировании речи в соответствии с АДИКМ, в задачах распознавания и синтеза речи.

Главное допущение метода линейного предсказания состоит в том, что речевой отсчет на выходе голосового тракта s[n] может быть предсказан по линейной комбинации своих предыдущих значений и значению сигнала и [п]

где G - коэффициент усиления; Р - порядок линейного предсказателя. Е этом случае передаточная функция предсказателя соответствует передаточной функции рекурсивного фильтра

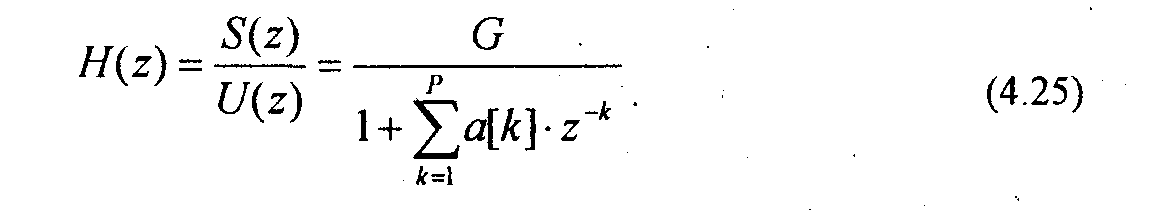
Определение коэффициентов линейного предсказания речи имеет прямое отношение к спектральному анализу, основанному на использовании АР-модели. Вместе с тем, использование модели, приведенной на рис.4.1, вносит некоторую специфику. Поэтому рассмотрим оценивание ЛПК речи подробнее. Так как отсчеты возбуждающей последовательности и[п] неизвестны, то последовательность s[n] может быть предсказана только по своим пре­дыдущим значениям

Ошибка предсказания в этом случае будет равна

Определим коэффициенты a[k] таким образом, чтобы сумма квадратов ошибок предсказания была минимальна

Для минимизации (4.28) найдем частные производные (4.28) по a[k] и приравняем их к нулю

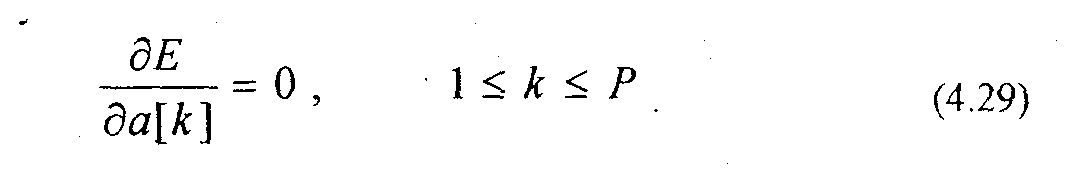
В результате получим систему уравнений

где a[k] -оценки коэффициентов a[k].

В общем случае суммирование в (4.30) должно выполняться по всем значениям п. Однако на практике суммирование по я в уравнении (4.30) вы­полняют для ограниченного числа отсчетов s[n], чтобы соблюдалось усло­вие стационарности s[n]. Для этого ограничивают последовательность s[n] с помощью окна w[n]

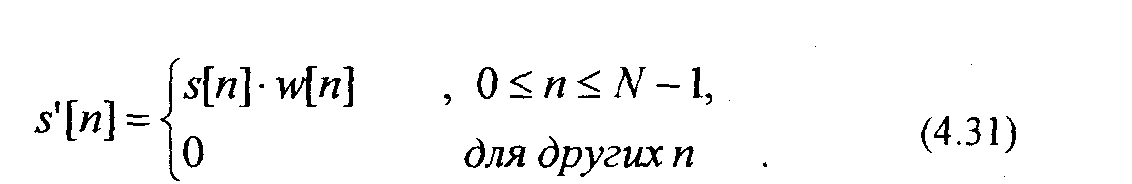
Тогда систему уравнений (4.30) можно переписать в виде

автокорреляционная функция ограниченной последовательности s'[n].

Так как автокорреляционная функция является четной, т.е. г[от]=г[-/п],

то (4.32) можно записать в матричной форме ;

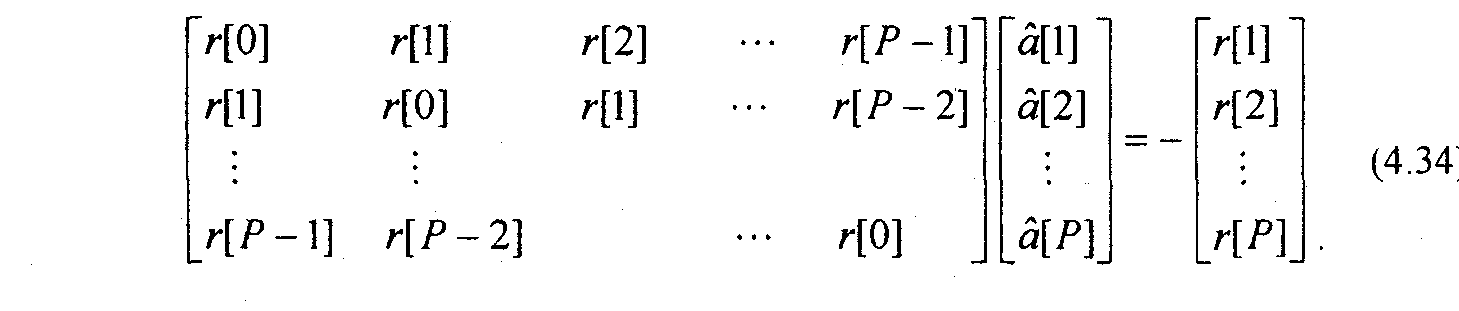
Матричное уравнение (4.34) имеет структуру аналогичную уравнению (2.35) и может быть решено с помощью рекурсивного алгоритма Левинсона - Дарбина. В соответствии с этим алгоритмом решение для предсказателя т-го порядка получается на основе решения для предсказателя т-\ порядка. Формально алгоритм определяется следующими соотношениями 4,14,15,171:

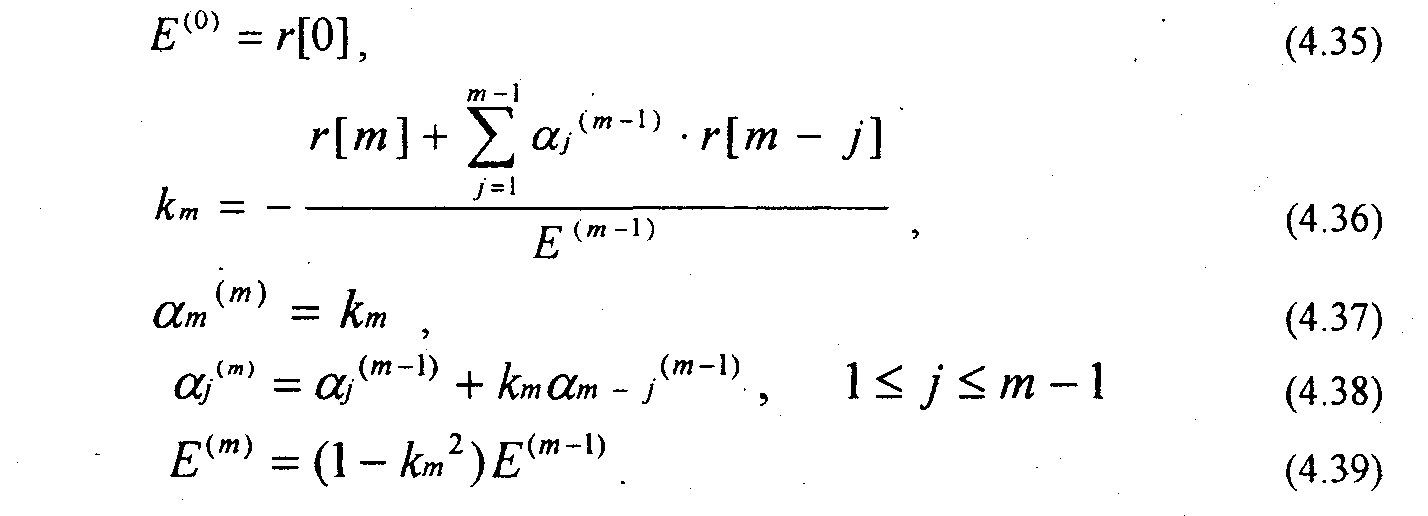
Уравнения (4.35 - 4.39) решаются рекурсивно для т=1, 2, ...,Р: Отметим, что для от=1 параметр а^ = k\ = r[l]/r[0] и. Е^ = (1 - k^)r[0]. Для конечного решения порядка Р коэффициенты линейного предсказания будут равны

Коэффициенты km называются коэффициентами отражения. Е представляет сумму квадратов ошибки предсказания для предсказателя т-го порядка. Автокорреляционную функцию последовательности s'[n] оцени­вают на основе соотношения:

Линейное предсказание речи можно использовать для определения частотной характеристики голосового тракта

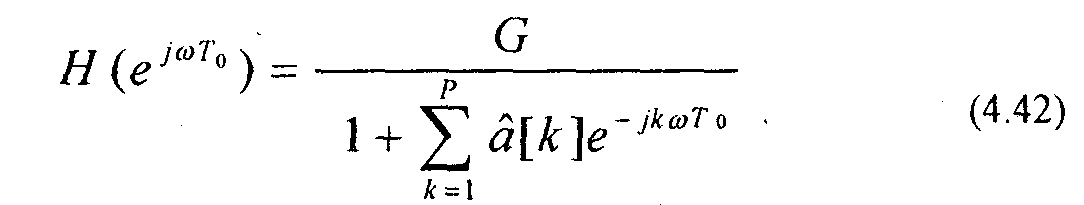
Данная характеристика соответствует медленно меняющейся составляющей кратковременного спектра речевого сигнала. На рис. 4.10 представлен кратковременный спектр речевого сигнала и АЧХ голосового тракта, вычисленная с помощью (4.42). Порядок фильтра Р=28. На графике АЧХ хорошо представлены форманты.

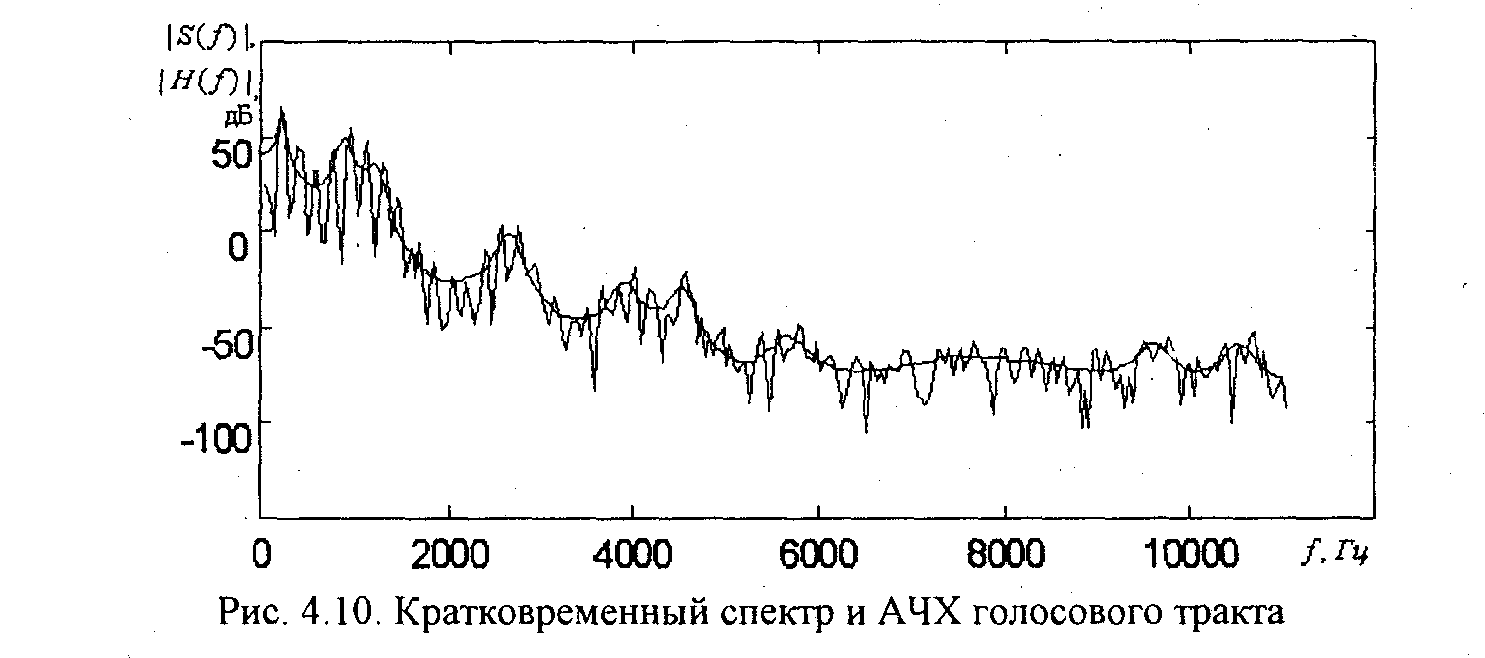
Недостатком рассмотренного метода определения ЛПК является необходимость вычисления матрицы автокорреляций. Кроме этого, если вычисленные значения ЛПК применяются при синтезе речи в соответствии со схемой, показанной на рис.4.1, то возникают вопросы обеспечения устойчивости цифрового рекурсивного фильтра высокого порядка.

В настоящее время развит класс методов, которые оценивают ЛПК непосредственно по отсчетам последовательности s[n] и которые лучше приспособлены для решения задач синтеза речи. Эти методы базируются на использовании лестничного фильтра [17].

Рассмотрим алгоритм Левинсона-Дарбина. Параметры aii представляют коэффициенты предсказывающего фильтра т-го порядка. Определим передаточную функцию

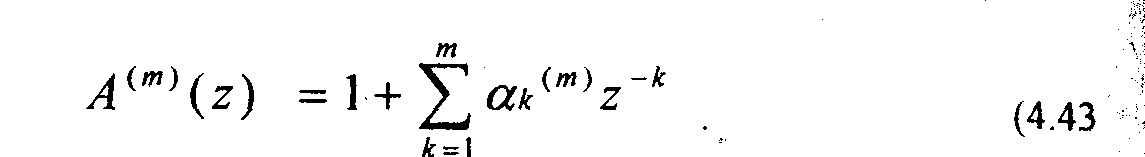
Эта передаточная функция соответствует инверсному фильтру и являете» '^j обратной по отношению к передаточной функции предсказателя (4.25). Е ' соответствии с (4.27) на вход инверсного фильтра поступает речевой сигнал s[n], а на выходе формируется ошибка предсказания. Ошибка предсказания;

для предсказателя т-го порядка будет равна

Найдем z-преобразование (4.44). Тогда

Подставив (4.38) в (4.43), получим

Отсюда получаем рекурсивное выражение для вычисления A''"'\z)

Подставляя (4.47) в (4.45), получаем выражение для ошибки предсказания

Первый член в (4.48) соответствует ошибке предсказания для предсказателя (т-1 )-го порядка. Для второго члена в (4.48) без km введем обозначение

Выражению (4.49) соответствует разностное уравнение

Данное уравнение соответствует обратному предсказанию, т.е. оно позволяет предсказать отсчет по предстоящим отсчетам s[(n-m)+k] и (рис.4.11).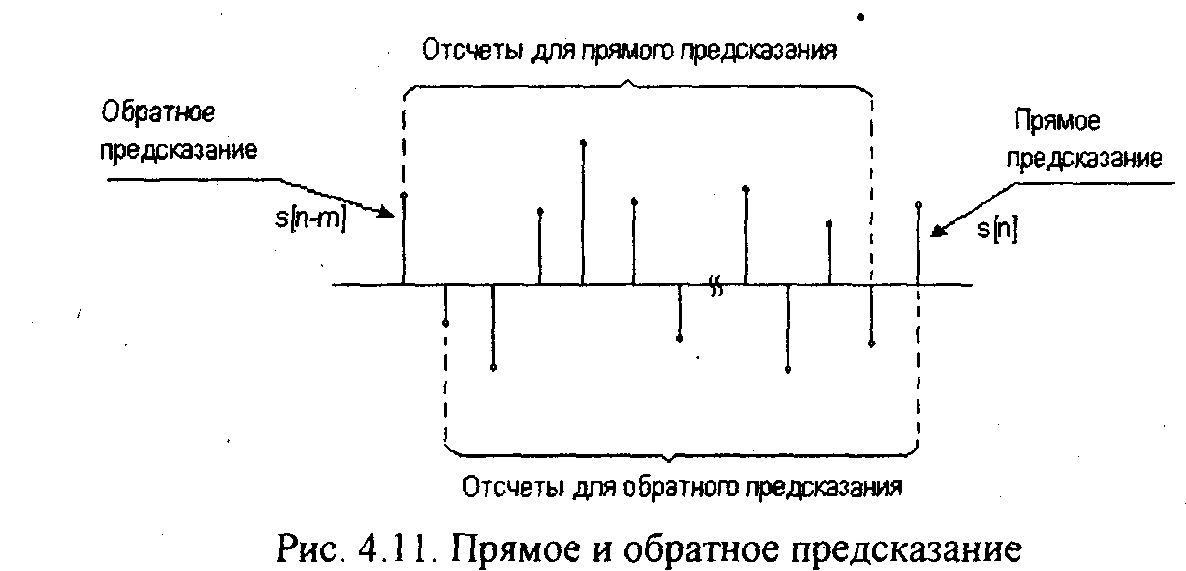

Сравнивая (4.50) и (4.44), отмечаем, что b"'[n] соответствует ошибке обратного предсказания. Таким образом, ошибка прямого предсказания (4.48) может быть представлена в виде

Выполнив аналогичные преобразования для (4.50), получим симметричное выражение для ошибки обратного предсказания

Уравнения (4.51) и (4.52) являются рекуррентными и определяют ошибки предсказаний для предсказателя т-го порядка через ошибки предсказания для предсказателя (m-l)-ro порядка. При этом для предсказателя нулевого порядка

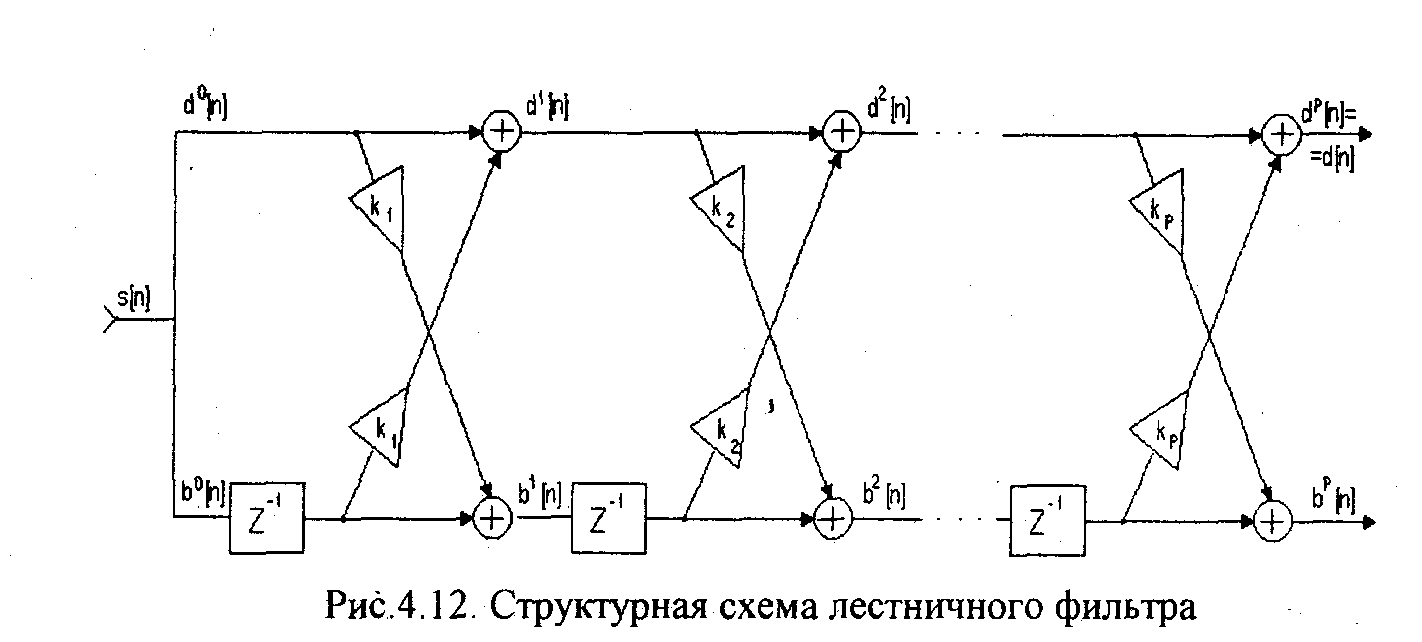
Уравнения (4.51) и (4.52) соответствуют лестничному фильтру и могут быть представлены в виде структурной схемы, изображенной на рис.4.12.

Коэффициенты отражения km могут вычисляться в соответствии с уравнениями (4.35 - 4.39). Однако имеется и иная возможность. В [11,36] показано, что коэффициенты отражений можно вычислять через ошибки предсказания d"[n\ и &"*[«] в соответствии с соотношением

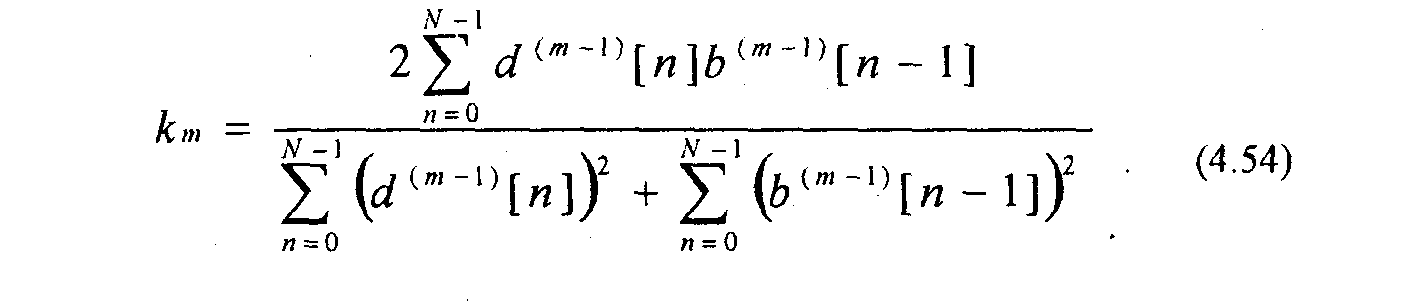
Выражение (4.54) является нормированной корреляционной зависимостью и показывает степень корреляции между ошибкой прямого предсказания и ошибкой обратного предсказания. Поэтому коэффициенты km иногда называют коэффициентами частной корреляции. Уравнение (4.54) может использоваться вместо уравнения (4.36) при оценивании коэффициентов линейного предсказания.

Оценки коэффициентов km лестничного фильтра, вычисленные с помощью (4.54), будут находиться в диапазоне —1<Ат^1. Достоинством лестничного фильтра является низкая чувствительность к шумам округления. Соответственно коэффициенты лестничного фильтра допускают более грубое квантование. Благодаря этому гарантируется получение устойчивого фильтра.

Важное отличие оценивания ЛПК с использованием лестничного фильтра от автокорреляционного подхода состоит в том, что коэффициенты km оцениваются непосредственно по речевому сигналу без вычисления автокорреляционной функции.

Обратим внимание на то, что лестничный фильтр, изображенный на рис.4.12, в соответствии с (4.45) имеет передаточную функцию A(z). При этом A(z) является обратной по отношению к передаточной функции предсказывающего фильтра (4.25). Поэтому, при подаче на вход лестничного фильтра речевого сигнала s[n\, на выходе формируется сигнал и[п\, т.е. функция возбуждения. Иными словами, ошибка предсказания d\n\ соответствует функции возбуждения.