4.5 Гомоморфная обработка речи
В соответствии с рис.4.1 речевой сигнал является сверткой функции возбуждения (случайного шума либо квазипериодической последовательности импульсов) и импульсной характеристики голосового тракта. Гомоморфный анализ речи позволяет разделить эти компоненты. Поэтому, используя гомоморфный анализ, можно определить период основного тона и частотные свойства голосового тракта. Общая схема гомоморфной обработки приведена на рис.4.7.
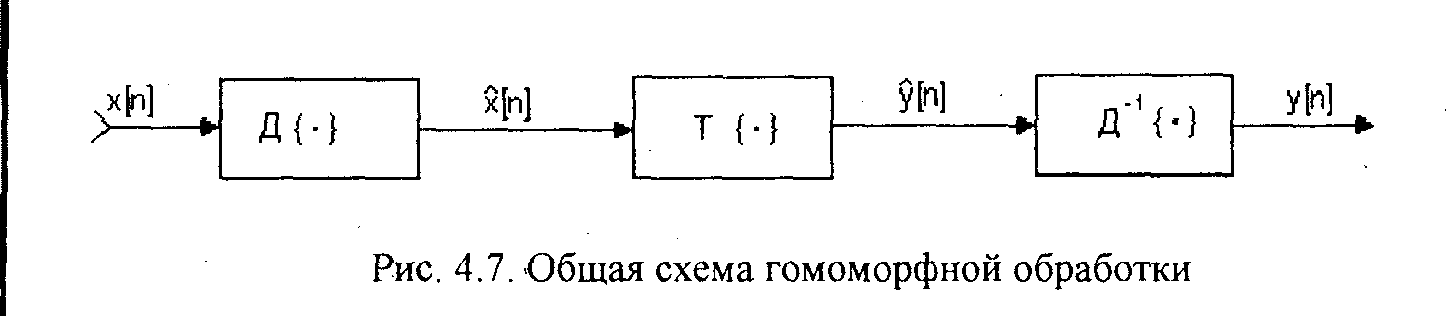
В соответствии с этой схемой сначала выполняется нелинейное преобразование Д{ } сигналах, которое определяется соотношением
X(z}=X^z)-Xi(z). (4.16)
Подставив (4.16) в (4.15), получим
Линейная инвариантная система пропускает на выход только одну из компонент X\(z) или X:(z). Соответственно обратное преобразование Д"'{ } дает ^["]=-ci[/!] или ^[и]=-Т2[я]. Следовательно, гомоморфная обработка разделяет входные компоненты х\[п} и хг[п], содержащиеся во входном сигнале.
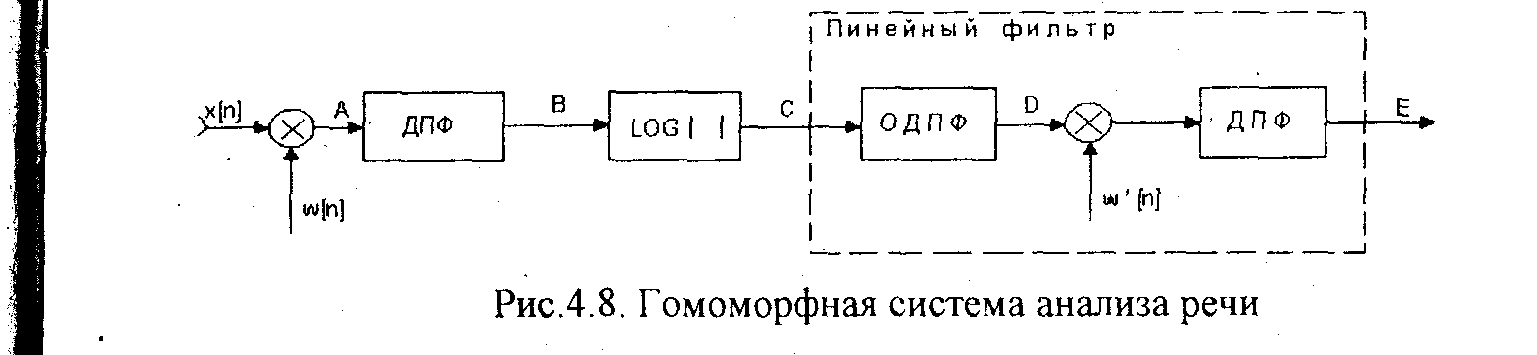
Гомоморфная система анализа речи показана на рис.4.8. Здесь на первом этапе вычисляется логарифм модуля кратковременного преобразования Фурье. Если предположить, что сигнал в точке А является сверткой функции возбуждения и импульсной характеристики голосового тракта, то в точке С мы получим сумму логарифмов спектра функций возбуждения и импульсной характеристики голосового тракта. Сигнал в точке D, полученный с помощью обратного дискретного преобразования Фурье, называется кепстром. Кепстр в точке D равен сумме кепстров функции возбуждения и импульсной характеристики голосового тракта. Покажем это.
В общем случае, комплексный кепстр сигнала х[п] определяется как обратное преобразование Фурье от логарифма комплексного спектра Х(ш).
Для модуля кратковременного спектра |^('У)|, который является четной и периодической функцией, можно использовать разложение в ряд Фурье
где с[п] - кепстральные коэффициенты и
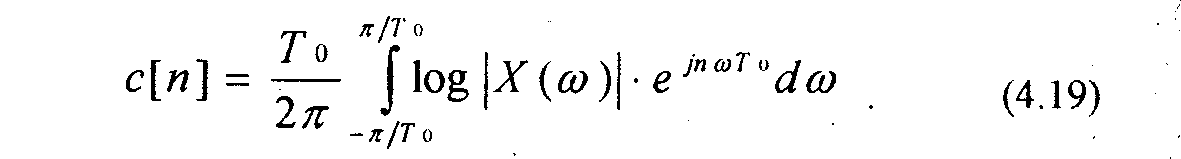
Если речевой сигнал является сверткой функции возбуждения и[п] и импульсной характеристики h[n] голосового тракта
то модуль спектра |^(<у)| равен произведению модулей \U(a)}\ и \Н(а>)\:
Взяв логарифм от обеих частей (4.21), получим
Так как обратное преобразование Фурье является линейной операцией, то из(4.22) следует, что
где с„[и) и Сн[п] - кепстры последовательностей и[п\ и h[n].
В схеме обработке речи, изображенной на рис.4.8 , вместо дискретно-непрерывного преобразования Фурье по непрерывной перемененной q) используется дискретное преобразование Фурье, определяемое на фиксированных частотах. Рис.4.9 иллюстрирует указанные преобразования для вокализованной речи.
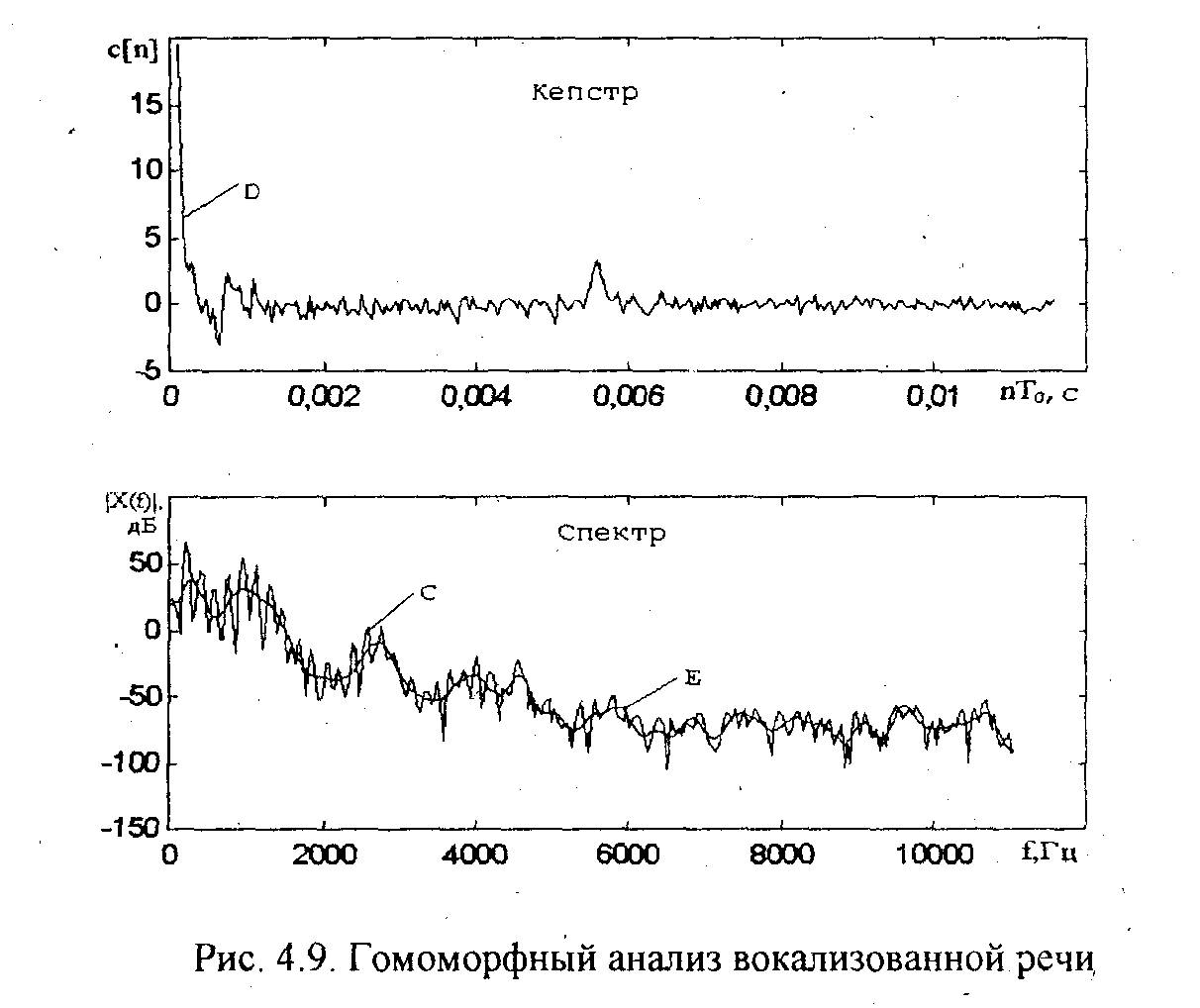
Пульсирующая кривая С (рис.4.9) соответствует логарифму модуля кратковременного спектра. Она содержит медленно меняющуюся составляющую, соответствующую амплитудно-частотной характеристике голосового тракта, и быстро меняющуюся составляющую, обусловленную периодической функцией возбуждения. Выполнив ОДПФ логарифма спектра, получим кепстр, который является функцией времени. Медленно меняющаяся составляющая спектра соответствует области малых времен кепстра, а быстро меняющаяся периодическая составляющая спектра соответствует удаленному пику в кепстре (рис.4.9), возникающему через интервал времени, равный периоду основного тона. Для невокализованной речи указанный пик будет отсутствовать. Поэтому кепстр может использоваться для определения периода основного тона и характера речи (вокализованная или невокализованная).
Амплитудно-частотная характеристика голосового тракта получается низкочастотной фильтрацией сигнала, действующего в точке С (рис.4.8). В результате этого будут подавлены быстро меняющиеся элементы на кривой С (рис. 4.9). Фильтрация может быть выполнена по методу быстрой свертки. Для этого вычисляется ОДПФ сигнала С, полученный кепстр умножается на подходящую функцию окна, пропускающую лишь область ;i малых времен кепстра, и затем выполняется ДПФ. В результате такой обработки получим сглаженный спектр (рис. 4.9, кривая Е). Резонансные пики на кривой Е позволяют определить формантные частоты. Используя оценки формантных частот голосового тракта и период основного тона, можно синтезировать речь на основе модели, изображенной на рис.4.1.