Алгоритмы растровой графики: алгоритмы заливки замкнутых фигур с границей заданного цвета, заливка многоугольников.
Подавляющее число графических устройств являются растровыми, представляя изображение в виде прямоугольной матрицы (сетки, целочисленной решетки) пикселов (растра), и большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов, таких, как:
переведение идеального объекта (отрезка, окружности и др.) в их растровые образы;
обработка растровых изображений.
Тем не менее часто возникает необходимость и явного построения растровых алгоритмов.
Достаточно важным понятием для растровой сетки является связность - возможность соединения двух пикселов растровой линией, т. e. последовательным набором пикселов. Возникает вопрос, когда пикселы (x1,y1) и (х2,у2) можно считать соседними.
Вводится два понятия связности:
• 4-связность: пикселы считаются соседними, если либо их x-координаты, либо их у-координаты отличаются на единицу:
• 8-связность: пикселы считаются соседними, если их x-координаты и y-координаты отличаются не более чем на единицу:
Понятие 4-связности является более сильным: любые два 4-связных пиксела являются и 8-связными, но не наоборот. На рис. 6.1 изображены 8-связная линия (а) и 4-связная линия (б).
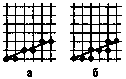
Puc.6.1
В качестве линии на растровой сетке выступает набор пикселов P1, P2,..., Рn, где любые два пиксела Pi, Pi+1 являются соседними в смысле заданной связности.
Алгоритм закраски многоугольников.
Под многоугольником далее будем понимать фигуру, ограниченную на плоскости простой (непересекающейся) замкнутой ломаной. Сама ломаная задается координатами вершин Ai(xi,yi), i=1..n, при этом соседние точки в этом списке являются вершинами ломаной. Задача "закраски" многоугольника заключается в инициализации все его внутренние точки. Наиболее простой, но и наиболее медленный алгоритм, решающий эту задачу состоит в том, чтобы проверить все точки плоскости (под плоскостью здесь естественно понимается устройство, на которое осуществляется вывод, в нашем случае это массив Screen) на принадлежность многоугольнику. Несколько ускорить этот алгоритм можно, если вместо проверки всех точек плоскости проверять только точки минимального квадрата заключающего многоугольник, найти который, не составляет труда. Ясно, что и при таком усовершенствовании скорость работы алгоритма оставляет желать лучшего.
Еще один вариант решения задачи, это алгоритм сканирования строк. Последовательно проходим все горизонтальные линии плоскости, и находим отрезки на прямой, внутренние для многоугольника. Для данного алгоритма достаточно искать только точки пересечения сканирующей линии с ребрами многоугольника. Для оптимизации алгоритма можно упорядочить ребра в порядке возрастания наибольшей из ординат концов. При перемещении сканирующей прямой сверху вниз проверке на пересечение подвергаются лишь те ребра, у которых значение максимальной ординаты больше ординаты сканирующей прямой. Такой алгоритм пригоден для заполнения произвольных многоугольников. Но если многоугольник выпуклый, то алгоритм можно упростить и существенно повысить его эффективность. Для этого заметим, что границу выпуклого многоугольника можно разбить на две ломаные "левую" и "правую" и, возможно, два ребра "верхнее" и "нижнее" так что каждая из боковых ломаных имеет ровно одно пересечение с каждой сканирующей прямой. Далее, используя алгоритм Брезенхейма и одновременно генерируя растровое представление для ребер левой и правой части ломаных границ, получаем левый и правый пиксели границы многоугольника на каждой сканирующей горизонтальной прямой. Последовательно заполняя интервалы между этими пикселами для каждого значения ординаты от верхней строки развертки до нижней, получим растровое представление многоугольника.
Алгоритм закраски произвольной области с затравкой.
Рассмотрим еще один класс алгоритмов "закраски", а именно алгоритмы заполнения области с затравкой. В этих алгоритмах предполагается, что граница области задана на растровой плоскости и указана одна из внутренних точек области, которая называется затравочной. Требуется заполнить определенным цветом связную компоненту области, содержащую затравочную точку. Под связностью будем понимать 4-х или 8-ми связности, определенные выше (какая связность конкретно используется, зависит от формулировки задачи). Данному классу алгоритмов можно сопоставить физическую интерпретацию, а именно представить, что в затравочной точке помещен источник, заливающий всю область определенным цветом. Поэтому часто такие алгоритмы называют алгоритмами заливки. В связи с той физической интерпретацией, которую мы имеем, можно получить очевидный алгоритм решающий задачу заливки области. Допустим нам надо "закрасить" цветом IColor область, граница, которой имеет цвет BColor, и нам задана точка с координатами (x0,y0) в качестве затравочной.
Поместим затравочную точку на стек.
Извлекаем координаты точки с вершины стека в переменные (x,y)
Если Screen[x,y]=IColor, то Screen[x,y]=IColor
Для всех соседних точек (xg,yg) повторить пункт 5
Если Screen[xg,yg]<>BColor и Screen[xg,yg]<>IColor, то поместить точку (xg,yg) на стек.
Если стек не пуст, то переходим к пункту 3.
Соседние точки, пункта 4 алгоритма, определяются в зависимости от того, какое условие связности определенно в условие задачи. Приведенный алгоритм весьма неэффективен, так как предполагает неоднократную обработку одних и тех же точек и неконтролируемый рост размера стека. Поэтому усовершенствуем его, используя идею, примененную нами в алгоритме построчного сканирования. Заметим, что на каждой строке множество точек подлежащих закраске, состоит из интервалов, принадлежащих внутренности области. Эти интервалы отделены друг от друга интервалами из точек, принадлежащих границе или внешности области. Кроме того, если набор точек образует связный интервал, принадлежащий внутренней части области, то точки над и под этим интервалом либо являются граничными, либо принадлежат внутренней части области. Последние могут служить затравочными для строк лежащих выше и ниже рассматриваемой строки. Суммируя все это, можно предложить следующий алгоритм.
Поместим затравочную точку на стек.
Извлекаем координаты точки с вершины стека в переменные (x,y)
Заполняем максимально возможный интервал, в котором находится точка, вправо и влево вплоть до достижения граничных точек.
Запоминаем крайнюю левую xl и крайнюю правую xr абсциссы заполненного интервала.
В соседних строках над и под интервалом (xl,xr) находим незаполненные к настоящему моменту внутренние точки области, которые объединены в интервалы, а в правый конец каждого такого интервала помещаем на стек.
Если стек не пуст, то переходим к пункту 3.