
- •Лабораторная работа № 1 Расчет цифровых фильтров в пакете MatLab с учетом квантования
- •1. Цель работы
- •2. Проектирование цифровых фильтров с помощью пакета Filter Desing
- •3. Домашнее задание
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •6. Исходные данные для выполнения лабораторной работы
- •Лабораторная работа № 2 Дискретное преобразование Фурье (дпф)
- •1. Цель работы
- •2. Основные положения дпф
- •3. Домашнее задание
- •4. Порядок выполнения работы
- •5. Содержание отчета
- •6. Контрольные вопросы
- •7. Исходные данные для выполнения лабораторной работы
- •Лабораторная работа № 3 Исследование аналого-цифрового преобразователя (ацп)
- •1. Цель работы
- •2. Описание работы ацп в пакете Simulink
- •3. Настройка параметров модели
- •4. Домашнее задание для выполнения лабораторной работы
- •5. Порядок выполнения лабораторной работы
- •6. Содержание отчета
- •7. Контрольные вопросы
- •8. Исходные данные для выполнения лабораторной работы
Лабораторная работа № 2 Дискретное преобразование Фурье (дпф)
1. Цель работы
1. Изучить процессы и особенности применения ДПФ к дискретным последовательностям.
2. Изучить свойство ДПФ.
3. Изучить команды MatLab, осуществляющие прямое и обратное ДПФ.
4. Изучить частотные характеристики ДПФ и свойство ДПФ проявляющиеся при анализе произвольных последовательностях.
2. Основные положения дпф
Информация о
процессах и сигналах может передаваться
функциями времени
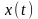 или частотным спектром
или частотным спектром
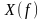 .
Связь между
и
определяется преобразованием Фурье
.
Связь между
и
определяется преобразованием Фурье
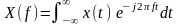 (1)
(1)
где – некоторый непрерывный сигнал во временной области.
Выражение (1) позволяет определить частотный состав практически любого сигнала , используемого на практике, и открывает широкие возможности для анализа и обработки сигналов в физике и технике.
С появлением
цифровой техники, широкое распространение
получило дискретное преобразование
Фурье (ДПФ), позволяющее определять
дискретную последовательность
 (дискретный спектр) в частотной области.
(дискретный спектр) в частотной области.
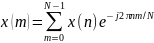
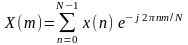 . (2)
. (2)
Существует и обратное преобразование Фурье. Переход от дискретного спектра к временным отсчетам выражается следующей формулой:
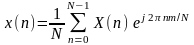 . (3)
. (3)
Выражение (3)
определяет обратное дискретное
преобразование Фурье (ОДПФ) и отличается
от выражения (2) (ДПФ) лишь знаком в
показателе комплексной экспоненты и
наличием множителя
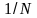 .
В размещении множителя
нет полного единства. В большинстве
источников (в том числе и в пакете MatLab)
множителя фигурирует в формуле ОДПФ. В
тоже время имеются работы, в которых
этот множитель стоит в формуле прямого
ДПФ. Существуют пакеты программ, в
которых используется множитель
.
В размещении множителя
нет полного единства. В большинстве
источников (в том числе и в пакете MatLab)
множителя фигурирует в формуле ОДПФ. В
тоже время имеются работы, в которых
этот множитель стоит в формуле прямого
ДПФ. Существуют пакеты программ, в
которых используется множитель
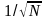 ,
который стоит перед определениями
суммирования в форме прямого и обратного
ДПФ.
,
который стоит перед определениями
суммирования в форме прямого и обратного
ДПФ.
Уравнение (2) – это основная запись ДПФ в технической литературе. Однако для реализации ДПФ, особенно на начальном этапе, целесообразно перейти к тригонометрической форме ДПФ
 (4)
(4)
Переход от (2) к (4) осуществлен на основании тождества Эйлера
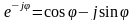
Выражения (4) позволяет комплексную экспоненту в (2) представить в виде действительной и мнимой части, где:
–
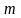 -й
компонент ДПФ, т.е.
-й
компонент ДПФ, т.е.
 ,
,
 ,
,
 и т.д.
и т.д.
– индекс ДПФ в частотной области, =0,1,2,3,4…., N-1.
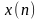 -
последовательность входных отсчетов
-
последовательность входных отсчетов
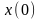 ,
,
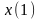 ,
,
 ,
,
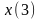 и т.д.
и т.д.
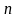 - временной индекс
входных отсчетов,
=0,1,2,3,…,
- временной индекс
входных отсчетов,
=0,1,2,3,…,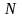 -1.
-1.
–определяет и
количество отсчетов входной
последовательности, и количество
частотных отсчетов результата ДПФ
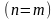 .
.
Рассмотрим выражение (4), записав слагаемые суммы по отдельности. Для иллюстрации возьмем малое число отсчетов. Например, при =4 и , и принимают значение от 0 до 3, а выражение (4) превращается, в зависимости от исходных данных, в развернутое выражение
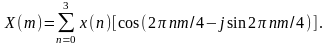 (5)
(5)
Из (5) следует, что
для определения первого отсчета ДПФ
(
=?)
необходимо: подставить в (5) соответствующие
значения индекса
(
=0)
и получить четыре слагаемые в функции
(
=0,1,2,3)
путем умножения временных последовательностей
на гармонические функции
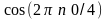 и
и
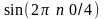 ,
изменяющиеся в функции
.
Причем, первый отсчет ДПФ определяет
постоянную составляющую временной
последовательности
.
,
изменяющиеся в функции
.
Причем, первый отсчет ДПФ определяет
постоянную составляющую временной
последовательности
.
Для определения второго отсчета ДПФ (первой гармоники) ( =1) необходимо:
- подставить в (5) соответствующие значения индекса , т.е. =1;
- получить четыре
слагаемые в функции
(
=4)
путем умножения временной последовательности
на первые гармоники
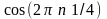 и
и
 ,
дискретные значения которых определяются
параметром
.
,
дискретные значения которых определяются
параметром
.
Таким образом,
каждый отсчет ДПФ
,
определенный по формуле (2) или (4),
представляет собой сумму почленных
произведений входной последовательности
отсчетов сигнала
на последовательность отсчетов дискретных
гармонических функций
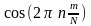 и
и
 .
Сравнение формул для определения
коэффициентов ряда
.
Сравнение формул для определения
коэффициентов ряда
 и
и
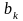 ,
используемых для представления в ряд
непрерывных функций
,
используемых для представления в ряд
непрерывных функций
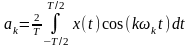 ,
,  ,
,
с
выражением (5) показывает, что соответствующие
значения
ДПФ являются аналогом коэффициентов и
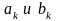 .
.
В технике большое распространение находит комплексная форма представления рядов Фурье, которые можно получить из косинусно-синусной формы путем использования тождества Эйлера

Таким образом, ДПФ применяется в двух формах. Расчеты с использованием выражения (2) определяют гармоники в показательной форме, а с использованием выражение (4) - в алгебраической форме. Связь между двумя представлениями комплексных чисел связана известными соотношениями:
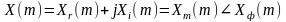
где
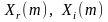 - проекции
- проекции
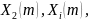 модуля
на действительную и мнимую ось,
соответственно;
модуля
на действительную и мнимую ось,
соответственно;
 -
-
 модуль
комплексного числа;
модуль
комплексного числа;
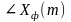 - угол между модулем и действительной
осью.
- угол между модулем и действительной
осью.
Довольно часто нас интересует как амплитуда так и мощность (амплитуда в квадрате) каждого отсчета (каждой гармоники). Для их вычисления применимы стандартные соотношения прямоугольного треугольника
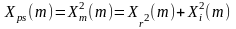 ,
,
где
 -мощность
отсчетов
,
которая называется спектром мощности
и представляет собой амплитуду,
возведенную в квадрат.
-мощность
отсчетов
,
которая называется спектром мощности
и представляет собой амплитуду,
возведенную в квадрат.
В результате ДПФ
определяют зависимость модуля или его
составляющих (действительной и мнимой
части) как функцию
(количества отсчетов, количество бинов).
В тоже время желательно представить
расчеты как функцию частоты в Герцах
( ),
которая зависит от частоты дискретизации
),
которая зависит от частоты дискретизации
 ,количества
отсчетов
,
и натурального ряда чисел
(
-номера
бина, отсчета, гармоники)
,количества
отсчетов
,
и натурального ряда чисел
(
-номера
бина, отсчета, гармоники)
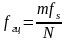 .
.
Не зная частоты дискретизации мы не можем сказать с каким временным интервалом брались отсчеты, следовательно, не знаем масштаб частотной оси. Например, при =500 отсчетов в секунду и при =16 (16-точечные ДПФ) основная гармоника (основная частота) будет равна
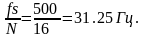
Другие частоты
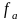 ,
кратные основной, будут определяться
выражением
,
кратные основной, будут определяться
выражением
 . (6)
. (6)
Если увеличится в два раза то, при неизменном количестве отсчетов ( =16), изменится масштаб и, соответственно, в два раза будут увеличены циклические частоты, в функции которых анализируемого графики исследуемых сигналов. Используя (6) можно записать:
-1-й частотный отсчет (постоянная составляющая равна 0*31.25=0 Гц)
-2-й частотный отсчет (первой гармоники равной 1*31.25=31,25 Гц)
Аналогично получаем остальные отсчеты (гармоники, бины) вплоть до 4 четвертого отсчета (третьей гармоники).
Таким образом, при =4 и при =500 ДПФ сообщает нам следующие данные: значение постоянной составляющей; амплитуды составляющих сигналов с частотами 31.25 Гц, 62.5 Гц и 93.75 Гц.
Для изучения
свойств ДПФ рассмотрим следующий пример.
Задан непрерывный двухчастотный сигнал
(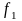 =1000 Гц
и
=1000 Гц
и
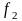 =2000 Гц)
=2000 Гц)
 , (7)
, (7)
над
которым осуществлено 8-точечные ДПФ.
Чтобы сделать анализ более информативным,
составляющая
сдвинута по фазе на
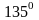 (3π/4) по отношению к частоте
.
Выбираем частоту дискретизации
=8000
Гц и осуществим частотный анализ
выходного сигнала (7). При заданный
и
ДПФ будет определять проекции амплитуд
составляющих спектра, содержащаяся в
на частотных
или 0,1кГц, 2кГц, …, 7кГц. Расчеты выполнены
по выражению (7) и представлены в
алгебраической и показательной формах
(3π/4) по отношению к частоте
.
Выбираем частоту дискретизации
=8000
Гц и осуществим частотный анализ
выходного сигнала (7). При заданный
и
ДПФ будет определять проекции амплитуд
составляющих спектра, содержащаяся в
на частотных
или 0,1кГц, 2кГц, …, 7кГц. Расчеты выполнены
по выражению (7) и представлены в
алгебраической и показательной формах
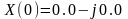
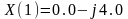 =
4
=
4
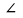 -
-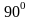
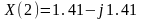 =2
=2


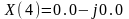
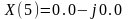
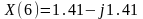 =2
-
=2
-
 =
4
=
4
Используя
вышеприведенные данные, построены
четыре графика: зависимость модуля
,
фазы
 ,
действительной части
,
действительной части
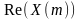 и мнимой части
и мнимой части
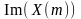 от
частоты.
от
частоты.
Из рис.1 следует,
что комплексные отсчеты ДПФ для
от 1 до (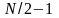 )
тесно связаны с частотными отсчетами
гармоник с
>
)
тесно связаны с частотными отсчетами
гармоник с
>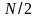 ,
-й
отчет ДПФ имеет тот же модуль, что и
,
-й
отчет ДПФ имеет тот же модуль, что и
 -
й отчет. Фазовый угол
-
го отсчета ДПФ равен фазовому углу
- го отсчета, взятому с противоположным
знаком. Таким образом,
-
й и
-
й отсчеты связаны следующим соотношениями:
-
й отчет. Фазовый угол
-
го отсчета ДПФ равен фазовому углу
- го отсчета, взятому с противоположным
знаком. Таким образом,
-
й и
-
й отсчеты связаны следующим соотношениями:
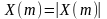 с
углом
гр.
=
с
углом
гр.
=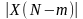 с углом
с углом
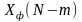 гр. (8)
гр. (8)
На основании (8)
можно утверждать, что для действительной
входной последовательности
,
отсчеты
образуют с отсчетами
 комплексно-сопряженную пару
комплексно-сопряженную пару
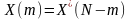 ,
,

Рис.1. Результаты расчетов: 1-амплитудный спектр ); 2-фазовый спектр ; 3- действительная часть ; 4- мнимая часть
где, верхний индекс * обозначает комплексную сопряженность.
ДПФ позволяет
определить N комплексных отсчетов, но
только
 из этих отсчетов будут независимыми.
Остальные отсчеты могут быть вычислены
по уравнению (8) на основании свойств
симметрии, т.е. отсчеты от
из этих отсчетов будут независимыми.
Остальные отсчеты могут быть вычислены
по уравнению (8) на основании свойств
симметрии, т.е. отсчеты от
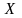 (
)
до
(
)
до
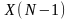 не дают дополнительной информации.
не дают дополнительной информации.
В результате применения ДПФ к выражению (7) определили частоты и амплитуды исходного сигнала. Причем, если частоты, полученные в результате анализа, совпали с частотами входного сигнала, то амплитуды сигналов, определенных ДПФ, увеличены в 4 раза, т.е. изменился масштаб амплитуд. Причем, если бы к выражению (7) было применено 16-точечное преобразование Фурье, то амплитуда спектральных составляющих были бы увеличены в 8 раз.
Таким образом,
чтобы амплитуды, полученные в результате
ДПФ, совпадали с амплитудами исходного
сигнала, результаты расчетов должны
корректироваться, т.е. умножиться на
коэффициент, пропорциональный

В результате применения ДПФ определится комплексный спектр в дискретных точках, заданных параметром . Например, если =8, то спектр определяется в 8 точках; если =16, то спектр-в 16 точках. Для перехода от параметра , который определяет номер гармоники и изменяется от 0 до N-1, к частоте в Гц. необходимо знать частоту дискретизации . Связь между частотой в Гц. и гармониками определяется соотношением (9).
 . (9)
. (9)
Таким образом, одному и тому же графику, построенному в результате применения 8-точечного ДПФ, могут соответствовать разные частотные оси, выраженные в Гц. Например, если равна 8000 отсчетов в секунду, то первая гармоника соответствует частоте 1000 Гц
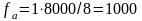 Гц.
Гц.
Если же выполнить то же ДПФ, но частоту дискретизации уменьшить в 10 раз, то первой гармонике будет соответствовать частота 100 Гц.
Итак, в результате применения ДПФ узнали:
- каждый выходной отсчет ДПФ есть сумма почленных произведений входной последовательности на последовательности, представляющий синусоидальный и косинусоидальные сигналы;
- значение определяет количество входных отсчетов, разрешающую способность по частоте и время, необходимое для вычисления – точеного ДПФ;
- для действительных сигналов – точеное ДПФ дает только независимых отсчетов;
- ДПФ представляет собой линейную операцию;
- модули результатов ДПФ прямо пропорциональны ;
- разрешающая
способность ДПФ по частоте составляет
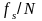 .
.
При увеличении обьем расчетов по определению спектральных составляющих возрастает. Поэтому целесообразно использовать пакет MatLab, в котором для выполнения прямого и обратного ДПФ используются функции fft и ifft:
y= fft(x) – вычисляет прямое ДПФ для вектора ; если -матрица, то преобразование производится для каждого столбца в отдельности .
y= fft(x, N) – предварительно приводит данные к размеру , урезая их или дополняя нулями. Размер обычно задается как 2 в некоторой степени.
x= ifft(y) и x=ifft(y, N) - аналогичные команды для вызова функции обратного ДПФ.
В результате применения функции fft получим комплексную составляющую спектра исходного сигнала, представленную в алгебраической форме. По составляющим вектора можно определить модуль, отдельно действительную и отдельно мнимую составляющие спектра (Программа 1). При построении графиков в качестве независимой переменной используется (номер отсчета). Графики частотной области для дискретных сигналов удобнее выводить при помощи процедуры stem.
Программа 1 (fur_l_01.m)
N=8; %Количество отсчетов.
n=0:1:7; %Индексы отсчетов.
t=1/8000; %Частота дискретизации.
x=sin(2*pi*1000*n*t)+0.5*sin(2*pi*2000*n*t+3*pi/4);%Входной сигнал.
figure(1)
plot(x),grid on %График анализируемого сигнала.
y=fft(x) %Преобразование Фурье.
figure(2) %График действительной составляющей.
stem(real(y)),grid on
figure(3)
stem(imag(y)),grid on %График мнимой составляющей.
Xm=abs(y)
figure(4) %График модуля гармоник.
stem(Xm),grid on
Xmm=2*abs(y)/N
figure(5)
stem(Xmm),grid on %График модуля гармоник (нормированный).
1
2
3
4
5
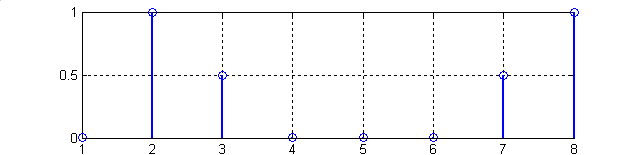
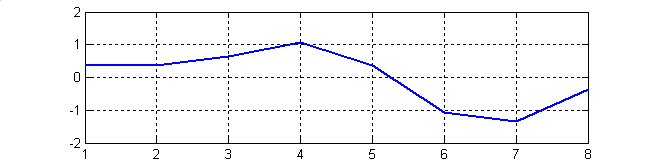
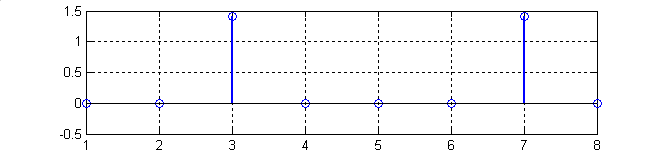
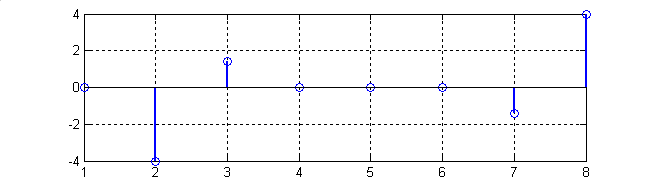
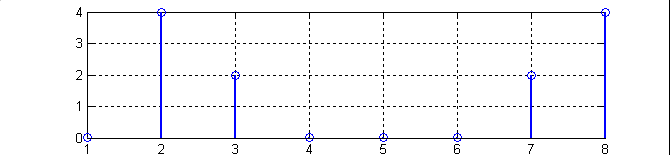
Рис.2. Графики, иллюстрирующие Программу 1: (1-исходная последовательность; 2-действительная часть ДПФ; 3-мнимая часть ДПФ; 4- модуль ДПФ не нормированный; 5-модуль ДПФ нормированный.)
Графики в Программе
1 дают избыточную информацию, так как
построены для всех значений
,
и не очень удобны для интерпретации.
Более привычным является график, в
котором входная последовательность
начинается при отрицательных значениях
,
а нулевая точка является средней точкой
дискретной последовательности. В этом
случае спектральные характеристики
представляются графиком, имеющим
отрицательные и положительные отсчеты,
а нулевой отсчет расположен в центре и
соответствует постоянной составляющей
(Программа 2).Для преобразования графиков
с нулевым отсчетом, расположенным в
центре, используется функция fftshift,
которая помещает нулевую частоту в
центре графика, а диапазон отображаемых
частот простирается от -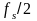 до
.
до
.
Программа 2 (fur_L_02.m)
N=8; %Количество отсчетов.
n=0:1:7; %Индексы отсчетов.
t=1/8000; %Частота дискретизации.
x=sin(2*pi*1000*n*t)+0.5*sin(2*pi*2000*n*t+3*pi/4); %Входной сигнал.
figure(1)
stem(x),grid on %Дискретные отсчеты входного сигнала.
y=fft(x); %Преобразование Фурье.
Xm=abs(y)/4 %Модуль преобразования Фурье.
figure(2)
stem(Xm),grid on %График нормированного модуля.
xp=fftshift(y) %Преобразование Фурье с использованим
%отрицательных частот.
f=-N/2:1:(N/2-1) %Диапазон частот команды xp=fftshift(y).
a=abs(xp)/4 %Модуль преобразования Фурье в новой системе
%координат.
figure(3) %График нормированного модуля с использованим
stem(f,a),grid on %отрицательных частот
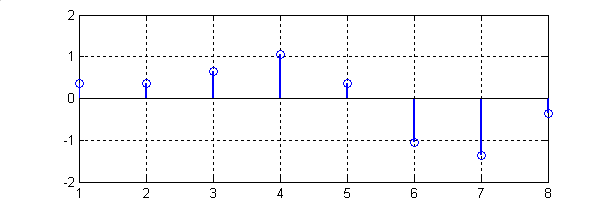
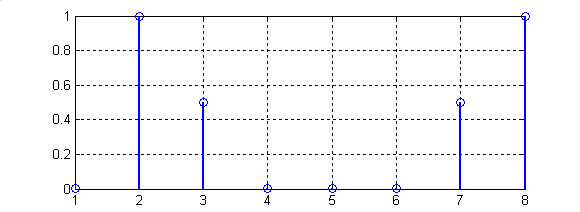
Результаты выполнения "Программы 2" представлены на рис.3
1
2
3
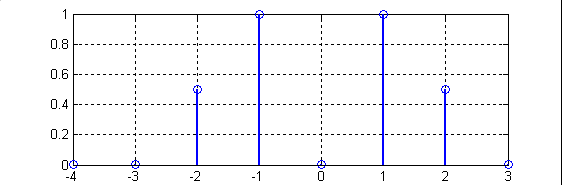
Рис.3.
Графики, иллюстрирующие Программу 2:
(1-исходная последовательность;
2-нормированное ДПФ в функции частот от
0 до
 ;
3-нормированное ДПФ в функции частот от
;
3-нормированное ДПФ в функции частот от
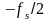 до
)
до
)
Результаты расчетов (выполненя Программ) показали идеальный результат: входной сигнал имел две частоты =1000 Гц и =2000 Гц с амплитудами, соответственно, 1 и 0.5. Эти же значения в точности были получены в результате расчетов. Однако ДПФ дает правильный результат только тогда, когда входная последовательность содержит энергию точно на аналитической частоте ( -частота, кратная фундаментальной частоте ).
 , (10)
, (10)
= 0,1,2,…, .
Если входной сигнал
содержит компонент с некоторой
промежуточной частотой, лежащий между
аналитическими частотами
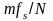 ,
скажем
,
скажем
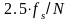 ,
то этот входной сигнал проявится в
некоторой степени на всех
частотах, на всех выходных бинах (часто
отсчеты для построения графиков ДПФ
называют бинами).
,
то этот входной сигнал проявится в
некоторой степени на всех
частотах, на всех выходных бинах (часто
отсчеты для построения графиков ДПФ
называют бинами).
Программа 3 (fur_L_0.3.m).
N=8; %Количество отсчетов.
n=0:1:7; %Индексы отсчетов.
t=1/8000; %Частота дискретизации.
x=sin(2*pi*2200*n*t); %Анализируемый сигнал.
y=fft(x); %Преобразование Фурье в диапазоне 0-(N-1).
xp=fftshift(y) %Преобразование Фурье в диапазоне (–N/2)-(N/2-1).
f=-N/2:1:(N/2-1)
a=abs(xp)/4 %Нормированный модуль в диапазоне (–N/2)-(N/2-1).
figure(1) %График нормированного модуля
stem(f,a),grid on %в диапазоне (–N/2)-(N/2-1).
x2=sin(2*pi*2500*n*t); %Анализируемый сигнал.
y2=fft(x2); %Преобразование Фурье в диапазоне 0-(N-1).
xp2=fftshift(y2) %Преобразование Фурье в диапазоне (–N/2)-(N/2-1).
a2=abs(xp2)/4 %Преобразование Фурье в диапазоне (–N/2)-(N/2-1).
figure(2) %График нормированного модуля
stem(f,a2),grid on %в диапазоне (–N/2)-(N/2-1).
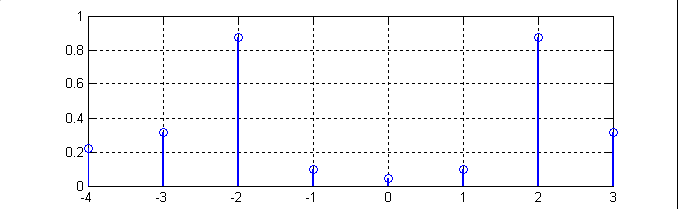
По результатам выполнения Программы 3 представлено два рисунка, иллюстрирующие спектральный состав двух входных последовательностей.
1
2
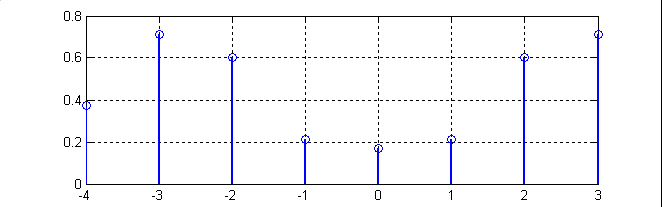
Рис.4. Графики, иллюстрирующие Программу 3: (1-спектральные составляющие входной последовательности с частотой 2200 Гц; 2-спектральные составляющие входной последовательности с частотой 2500 Гц.)
Из рисунка 4
следует, что несущественно изменив
входные последовательности мы существенно
изменили спектр: появились спектральные
составляющие на всех отсчетах, в том
числе и постоянная составляющая при
=0.
Рис.4.2 отличается от рис.4.1 тем, что
анализируемая последовательность ( дальше отстоит от аналитических частот
(
дальше отстоит от аналитических частот
(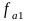 =2000Гц
и
=2000Гц
и
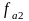 =3000Гц).
Это приводит к большему искажению
спектра: увеличилась амплитуда постоянной
составляющей, и увеличились амплитуды
всех гармоник, кроме одной (
=2),
которая уменьшается.
=3000Гц).
Это приводит к большему искажению
спектра: увеличилась амплитуда постоянной
составляющей, и увеличились амплитуды
всех гармоник, кроме одной (
=2),
которая уменьшается.
Таким образом, с удалением частоты исходной последовательности от частот, определяемых выражением (10), разрешающая способность ДПФ падает, а амплитуда входного сигнала проявляется во всех бинах. Этот эффект наблюдаться для всех входных последовательностей, которые не имеют целого числа периодов на интервале отсчета ДПФ. В этом случае энергия входного сигнала «протекает» во все отчеты (во все гармоники), во все бины ДПФ.
Закон, по которому распределяется утечка, зависит от количества точек исходной последовательности , индекса бина и аппросимируется функцией sinc
 . (11)
. (11)
В программе 4 представлена решетчатая функция, построенная по выражению (11), для разных значений интервалов дискретности (рис.5.1 и рис.5.2).
Программа 4 (fur_l_0.4.m).
N=8; %Количество отсчетов.
n=0:1:7; %Индексы отсчетов.
t=1/8000; %Частота дискретизации.
x=sin(2*pi*2200*n*t); %Анализируемый сигнал.
y=fft(x); %Преобразование Фурье в диапазоне 0-(N-1).
xp=fftshift(y) %Преобразование Фурье в диапазоне (–N/2)-(N/2-1).
f=-N/2:1:(N/2-1)
a=abs(xp)/4 %Нормированный модуль в диапазоне (–N/2)-(N/2-1).
figure(1) %График нормированного модуля
stem(f,a),grid on %в диапазоне (–N/2)-(N/2-1).
N=8; %Количество отсчетов.
n=0:7; %Индексы отсчетов.
y=sinc(n) %Функция, определяющая размывание спектра для идекса n.
t=0:0.25:7; %Индексы отсчетов увеличенной размерности.
y1=sinc(t) %Функция, определяющая размывание спектра для идекса t.
figure(1) %График функции y=sinc(n).
stem(n,y),grid on
figure(2) %График функции y1=sinc(t).
stem(t,y1),grid on
1
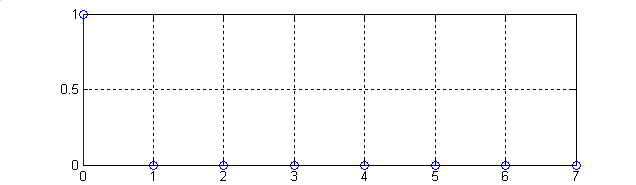
2
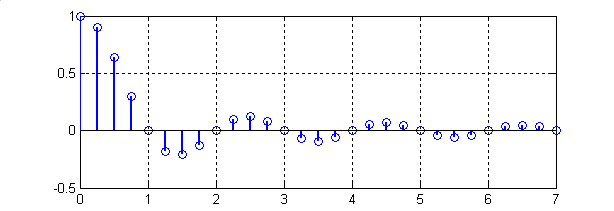
Рис.5. Амплитудно-частотная
характеристика выражения(11) как функции
бина (1-число бинов совпадает с количеством
отсчетов входной последовательности
(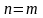 );
2-число n отсчетов входной последовательности
больше числа бинов (
);
2-число n отсчетов входной последовательности
больше числа бинов (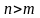 )).
)).
Из рис.5 следует,
что амплитудно-частотная характеристика
функции sinc состоит из главного лепестка
и периодически повторяющихся пиков и
впадин, которые называются боковыми
лепестками. Результатом дискретизации
функции sinc (результататом применения
ДПФ) являются дискретные отсчеты, которые
лежат на непрерывной кривой sinc, т.е.
результат ДПФ представляет собой
дискретизированную аппроксимацию
непрерывного спектра (рис.5.2). На рис.5.1
представлен такой вариант дискретизации
спектра, когда
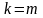 и все бины, кроме центрального бина,
характеризуются нулевым спектром. Если
входная последовательность ДПФ имеет
ровно k полных периодов (т.е. центральная
частота ее спектра точно совпадает с
бином
и все бины, кроме центрального бина,
характеризуются нулевым спектром. Если
входная последовательность ДПФ имеет
ровно k полных периодов (т.е. центральная
частота ее спектра точно совпадает с
бином
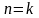 ),
то утечки не происходит. В этом случае
выражение (11) для всех
),
то утечки не происходит. В этом случае
выражение (11) для всех
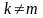 равно 0, а при
нормированное значение выражения (11)
равно 1.
равно 0, а при
нормированное значение выражения (11)
равно 1.
На рис.5.2 представлен
второй вариант, -
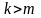 .
Этот график показывает, как будет
распределяться утечка спектра, если
анализируемые частоты не будут совпадать
ни с одной частотой
,
определяемой выражением (10).
.
Этот график показывает, как будет
распределяться утечка спектра, если
анализируемые частоты не будут совпадать
ни с одной частотой
,
определяемой выражением (10).
Предположим, что синусоида с частотой 8000 Гц., амплитуда которой равна единице, дискретизирована с частотой =32000 отсчетов/с.. Если вычислить 32-точечное ДПФ этой последовательности, то разрешение по частоте или интервал между бинами составит =32000/32=1000 Гц. Можно предсказать, что все частоты от 1000 Гц. до 32000 Гц. с дискретностью 1000 гц. будут определяться точно. Эффект растекания спектра для этих частот будет отсуствовать. Все частоты не попадающие в указанную сетку будут испытывать эффект растекания спектра, определяемый выражением(11).
Эффект растекания спектра рассмотрен в Программе 5
Программа 5 (fur_l_05.m).
N=32;
n=0:1:31;
t=1/32000;
x=sin(2*pi*8000*n*t);
y=fft(x);
xp=fftshift(y)
f=-N/2:1:(N/2-1)
a=abs(xp)/16
figure(1)
stem(f,a),grid on
x2=sin(2*pi*8500*n*t);
y2=fft(x2);
xp2=fftshift(y2)
a2=abs(xp2)/16
figure(2)
stem(f,a2),grid on
Результаты выполнения программы представлены на рис.6 и рис.7.
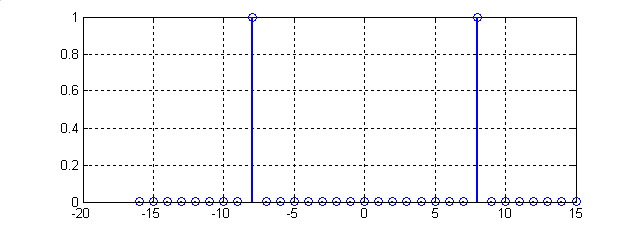
Рис.6. Частотный отклик ДПФ на входную последовательность 8 кГц.
Так как выполняется условие , то входная последовательность определяется точно и утечки спектра не наблюдается (рис.6). На рис.7 представлен вариант, иллюстрирующий утечку спектра, возникающего при частоте входного сигнала 8.5 кГц.
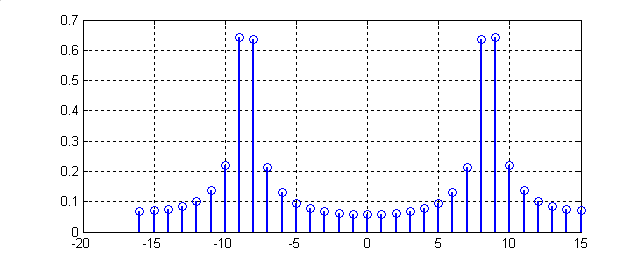
Рис.7. Частотный отклик ДПФ на входную последовательность 8.5 кГц.
Кривая на рис.7 показывает, как анализируемая частота, не кратная гармонике (не кратная бину), растекается (проявляется в спектре) всех гармоник. Так как частота 8.5 кГц расположена, с учетом разрешающей способности, симметрично между 8 и 9 бимном, то растекание между этими бинами происходит "почти" симметрично. При более глубоком рассмотрении ДПФ можно объяснить указанную несимметрию, но это выходит за рамки данной лабораторной работы. В этой работе обратим внимание, что приближение частоты к бину увеличивает его амплитуду. Причем, чем ближе анализируемая частота к частотам дискретного спектра, тем слабее эффект растекания. Можно предположить, что если бы анализировалась частота 8.75 кГц, то амплитуда 9 гармоники была бы больше, чем 7 гармоники. При приближении анализируемой частоты к частотам, кратным разрешающей способности ДПФ, растекание уменьшается и, при совпадении анализируемой частоты с одним из бинов, растекание прекращается совсем.
