19

8 Вопрос

Языки описания выбора. Процедуры выбора при критериальном описании: скалярно-оптимизационный механизм выбора, человеко-машинные процедуры, мажоритарные схемы.

Важнейшей операцией, обязательно входящей в любой целенаправленный процесс, является выбор. Он возникает в тот момент, когда появляется вариантность дальнейших действий по достижению цели. Естественно стремление понять, какой вариант действий следует принять, что такое “хороший выбор”, выработать рекомендации, как приблизиться к наилучшему выбору.

Как любая теория, теория выбора начинается с языка описания. К настоящему времени сложилось три основных языка описания выбора:

- критериальный язык;

- язык бинарных отношений;

- язык функций выбора.

Каждый следующий из названных языков является определенным обобщением предыдущего.

Критериальный язык. Это описание выбора является самым простым, наиболее развитым и чаще других употребляемым в приложениях. Его название связано с основным предположением, что каждую альтернативу (способ действия) можно оценить конкретным числом – значением критерия, и сравнение альтернатив свести к сравнению соответствующих чисел.

Пусть х – некоторая альтернатива из множества Х. Считается, что для всех хХ может быть задана функция q(x), которая называется критерием (критерием качества или эффективности, целевой функцией и т. д.) и обладает тем свойством, что если альтернатива х¹ предпочтительней альтернативы х², то q(x¹) < q(x²) (или q(x¹) > q(x²) в зависимости от физического смысла q(x)) и обратно.

Если теперь сделать еще одно предположение, что выбор любой альтернативы х приводит к однозначно известным последствиям (детерминированный выбор или выбор в условиях определенности), и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей альтернативой х* является, естественно, та, которая обладает экстремальным значением критерия:

x* = arg extr (q(x) | xX).

Задача выбора существенно усложняется, если критериев несколько.

Наличие многокритериальности связано с тем, что, как всякая модель, цель отражает объект моделирования лишь приближенно. Таким образом, многокритериальность появляется при стремлении увеличить степень адекватности модели, описать цель как можно более разнообразными средствами, дополняющими друг друга. Важно понять, что дело не только и не столько в количестве критериев, сколько в том, чтобы они достаточно полно “покрывали” цель. Это означает, что критерии должны описывать по возможности все важные аспекты цели, но при этом их число желательно минимизировать.

Теоретически можно представить случай, когда во множестве Х найдется одна альтернатива, для которой все критерии принимают наилучшие значения (максимальные или минимальные в зависимости от содержания задачи). Естественно, что данная альтернатива и будет наилучшей. К сожалению, на практике такие ситуации практически не встречаются, а типичным является случай, представленный на рис. 1.3, для двух целевых функций. При х =Х* максимума достигает одна целевая функция, а при х = Х** – другая; нам же предстоит сделать только один выбор.

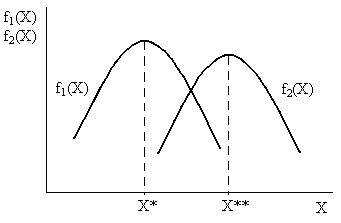
Рис. 1.3. Ситуация ПР при двух критериях

Язык бинарных отношений базируется на понятии бинарного отношения. Бинарным отношением между элементами множеств А и В называется любое подмножество упорядоченных пар R = {a, b}, a A, b B (R – от английского слова relation – отношение). Если множества A и B совпадают, А = В, то R называют бинарным отношением на множестве А. Если (x, y)R, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R.

В теории выбора и принятия решений большую роль играют бинарные отношения предпочтения, то есть такие отношения, согласно которым в паре (x, y)R элемент x в каком-то смысле лучше, чем y. Большая, нежели у критериального языка общность языка бинарных отношений основана на учете того факта, что в реальности дать оценку отдельно взятой альтернативе часто затруднительно или невозможно. Однако, если рассматривать ее не в отдельности, а в паре с другой альтернативой, то найдутся основания сказать, какая из них более предпочтительна.

Язык функций выбора. Некоторые особенности выбора привели к построению третьего, еще более общего языка его описания – функций выбора. Во-первых, нередко приходится сталкиваться с ситуациями, когда предпочтение между двумя альтернативами зависит от прочих альтернатив. Например, предпочтение покупателя между чайником и кофеваркой может зависеть от наличия в продаже кофемолки. Во-вторых, возможны такие ситуации выбора, когда понятие предпочтения вообще лишено смысла. Например, по отношению к множеству альтернатив довольно обычными являются процедуры выбора “типичного” или “среднего” представителя, теряющие смысл при выборе из двух альтернатив.