Функция тока.

Не делая пока предположения об отсутствии вихрей в жидкости, можно показать, что уже одно уравнение нераз­рывности налагает на поле скоростей условие, поддающееся и плоском движений простому кинематическому истолкованию. В самом деле, ура­внение неразрывности даст для несжимаемой жидкости

или иначе .

Если взять дифференциальное уравнение линий тока

или

то уравнение неразрывности (2.1) показывает, что левая часть по­следнего уравнения представляет собой полный дифференциал неко­торой функции ψ

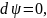
так что

Функция ψ(x,y) носит название функции тока,так как на каждой линии тока она сохраняет свое постоянное значение ψ(x,y)=С, различное вообще для различных линий тока.

Если между двумя точками A(x_1,у1) и B{x₂, у₂) провести неко­торую кривую (рис. 2.1), то нетрудно усмотреть, что поток жидкости через эту кривую выразится разностью значений функций тока в точках AиВ,независимо от формы кривой.

Поток жидкости через кривую

Связь функции тока с потенциалом скорости.

При суще­ствовании в плоском движении потенциала скорости φ будут иметь место равенства

Сравнивая которые с (2.2), устанавливаем

или иначе:

Последнее соотношение показывает, что каждая кривая семейства φ=const, пересекается под прямым углом с любой кривой семейства линий ψ = const, иначе говоря, линии тока являются ортогональными траекториями семейства изопотенциальных линий. Всякая определен­ная форма плоского движения жидкости интерпретируется определенной картиной распределения кривых φ = const, и ψ = const в плоскости. В силу взаимной ортогональности кривых этих семейств является безразличным с геометрической точки зрения, какие из них принять за линии тока, а какие за изопотенциальные кривые. На этом осно­вании функции φ и ψ называются сопряженными,и мы приходим к заключению, что если удастся найти решение некоторой определенной плоской гидродинамической задачи, т. е. если удастся подобрать потенциал скорости φ(а значит, н функцию тока ψ) так, чтобы поле скоростей удовлетворяло определенным пограничным условиям, то мы одновременно получаем решение другой плоской задачи, в которой — ψ будет служить потенциалом, а φ— функцией тока.

Комплексная скорость и комплексный потенциал.

Усло­вия (3.2), выражающие связь между сопряженными функциями φ и ψ, суть не что иное, как известные условия Коши — Римана, выражающие то обстоятельство, что комплексное выражение ω=φ+ψi является аналитическойфункцией комплексного аргумента z=x+yi.

ω=f(z); φ+ψi=f(x+yi),

т. e. что функция f(z) будет иметь определенную производную

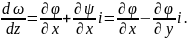
Последняя формула показывает, что производная dω/dzтесно связана со скоростью

.

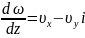Если рассматривать вещественную единицу +1 и мнимую еди­ницу i как единичные векторы (орты), отложенные по осямОхиОу,то комплексное число может быть изображено вектором скорости, отложенным от начала координат (рис. 4.1); сопря­женное же число изобразится вектором v.

Вектор скорости, отложенный от начала координат

Который служит зеркальным отражением вектора скорости по отношению к вещественной осиОх. На этом основании комплексное число dw/dzносит название комплексной скорости; модуль комплексной скорости дает величину скорости:

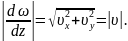
Функция ω=φ+ψi носит название комплексного потенциала.

Заметим, что если в (4.1) рассматривать zкак обратную функцию комплексного потенциала ω:

z=F(ω); x+yi=F(φ+ψi)

то производная этой функции dz/dωизобразит вектор, одинаковонаправленный со скоростью 𝜐 и имеющий длину 1/ в самом деле: