
- •Тема №1
- •Тема №2
- •Тема № 3.
- •Тема № 4
- •Связь функции тока с потенциалом скорости
- •Комплексная скорость и комплексный потенциал
- •Тема № 5
- •Функция тока.
- •Связь функции тока с потенциалом скорости.
- •Комплексная скорость и комплексный потенциал.
- •Подъёмная сила .
- •Тема №6
- •Гипотеза о пограничном слое.
- •Тема №7
Тема № 3.
П-теорема
Наименование раздела |
Содержание раздела |
|
Общая интегральная форма уравнений количества движения и момента количества движения (частные случаи). Подобие гидромеханических процессов. Теория физического подобия |
Теория размерности формулы Фурье. Определяющие параметры, π-теорема подобия. Критерии подобия и моделирования. Роль подобия в теоретических и экспериментальных исследованиях. |
|
π -теорема — основополагающая теорема анализа размерностей. Она позволяет вычислять множество безразмерных величин по данным физическим значениям, даже если неизвестно выражение, связывающее эти значения. Способ выбора множества безразмерных параметров не единственный: π -теорема демонстрирует, как это можно сделать, но не обеспечивает, что полученные параметры будут наиболее «физически значимыми».
Теория размерности
Теория размерности — часть общей топологии, в которой изучаются размерности — числовые топологические инварианты определённого типа. Размерность определяются тем или иным естественным образом на широком классе топологических пространств. При этом, если X есть полиэдр (в частности, многообразие) размерность Xсовпадает с числом измерений в смысле элементарной геометрии.
История
Первое общее определение размерности (большой индукционной размерности Ind) было дано Брауэром (1913), оно основывалось на идее Пуанкаре. В 1921 Менгер и Урысон независимо от Брауэра и друг от друга пришли к похожему определению (так называемая малая индуктивная размерность ind). Наиболее общее определение размерности дал Хаусдорф в 1919 году (см. Размерность Хаусдорфа) Совершенно иной подход к понятию размерности берёт начало от Лебега.
Формулы Фурье
Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Преобразование
Фурье функции
![]() вещественной
переменной является интегральным
преобразованием и задается следующей
формулой:
вещественной
переменной является интегральным
преобразованием и задается следующей
формулой:
f(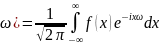
Отметим, что разные источники могут давать определения, отличающиеся от приведенного выбором коэффициента перед интегралом, а также знака «−» в показателе экспоненты. Все свойства в этом случае будут аналогичны, хотя вид каких-то формул может измениться.
Применения преобразования Фурье
Преобразование Фурье используется во многих областях науки — в физике, теории чисел, комбинаторике, обработке сигналов, теории вероятностей, статистике, криптографии, акустике, океанологии, оптике, геометрии, и многих других. В обработке сигналов и связанных областях преобразование Фурье обычно рассматривается как декомпозиция сигнала на частоты и амплитуды, то есть, обратимый переход от временно́го пространства (timedomain) в частотное пространство (frequencydomain). Богатые возможности применения основываются на нескольких полезных свойствах преобразования:
Преобразования являются линейными операторами и, с соответствующей нормализацией, также являются унитарными (свойство, известное как теорема Парсеваля или, в более общем случае как теорема Планшереля, или в наиболее общем как дуализм Понтрягина).
Преобразования обратимы, причём обратное преобразование имеет практически такую же форму, как и прямое преобразование.
Синусоидальные базисные функции (вернее, комплексные экспоненты) являются собственными функциями дифференцирования, что означает, что данное представление превращает линейные дифференциальные уравнения с постоянными коэффициентами в обычные алгебраические. (Например, в линейной стационарной системе частота — консервативная величина, поэтому поведение на каждой частоте может решаться независимо.)
По теореме о свёртке, преобразование Фурье превращает сложную операцию свёртки в простое умножение, что означает, что они обеспечивают эффективный способ вычисления основанных на свёртке операций, таких как умножение многочленов и умножение больших чисел.
Дискретная версия преобразования Фурье может быстро рассчитываться на компьютерах, используя алгоритм быстрого преобразования Фурье (БПФ, англ. FFT).
Таблица важных преобразований Фурье
Следующая
таблица содержит список важных формул
для преобразования Фурье F(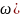 и G(
обозначают фурье компоненты функций
f(t)
и g(t),
соответственно.f
и g
должны быть интегрируемыми функциями
или обобщёнными
функциями.
и G(
обозначают фурье компоненты функций
f(t)
и g(t),
соответственно.f
и g
должны быть интегрируемыми функциями
или обобщёнными
функциями.
Помните,
что соотношения в этой таблице и в
особенности множители такие как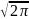 ,
зависят
от соглашения,
какая форма определения для Фурье
преобразования использовалась прежде
(хотя в общем виде соотношения, конечно,
правильны).
,
зависят
от соглашения,
какая форма определения для Фурье
преобразования использовалась прежде
(хотя в общем виде соотношения, конечно,
правильны).
|
Функция |
Образ |
Примечания |
1 |
af(t)+bg(t) |
aF( |
Линейность |
2 |
F(t-a) |
e-iωaF(ω) |
Запаздывание |
3 |
eiat f(t) |
F(ω-a) |
Частотный сдвиг |
4 |
F(at) |
∣a∣-1F(ω/a) |
Если
∣a∣-1F(ω/a) становится плоским |
5 |
Dnf(t)/dtn |
(iω)nF(ω) |
Свойство преобразования Фурье от n-й производной |
6 |
tnf(t) |
iIndnF(ω)/d ωn |
Это обращение правила 5 |
7 |
(f *g)(t) |
F(ω)G(ω) |
Запись f *g означает свёртку f иg. Это правило — теорема о свёртке |
8 |
f(t)g(t) |
(F*G) (ω)/ |
Это обращение 7 |
9 |
δ(t) |
1/ |
δ(t) означает дельта- функцию Дирака |
10 |
1 |
δ(ω) |
Обращение 9. |
11 |
tn |
in δ(n)(ω) |
Здесь, n — натуральное число, δ(ω) —-я обобщённая производная дельта- функции Дирака. Следствие правил 6 и 10. Использование его вместе с правилом 1 позволяет делать преобразования любых многочленов |
12 |
aiat |
δ(ω-a) |
Следствие 3 и 10 |
13 |
cos(at) |
|
Следствие 1 и 12 с использованием формулы Эйлера cos(at)=1(eiat+ e-iat/2 |
14 |
sin(at) |
δ(ω-a)+ δ(ω+a)/2i |
Также из 1 и 12 |
15 |
exp(-at2) |
1/ exp(-ω2/4a) |
Показывает, что функция Гаусса exp(-t2/2) совпадает со своим изображением |
16 |
W sinc(Wt) |
rect(ω/2W) |
Прямоугольная функция — идеальный фильтр низких частот и функция sinc(x) — её временной эквивалент |
17 |
1/t |
-i sgn(ω) |
Здесь sgn(ω)— sign функция. Это правило согласуется с 6 и 10 |
18 |
1/tn |
-i |
Обобщение 17 |
19 |
sgn(t) |
(iω)-1 |
Обращение 17 |
20 |
H(t) |
1/iω+π δ(ω) |
Здесь H(t)— функция Хевисайда. Следует из правил 1 и 19 |
П-теорема
Рассмотрим зависимость
q =f (l,t,m,υ,p,…,ω),
(1)
которая выражает функциональную связь между размерной величиной q и размерными независящими одна от другой величинами l,t,m….
Установим общую структуру функции f (l,t…), предполагая, что ею выражается некоторый физический (в частности, гидро- динамический) закон. Допустим, что из числа величин l,t,m…, ω,a, p, υ первые три, т. е. l,t,m, имеют независимые размерности, т. е. формула размерности любой из этих величин не может быть представлена как комбинация формул размерности двух других. (В качестве величин l,t,m с независимыми размерностями могут быть взяты не обязательно величины с простыми размерностями, как, например, длина, время и масса. Вместо времени может быть взята скорость или ускорение, вместо массы — плотность, вместо длины — произведение скорости на время и т. п.).
Заметим, что все нижеследующие рассуждения остаются справедливыми и в том случае, если величин с независимыми размерностями будет не три, а сколько угодно.
Если величинами l,t,m, которые условимся называть основ- ными, исчерпывается число величин с независимыми размер- ностями, то размерности остальных величин ω,a,p,…υ можно выразить через размерности величин l,t,m. Так, если L, T и M соответственно единицы измерения для l,t,m, то формулами размерности будут
[l] = L; [t] = Т; [т] = М
(2)
[υ] = LxυTyυMzυ ; [a]= LхТуаМzа...
(3)
Изменим теперь единицы измерения основных величин соот- ветственно в αl, αt, и αm раз, т. е. перейдем к единицам
L1 = αlL; T1 = αt T ; M1 = αm M.
(4)
Тогда величины q, l,t,m, υ ,a... в уравнении (1) будут выражаться в этих новых единицах, но вид уравнения не должен измениться, так как оно выражает, по предположению, некоторый физический закон, который не может зависеть от выбора системы единиц. Поэтому в новых единицах вместо (1) можем написать:
q1 =f 1(l1,t1,m1,υ1,…,n1),
(5)
Величины q1,l1,…,n1 выраженные в новых единицах L1 ,T1 ,M1, связаны с их значениями в старых единицах соотношениями
l1 = αll; t1 = αt t; m1 = αm m.
(6)
q1=α l xq * α t yq * α m zq * q, υ1= α l xυ * α t yυ * α m zυ * υ…
(7)
Выражение (5) можно переписать в виде:
q * α l xq * α t yq * α m zq =f (αll, αtt, αm m, α l xυ * α t yυ * α m zυ ,…).
(8)
Поскольку линейные масштабы единиц измерения основных величин αl, αt, αm произвольны, то, в частности, их можно выбрать так, чтобы
αl=
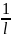 ;
αt=
;
αt=
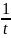 ;
αm=
;
αm=
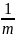 .
.
(9)
При таком выборе масштабов αl , αt ,αm мы, фактически, за единицы измерения принимаем основные величины l,t,m, входящие в уравнение (1). Тогда последняя форма исходного уравнения перейдет в следующую:
q υ a
 =
f
(1,1,1, , …).
=
f
(1,1,1, , …).
l xq* t yq * m zq l xυ* t yυ * m zυ l xa* t ya * m za
(10)
Входящие в это уравнение комплексы:
υ a
, …
l xυ* t yυ * m zυ l xa* t ya * m za
(11)
являются, очевидно, безразмерными. Вводя для них соответствующие обозначения πq, πυ, πa ..., приходим к уравнению:
πq =f (1,1,1, πυ, πa, …, πω)
(12)
или, в более компактной записи, — к уравнению
φ (πq, πυ, πa ,... ,πω) = 0.
(13)
Обобщая полученный результат на произвольное число величин, входящих в исходное уравнение (1), можно сформулировать следующую теорему.
Выражающая некоторый физический закон функциональная
связь между n= k + s размерными величинами (l,t,m,
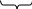
k
q,ω,a,p,…υ ), из которых k величин l,t,m…имеют независимые s
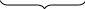
размерности, может быть представлена в виде связи между n—k = s безразмерными комплексами πq, πυ,… πω, каждый из которых является комбинацией из k + 1 размерных величин.
Эта теорема, получившая название π-теоремы, является основной в теории размерностей и в то же время входит в число трех основных теорем теории подобия. Ее роль в теории подобия определяется тем, что безразмерные комплексы πi, представляют собой критерии подобия, и, следовательно, уравнение (12) дает связь между ними.
Критерий подобия
Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем.
Критерии подобия, представляющие собой отношения одноимённых физических параметров системы (например, отношения длин), называются тривиальными и при установлении определяющих критериев подобия обычно не рассматриваются: равенство их для двух систем является определением физического подобия. Нетривиальные безразмерные комбинации, которые можно составить из определяющих параметров, и представляют собой критерии подобия.
Всякая новая комбинация из критериев подобия также является критерием подобия, что даёт возможность в каждом конкретном случае выбрать наиболее удобные и характерные критерии. Число определяющих нетривиальных критериев подобия меньше числа определяющих физических параметров с различными размерностями на величину, равную числу определяющих параметров с независимыми размерностями.
Если известны уравнения, описывающие рассматриваемое физическое явление, то критерии подобия для этого явления можно получить, приводя уравнения к безразмерному виду путём введения некоторых характерных значений для каждого из определяющих физических параметров, входящих в систему уравнений. Тогда критерии подобия определятся как безразмерные коэффициенты, появляющиеся перед некоторыми из членов новой, безразмерной системы уравнений. Когда уравнения, описывающие физическое явление, неизвестны, критерии подобия отыскиваются при помощи анализа размерностей, определяющих физические параметры.
В гидромеханике важнейшими критериями подобия являются:
Число Рейнольдса:

Определяет, в частности, переход от ламинарного режима к турбулентному.
Число Маха:
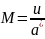 .
.
Число Фруда:
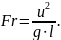
В этих примерах
g — плотность жидкости или газа,
l — характерный размер,
u — скорость течения,
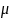 — динамический
коэффициент вязкости,
— динамический
коэффициент вязкости,
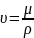 — кинематический
коэффициент вязкости ,
— кинематический
коэффициент вязкости ,
a* — местная скорость распространения звука в движущейся среде.
Каждый
из критериев подобия имеет определенный
физический смысл как величина,
пропорциональная отношению однотипных
физических величин. Так, число
![]() характеризует
отношение инерционных сил при движении
жидкости или газа к силам вязкости, а
число
характеризует
отношение инерционных сил при движении
жидкости или газа к силам вязкости, а
число
![]() —
отношение инерционных сил к силам
тяжести.
—
отношение инерционных сил к силам
тяжести.
Основными критериями подобия процессов теплопередачи между жидкостью (газом) и обтекаемым телом являются
число
Прандтля
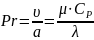 ,
,
число
Нуссельта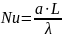 ,
,
число
Грасгофа
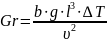 ,
,
а
также число
Пекле
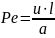 и
и
число
Стэнтона
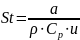 .
.
Здесь
a —
коэффициент
теплоотдачи, 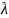 — коэффициент теплопроводности,
— коэффициент теплопроводности, 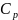 —
удельная
теплоёмкость
жидкости или газа при постоянном
давлении, a=
—
удельная
теплоёмкость
жидкости или газа при постоянном
давлении, a=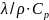 —
коэффициент
температуропроводности,
b — коэффициент
объёмного расширения,
—
коэффициент
температуропроводности,
b — коэффициент
объёмного расширения,
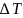 —
разность температур поверхности тела
и жидкости (газа). Два последних числа
связаны с предыдущими соотношениями:
Ре = Pr×Re, St = Nu/Pe.
—
разность температур поверхности тела
и жидкости (газа). Два последних числа
связаны с предыдущими соотношениями:
Ре = Pr×Re, St = Nu/Pe.
Физическое моделирование
Физи́ческое модели́рование — метод экспериментального изучения различных физических явлений, основанный на их физическом подобии. Метод применяется при следующих условиях:
Исчерпывающе точного математического описания явления на данном уровне развития науки не существует, или такое описание слишком громоздко и требует для расчётов большого объёма исходных данных, получение которых затруднительно.
Воспроизведение исследуемого физического явления в целях эксперимента в реальных масштабах невозможно, нежелательно или слишком дорогостояще (например, цунами).
Метод состоит в создании лабораторной физической модели явления в уменьшенных масштабах, и проведении экспериментов на этой модели. Выводы и данные, полученные в этих экспериментах, распространяются затем на явление в реальных масштабах. Метод может дать надёжные результаты, лишь в случае соблюдения физического подобия реального явления и модели. Подобие достигается за счёт равенства для модели и реального явления значений критериев подобия — безразмерных чисел, зависящих от физических (в том числе геометрических) параметров, характеризующих явление. Экспериментальные данные, полученные методом физического моделирования распространяются на реальное явление также с учётом критериев подобия.
В широком смысле, любой лабораторный физический эксперимент является моделированием, поскольку в эксперименте наблюдается конкретный случай явления в частных условиях, а требуется получить общие закономерности для всего класса подобных явлений в широком диапазоне условий. Искусство экспериментатора заключается в достижении физического подобия между явлением, наблюдаемым в лабораторных условиях и всем классом изучаемых явлений.
Некоторые примеры применения метода физического моделирования:
Исследование течений газов и обтекания летательных аппаратов, автомобилей, и т. п. в аэродинамических трубах.
Гидродинамические исследования на уменьшенных моделях кораблей, гидротехнических сооружений и т. п.
Исследование сейсмоустойчивости зданий и сооружений на этапе проектирования.
Изучение устойчивости сложных конструкций, под воздействием сложных силовых нагрузок.
Измерение тепловых потоков и рассеивания тепла в устройствах и системах, работающих в условиях больших тепловых нагрузок.
Изучение стихийных явлений и их последствий.

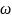 )+bG
)+bG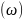
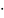 δ(ω-a)+
δ(ω+a)/2
δ(ω-a)+
δ(ω+a)/2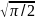 (-iω)n-1sgn
(ω)/(n-1)!
(-iω)n-1sgn
(ω)/(n-1)!