7. Обработка результатов эксперимента. Метод наименьших квадратов.

Для правильной интерпретации результатов, используют различные статистические методы обработки данных. Одним из наиболее известных является метод наименьших квадратов.

Суть метода – на имеющемся поле распределения случайной величины необходимо найти уравнение линии минимально удаленной от всех экспериментальных точек.

Проблема заключается в том, что одни точки лежат выше необходимой линии, а другие – ниже, и простое суммирование дает в результате ноль.

Для решения этой проблемы суммируют квадраты этих расстояний.

Д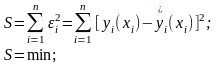 ля того, чтобы разброс был минимальным необходимо выполнение условия:

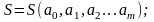
Очевидно, что

Тогда получим m уравнений вида

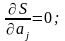
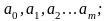
из которых определим

Уравнений получится столько, сколько неизвестных коэффициентов необходимо определить.

Рассмотрим применение метода наименьших квадратов для линейной модели.

Пусть имеем набор экспериментальных данных вида:

Сумма квадратов отклонений от «истинной» прямой

8. Проверка адекватности модели. Проверка значимости коэффициентов.

Проверка адекватности модели

После вычисления коэффициентов необходимо провести проверку модели. Такую проверку называют проверкой адекватности моделей. Рассмотрим два случая с одинаковым расположением экспериментальных точек. В обоих случаях одинаковый разброс относительно линии регрессии. Единственное различие в этих вариантах у нас будет разный разброс в точках, т.е. разная дисперсия воспроизводимости. Разброс в точках обозначают отрезками прямых, которые составляют доверительный интервал ± 2S{y} . Линия регрессии лежит внутри доверительных интервалов для каждой точки. Разброс в точках того же порядка, что и разброс относительно лини, поэтому можно считать, что модель пригодна. Во 2-м случае опыты проведены слишком точно и линии регрессии пересекают не все доверительные интервалы, такая модель не пригодна и ее нужно как-то преобразовывать, но это качественные соображения, а не количественные. Для характеристики среднего разброса относительно линии регрессии можно использовать остаточную сумму квадратов. Единственное неудобство заключается в том, что эта сумма зависит от числа коэффициентов в уравнении. Поэтому ее относят на один свободный опыт. Число таких опытов, или число степеней свободы определяется как разность между числом опытов и числом коэффициентов. F=N-(k+1). Остаточная сума квадратов деленная на число степеней свободы называется остаточной дисперсией или дисперсией адекватности.

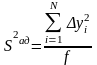
Для проверки гипотезы об адекватности можно использовать f-критерий 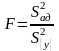. Эта величина сравнивается с табличными данными. Столбцы таблицы Фишера, связаны с числом степеней свободы числителя, а строки для знаменателя. На пересечении находятся значения f - критерий. Если расчетные значения не превышает табличных, то модель можно считать адекватной.

Проверка значимости коэффициентов

Проверка значимости каждого коэффициента проводится независимо, ее можно осуществлять двумя способами: 1-й способ это по t-критерию Стьюдента, 2-й - построение доверительного интервала. Для полного факторного эксперимента и дробных реплик доверительные интервалы для всех коэффициентов равны друг другу. Прежде всего, надо найти дисперсию коэффициента регрессии:

Доверительный интервал строится следующим образом 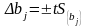. Коэффициент значим, если его абсолютная величина больше доверительного интервала. Доверительный интервал задается верхней и нижней границей: bj + Δbj , bj - Δbj. В действительности, чем уже доверительный интервал, тем более значимым является коэффициент. При проверке по t – критерию используют следующую формулу:

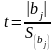
Вычисленное значение t – критерия сравнивают с табличным.

Незначимые коэффициенты из модели исключаются.